1561:, arguing that Cauchy's proof had to be incorrect. Completely standard notions of convergence did not exist at the time, and Cauchy handled convergence using infinitesimal methods. When put into the modern language, what Cauchy proved is that a uniformly convergent sequence of continuous functions has a continuous limit. The failure of a merely pointwise-convergent limit of continuous functions to converge to a continuous function illustrates the importance of distinguishing between different types of convergence when handling sequences of functions.
9070:
12793:
196:
20:
13102:
2359:
8675:
10756:
or even to any function at all. In order to ensure a connection between the limit of a sequence of differentiable functions and the limit of the sequence of derivatives, the uniform convergence of the sequence of derivatives plus the convergence of the sequence of functions at at least one point is
10323:
of continuous functions. The erroneous claim that the pointwise limit of a sequence of continuous functions is continuous (originally stated in terms of convergent series of continuous functions) is infamously known as "Cauchy's wrong theorem". The uniform limit theorem shows that a stronger form
10318:
This theorem is an important one in the history of real and
Fourier analysis, since many 18th century mathematicians had the intuitive understanding that a sequence of continuous functions always converges to a continuous function. The image above shows a counterexample, and many discontinuous
11571:
functions converges uniformly in a region S of the complex plane, then the limit is analytic in S. This example demonstrates that complex functions are more well-behaved than real functions, since the uniform limit of analytic functions on a real interval need not even be differentiable (see
2177:
10242:
7172:
1719:
compares the three definitions in his paper "Sir George Stokes and the concept of uniform convergence" and remarks: "Weierstrass's discovery was the earliest, and he alone fully realized its far-reaching importance as one of the fundamental ideas of analysis."
5751:
8368:
9988:
8493:
9716:
8253:
2354:{\displaystyle f_{n}\rightrightarrows f,\quad {\underset {n\to \infty }{\mathrm {unif\ lim} }}f_{n}=f,\quad f_{n}{\overset {\mathrm {unif.} }{\longrightarrow }}f,\quad f=\mathrm {u} \!\!-\!\!\!\lim _{n\to \infty }f_{n}.}
11428:
In fact, for a uniformly convergent family of bounded functions on an interval, the upper and lower
Riemann integrals converge to the upper and lower Riemann integrals of the limit function. This follows because, for
2867:
1474:
The difference between uniform convergence and pointwise convergence was not fully appreciated early in the history of calculus, leading to instances of faulty reasoning. The concept, which was first formalized by
5508:
10002:
5273:
11423:
11151:
7410:
3406:
5355:
8054:
1639:
6152:
2967:
2428:
3331:
11718:
10884:
10596:
10696:
7003:
6576:
7503:
In this example one can easily see that pointwise convergence does not preserve differentiability or continuity. While each function of the sequence is smooth, that is to say that for all
2119:
476:
6822:
6074:
1469:
996:
10557:
8428:
3458:
3192:
3124:
2692:
1888:
1840:
8478:
7465:
11967:
11851:
7609:
9433:
7498:
12085:
11630:
11259:
8954:
7734:
4528:
12306:
7566:
7649:
4585:
258:
7820:
9073:
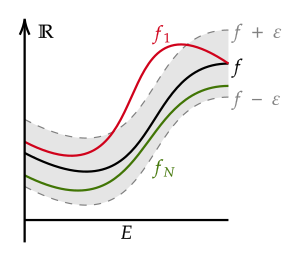
Counterexample to a strengthening of the uniform convergence theorem, in which pointwise convergence, rather than uniform convergence, is assumed. The continuous green functions
1946:
5618:
9606:
6995:
6698:
3744:
7258:
4378:
4129:
3224:
2585:
1138:
11526:
10471:. This is however in general not possible: even if the convergence is uniform, the limit function need not be differentiable (not even if the sequence consists of everywhere-
7890:
5923:
5866:
4318:
1975:
10313:
9207:
8774:
6735:
6641:
6419:
6007:
4002:
3910:
3875:
3716:
2738:
860:
12308:. In other words, almost uniform convergence means there are sets of arbitrarily small measure for which the sequence of functions converges uniformly on their complement.
10965:
4906:
4434:
3635:
12193:
11786:
9400:
9110:
5590:
4708:
3076:
2636:
2611:
12220:
10726:
10469:
8741:
7964:
7927:
4953:
4845:
4487:
9834:
9533:
6229:
5981:
4798:
3820:
3050:
2464:
10929:
8264:
7278:
6347:
6307:
6192:
4209:
4149:
4088:
4022:
1281:
1178:
880:
759:
516:
385:
161:
94:
10754:
4744:
1261:
710:
190:
12273:
12240:
12163:
10793:
10621:
10439:
9744:
9361:
9043:
8886:
7693:
6886:
6506:
6100:
5564:
5392:
5007:
3591:
2021:
1402:
1336:
929:
322:
54:
11877:
11744:
7846:
4068:
3943:
3797:
3558:
3532:
2534:
2047:
1682:
1097:
1023:
825:
11493:
11458:
11350:
11189:
11024:
10390:
10292:
9884:
9801:
9771:
9580:
9258:
8705:
8670:{\displaystyle \lim _{n\to \infty }{\frac {M_{n+1}}{M_{n}}}=\lim _{n\to \infty }{\frac {R^{n+1}}{R^{n}}}{\frac {n!}{(n+1)!}}=\lim _{n\to \infty }{\frac {R}{n+1}}=0}
8165:
8138:
8084:
7761:
7336:
7213:
6933:
6860:
6480:
6267:
5054:
4872:
4663:
4628:
3771:
3670:
2997:
2149:
1659:
1504:
1051:
634:
587:
141:
1310:
739:
11551:
Much stronger theorems in this respect, which require not much more than pointwise convergence, can be obtained if one abandons the
Riemann integral and uses the
5809:
5783:
5082:
4981:
12024:
9891:
8797:
8107:
6442:
11546:
11323:
11303:
11283:
11044:
10414:
10363:
10265:
9857:
9626:
9553:
9473:
9453:
9328:
9308:
9278:
9227:
9154:
9134:
9010:
8986:
8849:
7984:
7298:
6906:
6755:
6596:
6387:
6367:
6327:
6287:
6172:
5943:
5610:
5531:
5122:
5102:
5027:
4229:
4189:
4169:
4042:
3963:
3840:
3690:
3502:
3482:
3144:
3017:
2758:
2712:
2508:
2484:
2169:
1995:
1912:
1788:
1539:
1376:
1356:
1224:
1199:
1158:
1071:
902:
799:
779:
674:
654:
607:
560:
538:
496:
405:
365:
345:
114:
74:
12984:
11076:
10997:
10825:
1684:
While he thought it a "remarkable fact" when a series converged in this way, he did not give a formal definition, nor use the property in any of his proofs.
4231:
that are given. Thus uniform convergence implies pointwise convergence, however the converse is not true, as the example in the section below illustrates.
9633:
12512:
11356:
8173:
10479:), and even if it is differentiable, the derivative of the limit function need not be equal to the limit of the derivatives. Consider for instance
12627:
2766:
8824:
A sequence of continuous functions on metric spaces, with the image metric space being complete, is uniformly convergent if and only if it is
12974:
10237:{\displaystyle \forall x\in U\quad d(f(x),f(x_{0}))\leq d(f(x),f_{N}(x))+d(f_{N}(x),f_{N}(x_{0}))+d(f_{N}(x_{0}),f(x_{0}))\leq \varepsilon }
13067:
12599:
5399:
5159:
2171:
is not quite standardized and different authors have used a variety of symbols, including (in roughly decreasing order of popularity):
12908:
7344:
3342:
5292:
12348:
10337:
space, continuity is equivalent to local uniform continuity, and thus the uniform limit of continuous functions is continuous.
7996:
260:(marked in green and blue) converges pointwise over the entire domain, but the limit function is discontinuous (marked in red).
12918:
12452:
12418:
12469:
13136:
12320:
6105:
1575:
2879:
2370:
11081:
13141:
13082:
12913:
12673:
12620:
12343:
7167:{\displaystyle \left|f_{N}(x_{0})-f(x_{0})\right|=\left|\left^{N}-0\right|={\frac {1}{2}}>{\frac {1}{4}}=\epsilon ,}
3242:
11644:
10830:
10562:
13062:
12557:
12534:
12498:
6511:
13072:
12378:
Sørensen, Henrik Kragh (2005). "Exceptions and counterexamples: Understanding Abel's comment on Cauchy's
Theorem".
2054:
410:
6760:
6012:
1407:
934:
12964:
12954:
10482:
8376:
3415:
3149:
3081:
2649:
1845:
1797:
8435:
7418:
4750:
for a similar definition of uniform continuity). In contrast, pointwise continuity requires this only for real
10626:
10324:
of convergence, uniform convergence, is needed to ensure the preservation of continuity in the limit function.
9161:
7571:
12552:, Real Analysis: Modern Techniques and Their Applications, Second Edition, John Wiley & Sons, Inc., 1999,
11918:
11798:
9405:
7470:
13077:
12979:
12613:
12591:
12327:
11213:
8895:
7698:
4500:
3919:
Note that interchanging the order of quantifiers in the definition of uniform convergence by moving "for all
3637:
It is clear that uniform convergence implies local uniform convergence, which implies pointwise convergence.
12278:
12042:
11587:
7510:
13131:
13105:
7626:
5746:{\displaystyle f(x)=\lim _{n\to \infty }f_{n}(x)={\begin{cases}0,&x\in [0,1);\\1,&x=1.\end{cases}}}
4533:
202:
12358:
7766:
199:
The limit of a sequence of continuous functions does not have to be continuous: the sequence of functions
13087:
12586:
12581:
6195:
1917:
1572:, where he employed the phrase "convergence in a uniform way" when the "mode of convergence" of a series
9280:
is also well defined. The following result states that continuity is preserved by uniform convergence:
12969:
12311:
Note that almost uniform convergence of a sequence does not mean that the sequence converges uniformly
9585:
6938:
6646:
3721:
7218:
4323:
4093:
3200:
2539:
1102:
12959:
12949:
12939:
11498:
8825:
7851:
5871:
5814:
4262:
1951:
1708:
10297:
9167:
8746:
6703:
6601:
6398:
5986:
5680:
5408:
3972:
3880:
3845:
3695:
2717:
830:
4877:
4406:
3596:
12172:
11765:
9366:
9076:
8363:{\displaystyle \left|{\frac {z^{n}}{n!}}\right|\leq {\frac {|z|^{n}}{n!}}\leq {\frac {R^{n}}{n!}}}
5569:
4672:
3055:
2619:
2590:
13054:
12876:
12198:
8710:
4911:
4803:
4465:
12444:
9806:
9505:
9112:
converge to the non-continuous red function. This can happen only if convergence is not uniform.
7932:
7895:
6201:
5948:
4765:
3802:
3022:
2436:
12716:
12663:
12438:
12331:
10889:
7263:
6332:
6292:
6177:
4194:
4134:
4073:
4007:
1553:
published a proof that a convergent sum of continuous functions is always continuous, to which
1266:
1163:
865:
744:
501:
370:
289:
146:
79:
12406:
10934:
10623:
is also identically zero. However, the derivatives of the sequence of functions are given by
4713:
1230:
679:
166:
12923:
12668:
12245:
12225:
12135:
10765:
9723:
9487:), one uses the definitions of continuity and uniform convergence to produce 3 inequalities (
9333:
9064:
9015:
8858:
8818:
7665:
6865:
6485:
6079:
5536:
5364:
4986:
3966:
3563:
2639:
2487:
2000:
1712:
1550:
1381:
1315:
908:
294:
281:
269:
26:
11856:
11723:
11325:
is
Riemann integrable and its integral can be computed as the limit of the integrals of the
10701:
10444:
7825:
4047:
3922:
3776:
3537:
3511:
2513:
2026:
1727:
this concept and related questions were intensely studied at the end of the 19th century by
1664:
1076:
1002:
804:
13034:
12871:
12640:
11573:
11552:
11471:
11436:
11328:
11156:
11002:
10476:
10368:
10329:
10270:
9983:{\displaystyle \forall x\in U\quad d(f_{N}(x),f_{N}(x_{0}))\leq {\tfrac {\varepsilon }{3}}}
9862:
9779:
9749:
9558:
9236:
8811:
8683:
8143:
8116:
8062:
7739:
7620:
7303:
7180:
6911:
6827:
6447:
6234:
5032:
4850:
4641:
4606:
4452:
3749:
3648:
2975:
2127:
1752:
1732:
1644:
1482:
1029:
612:
565:
277:
119:
1286:
715:
8:
13014:
12316:
11564:
10731:
9994:
9492:
8480:
is convergent, then the M-test asserts that the original series is uniformly convergent.
5788:
5762:
5279:
5059:
4958:
1565:
1519:
1507:
11991:
10601:
10419:
8779:
8089:
6424:
5533:
pointwise but not uniformly. To show this, we first observe that the pointwise limit of
12944:
12855:
12840:
12812:
12792:
12731:
11531:
11308:
11288:
11268:
11029:
10399:
10348:
10250:
9842:
9611:
9538:
9458:
9438:
9313:
9293:
9263:
9212:
9139:
9119:
8995:
8971:
8834:
7969:
7652:
7283:
6891:
6740:
6581:
6372:
6352:
6312:
6272:
6157:
5928:
5595:
5516:
5107:
5087:
5012:
4214:
4174:
4154:
4027:
3969:
of the sequence. To make this difference explicit, in the case of uniform convergence,
3948:
3825:
3675:
3487:
3467:
3129:
3002:
2743:
2697:
2493:
2469:
2154:
1980:
1897:
1773:
1569:
1524:
1361:
1341:
1209:
1184:
1143:
1056:
887:
784:
764:
659:
639:
592:
545:
523:
481:
390:
350:
330:
99:
59:
12319:
does guarantee that on a finite measure space, a sequence of functions that converges
11049:
10970:
10798:
1541:
if the convergence is uniform, but not necessarily if the convergence is not uniform.
13126:
13044:
12845:
12817:
12771:
12761:
12741:
12726:
12553:
12530:
12494:
12448:
12414:
12353:
12312:
11568:
10472:
9157:
8989:
5128:
4800:, a basic example of uniform convergence can be illustrated as follows: the sequence
4384:
1791:
1554:
1515:
13029:
12850:
12776:
12766:
12746:
12648:
12522:
12387:
11202:
9711:{\displaystyle \forall x\in E\quad d(f_{N}(x),f(x))\leq {\tfrac {\varepsilon }{3}}}
5135:
4600:
2646:
can be used to give an equivalent alternative formulation for uniform convergence:
1724:
1688:
1511:
1476:
9483:
trick", and is the archetypal example of this trick: to prove a given inequality (
9069:
6389:
approaches 1. These observations preclude the possibility of uniform convergence.
1740:
12807:
12736:
10334:
4747:
2643:
1696:
13039:
13024:
13019:
12698:
12683:
12549:
10320:
9046:
5142:
4591:. In this situation, uniform limit of continuous functions remains continuous.
3195:
1728:
1558:
11201:
Similarly, one often wants to exchange integrals and limit processes. For the
8248:{\displaystyle \left|{\frac {z^{n}}{n!}}\right|\leq M_{n},\forall z\in D_{R}.}
1691:, who attended his course on elliptic functions in 1839–1840, coined the term
195:
13120:
13004:
12678:
12391:
12122:
11262:
8852:
8110:
5513:
is a classic example of a sequence of functions that converges to a function
5124:
are selected closer and closer to 1 (explained more in depth further below).
4400:
1760:
13009:
12751:
12693:
12539:
12486:
12434:
9230:
5283:
5150:
4256:
3505:
3228:
1756:
12756:
12703:
12504:
5138:
2862:{\displaystyle x\in E,m,n\geq N\implies |f_{m}(x)-f_{n}(x)|<\epsilon }
1736:
1716:
1707:, published in 1894. Independently, similar concepts were articulated by
265:
12605:
10393:
8988:
which is also continuous, then the convergence is necessarily uniform (
8484:
367:
as the function domain if, given any arbitrarily small positive number
2433:
to indicate that convergence is uniform. (In contrast, the expression
1755:, although the concept is readily generalized to functions mapping to
19:
12688:
8889:
12527:
Elements of
Mathematics: General Topology. Chapters 5–10 (paperback)
9720:(uniform convergence shows that the above statement is true for all
8807:
Every uniformly convergent sequence is locally uniformly convergent.
8707:
is convergent. Thus the original series converges uniformly for all
5503:{\displaystyle {\begin{cases}f_{n}:\to \\f_{n}(x)=x^{n}\end{cases}}}
12636:
9837:
9746:, but we will only use it for one function of the sequence, namely
5268:{\displaystyle d(f,g)=\|f-g\|_{\infty }=\sup _{x\in X}|f(x)-g(x)|.}
3233:
285:
12493:; Blackie and Son, London, 1954, reprinted by Dover Publications,
4090:
that is given. In contrast, in the case of pointwise convergence,
1842:
is a sequence of real-valued functions on it. We say the sequence
12407:"6.7 The Foundation of Analysis in the 19th Century: Weierstrass"
7990:
The complex exponential function can be expressed as the series:
2364:
Frequently, no special symbol is used, and authors simply write
6369:(which cannot be defined to be smaller) grows without bound as
11418:{\displaystyle \int _{I}f=\lim _{n\to \infty }\int _{I}f_{n}.}
10327:
More precisely, this theorem states that the uniform limit of
7623:
can be shown to be uniformly convergent on any bounded subset
10416:, it is often desirable to determine the derivative function
8113:. The Weierstrass M-test requires us to find an upper bound
7405:{\displaystyle \lim _{n\to \infty }\|f_{n}-f\|_{\infty }=1,}
3401:{\displaystyle f_{n}\rightrightarrows f\iff d(f_{n},f)\to 0}
11261:
is a sequence of
Riemann integrable functions defined on a
8821:
local uniform convergence and compact convergence coincide.
7177:
the candidate fails because we have found an example of an
5739:
5496:
5350:{\displaystyle \lim _{n\to \infty }\|f_{n}-f\|_{\infty }=0}
1479:, is important because several properties of the functions
8855:
interval (or in general a compact topological space), and
6194:(here the upper square brackets indicate rounding up, see
4239:
One may straightforwardly extend the concept to functions
1557:
in 1826 found purported counterexamples in the context of
12600:
Graphic examples of uniform convergence of
Fourier series
8049:{\displaystyle \sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.}
12509:
Sir George Stokes and the concept of uniform convergence
9608:. By uniform convergence, there exists a natural number
6578:
To see this, first observe that regardless of how large
4599:
Uniform convergence admits a simplified definition in a
1564:
The term uniform convergence was probably first used by
6395:
The convergence is not uniform, because we can find an
4383:
The most general setting is the uniform convergence of
12045:
11921:
11801:
11590:
11205:, this can be done if uniform convergence is assumed:
9969:
9697:
8394:
7935:
7898:
1634:{\textstyle \sum _{n=1}^{\infty }f_{n}(x,\phi ,\psi )}
1578:
12985:
1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ⋯ (inverses of primes)
12975:
1 − 1 + 2 − 6 + 24 − 120 + ⋯ (alternating factorials)
12281:
12248:
12228:
12201:
12175:
12138:
11994:
11859:
11768:
11726:
11647:
11534:
11501:
11474:
11439:
11359:
11331:
11311:
11291:
11271:
11216:
11159:
11084:
11052:
11032:
11005:
10973:
10937:
10892:
10833:
10801:
10768:
10734:
10704:
10629:
10604:
10565:
10485:
10447:
10422:
10402:
10371:
10351:
10300:
10273:
10253:
10005:
9894:
9865:
9845:
9809:
9782:
9752:
9726:
9636:
9614:
9588:
9561:
9541:
9508:
9461:
9441:
9408:
9369:
9336:
9316:
9296:
9266:
9239:
9215:
9170:
9142:
9122:
9079:
9018:
8998:
8974:
8898:
8861:
8837:
8782:
8749:
8713:
8686:
8496:
8438:
8379:
8267:
8176:
8146:
8119:
8092:
8065:
7999:
7972:
7854:
7828:
7769:
7742:
7701:
7668:
7629:
7574:
7513:
7473:
7421:
7347:
7306:
7286:
7266:
7221:
7183:
7006:
6941:
6914:
6894:
6868:
6830:
6763:
6743:
6706:
6649:
6604:
6584:
6514:
6488:
6450:
6427:
6401:
6375:
6355:
6335:
6315:
6295:
6275:
6237:
6204:
6180:
6160:
6147:{\displaystyle N=\lceil \log \epsilon /\log x\rceil }
6108:
6082:
6015:
5989:
5951:
5931:
5874:
5817:
5791:
5765:
5621:
5598:
5572:
5539:
5519:
5402:
5367:
5295:
5162:
5110:
5090:
5062:
5035:
5015:
4989:
4961:
4914:
4880:
4853:
4806:
4768:
4716:
4675:
4644:
4609:
4536:
4503:
4468:
4409:
4326:
4265:
4217:
4197:
4177:
4157:
4137:
4096:
4076:
4050:
4030:
4010:
3975:
3951:
3925:
3883:
3848:
3828:
3805:
3779:
3752:
3724:
3698:
3678:
3651:
3599:
3566:
3540:
3514:
3490:
3470:
3418:
3345:
3245:
3203:
3152:
3132:
3084:
3058:
3025:
3005:
2978:
2882:
2873:
In yet another equivalent formulation, if we define
2769:
2746:
2720:
2700:
2652:
2622:
2593:
2542:
2516:
2496:
2472:
2439:
2373:
2180:
2157:
2130:
2057:
2029:
2003:
1983:
1954:
1920:
1900:
1848:
1800:
1776:
1667:
1647:
1527:
1485:
1410:
1384:
1364:
1344:
1318:
1289:
1269:
1233:
1212:
1187:
1166:
1146:
1105:
1079:
1059:
1032:
1005:
937:
911:
890:
868:
833:
807:
787:
767:
747:
718:
682:
662:
642:
615:
595:
568:
548:
526:
504:
484:
413:
393:
373:
353:
333:
297:
205:
169:
149:
122:
102:
82:
62:
29:
4594:
2962:{\displaystyle d_{n}=\sup _{x\in E}|f_{n}(x)-f(x)|,}
2423:{\displaystyle f_{n}\to f\quad \mathrm {uniformly} }
11146:{\displaystyle f'(x)=\lim _{n\to \infty }f'_{n}(x)}
3078:. Thus, we can characterize uniform convergence of
827:in advance. In other words, there exists a number
676:in the following sense: in order to guarantee that
12513:Proceedings of the Cambridge Philosophical Society
12473:3rd edition, Theorem 7.17. McGraw-Hill: New York.
12300:
12267:
12234:
12214:
12187:
12157:
12079:
12018:
11961:
11871:
11845:
11780:
11738:
11712:
11624:
11540:
11520:
11487:
11452:
11417:
11344:
11317:
11297:
11277:
11253:
11183:
11145:
11070:
11038:
11018:
10991:
10959:
10923:
10878:
10819:
10787:
10748:
10720:
10690:
10615:
10590:
10551:
10463:
10433:
10408:
10384:
10357:
10307:
10286:
10259:
10236:
9982:
9878:
9851:
9828:
9795:
9765:
9738:
9710:
9620:
9600:
9574:
9547:
9527:
9467:
9447:
9427:
9394:
9355:
9322:
9302:
9272:
9252:
9221:
9201:
9148:
9128:
9104:
9037:
9004:
8980:
8948:
8880:
8843:
8791:
8768:
8735:
8699:
8669:
8472:
8422:
8362:
8247:
8159:
8132:
8101:
8078:
8048:
7978:
7958:
7921:
7884:
7840:
7814:
7755:
7728:
7687:
7643:
7603:
7560:
7492:
7459:
7404:
7330:
7292:
7272:
7252:
7207:
7166:
6989:
6927:
6900:
6880:
6854:
6816:
6749:
6729:
6692:
6635:
6590:
6570:
6500:
6474:
6436:
6413:
6381:
6361:
6341:
6321:
6301:
6281:
6261:
6223:
6186:
6166:
6146:
6094:
6068:
6001:
5975:
5937:
5917:
5860:
5803:
5777:
5745:
5604:
5584:
5558:
5525:
5502:
5386:
5349:
5267:
5116:
5096:
5076:
5048:
5021:
5001:
4975:
4947:
4900:
4866:
4839:
4792:
4738:
4702:
4657:
4622:
4579:
4522:
4481:
4428:
4372:
4312:
4223:
4203:
4183:
4163:
4143:
4123:
4082:
4062:
4036:
4016:
3996:
3957:
3937:
3904:
3869:
3834:
3814:
3791:
3765:
3738:
3710:
3684:
3664:
3629:
3585:
3552:
3526:
3496:
3476:
3452:
3400:
3325:
3218:
3186:
3138:
3118:
3070:
3044:
3011:
2991:
2961:
2861:
2752:
2732:
2706:
2686:
2630:
2605:
2579:
2528:
2502:
2478:
2458:
2422:
2353:
2163:
2143:
2113:
2041:
2015:
1989:
1969:
1940:
1906:
1882:
1834:
1782:
1676:
1653:
1633:
1533:
1498:
1463:
1396:
1370:
1350:
1330:
1304:
1275:
1255:
1218:
1193:
1172:
1152:
1132:
1091:
1065:
1045:
1017:
990:
923:
896:
874:
854:
819:
793:
773:
753:
733:
704:
668:
648:
628:
601:
581:
554:
532:
510:
490:
470:
399:
379:
359:
339:
316:
252:
184:
155:
135:
108:
88:
68:
48:
12323:also converges almost uniformly on the same set.
11884:With this definition comes the following result:
7763:be a sequence of positive real numbers such that
3326:{\displaystyle d(f,g)=\sup _{x\in E}|f(x)-g(x)|.}
2714:(in the previous sense) if and only if for every
2321:
2320:
2319:
2315:
2314:
801:, which we can find without knowing the value of
13118:
11713:{\displaystyle s_{n}(x)=\sum _{j=1}^{n}f_{j}(x)}
11377:
11106:
10879:{\displaystyle \lim _{n\to \infty }f_{n}(x_{0})}
10835:
10591:{\displaystyle f_{n}\rightrightarrows f\equiv 0}
8628:
8547:
8498:
7576:
7349:
5638:
5297:
5210:
3268:
2897:
2323:
12132:can be defined. We say a sequence of functions
8810:Every locally uniformly convergent sequence is
6888:. Explicitly, whatever candidate we choose for
6571:{\displaystyle |f_{n}(x)-f(x)|\geq \epsilon .}
5153:topology, with the uniform metric defined by
12621:
12315:as might be inferred from the name. However,
12116:
10795:is a sequence of differentiable functions on
8992:). Uniform convergence is also guaranteed if
8776:, the series is also uniformly convergent on
7215:that "escaped" our attempt to "confine" each
3945:" in front of "there exists a natural number
2114:{\displaystyle |f_{n}(x)-f(x)|<\epsilon .}
471:{\displaystyle f_{N},f_{N+1},f_{N+2},\ldots }
407:can be found such that each of the functions
13068:Hypergeometric function of a matrix argument
11641:if and only if the sequence of partial sums
11528:of the value of the upper and lower sums of
8059:Any bounded subset is a subset of some disc
7442:
7422:
7384:
7364:
6817:{\displaystyle |f_{n}(x)-f(x)|<\epsilon }
6141:
6115:
6069:{\displaystyle |f_{n}(x)-f(x)|<\epsilon }
5332:
5312:
5197:
5184:
4191:only has to work for the specific values of
1464:{\displaystyle |f_{n}(x)-f(x)|<\epsilon }
991:{\displaystyle |f_{n}(x)-f(x)|<\epsilon }
12924:1 + 1/2 + 1/3 + ... (Riemann zeta function)
10552:{\displaystyle f_{n}(x)=n^{-1/2}{\sin(nx)}}
8423:{\displaystyle M_{n}={\tfrac {R^{n}}{n!}}.}
6154:, which is the minimum integer exponent of
3453:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
3187:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
3119:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
2687:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
1883:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
1835:{\displaystyle (f_{n})_{n\in \mathbb {N} }}
12628:
12614:
10319:functions could, in fact, be written as a
9535:be an arbitrary point. We will prove that
8473:{\displaystyle \sum _{n=0}^{\infty }M_{n}}
7460:{\displaystyle \|f_{n}-f\|_{\infty }\to 0}
3366:
3362:
2801:
2797:
609:uniformly, then how quickly the functions
16:Mode of convergence of a function sequence
12980:1 + 1/2 + 1/3 + 1/4 + ⋯ (harmonic series)
12491:Theory and Application of Infinite Series
11962:{\textstyle f=\sum _{n=1}^{\infty }f_{n}}
11846:{\textstyle \sum _{n=1}^{\infty }|f_{n}|}
10691:{\displaystyle f'_{n}(x)=n^{1/2}\cos nx,}
10333:functions is uniformly continuous; for a
9160:, then it makes sense to talk about the
8167:independent of the position in the disc:
7722:
7637:
7604:{\displaystyle \lim _{n\to \infty }f_{n}}
3732:
3444:
3206:
3178:
3110:
2678:
2624:
1934:
1874:
1826:
12635:
12377:
11468:, and so the upper sum and lower sum of
9428:{\displaystyle f_{n}\rightrightarrows f}
9068:
7493:{\displaystyle f_{n}\rightrightarrows f}
2124:The notation for uniform convergence of
1751:We first define uniform convergence for
1026:. In contrast, pointwise convergence of
194:
18:
12443:. Cambridge University Press. pp.
12433:
12108:is equal to integral of the series of f
12080:{\textstyle \sum _{n=1}^{\infty }f_{n}}
11625:{\textstyle \sum _{n=1}^{\infty }f_{n}}
11254:{\displaystyle (f_{n})_{n=1}^{\infty }}
10340:
8949:{\displaystyle f_{n}(x)\leq f_{n+1}(x)}
7729:{\displaystyle f_{n}:E\to \mathbb {C} }
7614:
4523:{\displaystyle \alpha \geq \alpha _{0}}
1723:Under the influence of Weierstrass and
13119:
12404:
12349:Modes of convergence (annotated index)
12301:{\displaystyle E\setminus E_{\delta }}
9363:is a sequence of continuous functions
7966:converges absolutely and uniformly on
7561:{\displaystyle f_{n}\in C^{\infty }()}
6421:so that no matter how large we choose
5278:Then uniform convergence simply means
12609:
12242:such that the sequence of functions
11567:, one can show that if a sequence of
10365:is an interval and all the functions
7644:{\displaystyle S\subset \mathbb {C} }
6174:that allows it to reach or dip below
4580:{\displaystyle (f_{\alpha }(x),f(x))}
3645:Intuitively, a sequence of functions
781:is larger than or equal to a certain
253:{\displaystyle f_{n}(x)=\sin ^{n}(x)}
12121:If the domain of the functions is a
11285:which uniformly converge with limit
10441:by taking the limit of the sequence
9233:, then (uniform) convergence of the
7815:{\displaystyle |f_{n}(x)|\leq M_{n}}
1764:
562:. Described in an informal way, if
12945:1 − 1 + 1 − 1 + ⋯ (Grandi's series)
12544:Principles of Mathematical Analysis
12470:Principles of Mathematical Analysis
12326:Almost uniform convergence implies
11196:
9495:to produce the desired inequality.
2486:without an adverb is taken to mean
1941:{\displaystyle f:E\to \mathbb {R} }
1514:, and, with additional hypotheses,
1160:could depend on the values of both
13:
12344:Uniform convergence in probability
12062:
11944:
11818:
11775:
11607:
11387:
11246:
11116:
11026:converges uniformly to a function
10845:
10006:
9895:
9776:It follows from the continuity of
9637:
9491:), and then combines them via the
9049:sequence that converges pointwise.
8638:
8557:
8508:
8455:
8223:
8016:
7586:
7532:
7446:
7388:
7359:
7338:. In fact, it is easy to see that
6329:. Moreover, for a fixed choice of
5648:
5579:
5336:
5307:
5201:
4234:
3799:all fall within a "tube" of width
3065:
2600:
2416:
2413:
2410:
2407:
2404:
2401:
2398:
2395:
2392:
2333:
2310:
2287:
2284:
2281:
2278:
2236:
2225:
2222:
2219:
2213:
2210:
2207:
2204:
1703:) which he used in his 1841 paper
1595:
14:
13153:
13063:Generalized hypergeometric series
12571:
12285:
11558:
11433:sufficiently large, the graph of
10247:which gives us the continuity of
9601:{\displaystyle \varepsilon >0}
8968:functions with a pointwise limit
8140:on the terms of the series, with
7415:contrary to the requirement that
6990:{\displaystyle x_{0}=(1/2)^{1/N}}
6693:{\displaystyle f_{n}(x_{0})=1/2.}
4595:Definition in a hyperreal setting
3739:{\displaystyle N\in \mathbb {N} }
761:, we only need to make sure that
13101:
13100:
13073:Lauricella hypergeometric series
12791:
10886:exists (and is finite) for some
9058:
7253:{\displaystyle f_{n}\ (n\geq N)}
4874:does not. Specifically, assume
4373:{\displaystyle d(f_{n}(x),f(x))}
4124:{\displaystyle N=N(\epsilon ,x)}
3219:{\displaystyle \mathbb {R} ^{E}}
2740:, there exists a natural number
2580:{\displaystyle f_{n}(x)\to f(x)}
1641:is independent of the variables
1358:may require a different, larger
1133:{\displaystyle N=N(\epsilon ,x)}
13083:Riemann's differential equation
12602:from the University of Colorado
12099:and the series of integrals of
11521:{\displaystyle \varepsilon |I|}
10301:
10018:
9907:
9649:
9479:This theorem is proved by the "
9053:
7885:{\displaystyle n=1,2,3,\ldots }
5918:{\displaystyle f_{n}(1)=f(1)=1}
5861:{\displaystyle f_{n}(0)=f(0)=0}
4634:uniformly if for all hyperreal
4313:{\displaystyle |f_{n}(x)-f(x)|}
3692:if, given an arbitrarily small
2390:
2302:
2261:
2200:
1970:{\displaystyle \epsilon >0,}
1073:merely guarantees that for any
741:by less than a chosen distance
12461:
12427:
12413:. AMS Bookstore. p. 184.
12398:
12371:
12262:
12249:
12195:there exists a measurable set
12165:converges almost uniformly on
12152:
12139:
12013:
12001:
11839:
11824:
11772:
11707:
11701:
11664:
11658:
11514:
11506:
11384:
11231:
11217:
11178:
11166:
11140:
11134:
11113:
11099:
11093:
11065:
11053:
10986:
10974:
10954:
10938:
10918:
10906:
10873:
10860:
10842:
10814:
10802:
10782:
10769:
10649:
10643:
10576:
10545:
10536:
10502:
10496:
10308:{\displaystyle \quad \square }
10225:
10222:
10209:
10200:
10187:
10174:
10165:
10162:
10149:
10133:
10127:
10114:
10105:
10102:
10096:
10080:
10074:
10068:
10059:
10056:
10043:
10034:
10028:
10022:
9962:
9959:
9946:
9930:
9924:
9911:
9690:
9687:
9681:
9672:
9666:
9653:
9419:
9386:
9350:
9337:
9202:{\displaystyle f_{n},f:E\to M}
9193:
9099:
9093:
9032:
9019:
8943:
8937:
8915:
8909:
8875:
8862:
8769:{\displaystyle S\subset D_{R}}
8635:
8615:
8603:
8554:
8505:
8314:
8305:
8109:centered on the origin in the
7795:
7791:
7785:
7771:
7718:
7682:
7669:
7583:
7555:
7552:
7540:
7537:
7484:
7451:
7356:
7325:
7313:
7247:
7235:
7202:
7190:
7057:
7044:
7035:
7022:
6970:
6955:
6849:
6837:
6804:
6800:
6794:
6785:
6779:
6765:
6730:{\displaystyle \epsilon =1/4,}
6673:
6660:
6636:{\displaystyle x_{0}\in [0,1)}
6630:
6618:
6555:
6551:
6545:
6536:
6530:
6516:
6469:
6457:
6414:{\displaystyle \epsilon >0}
6393:Non-uniformity of convergence:
6256:
6244:
6215:
6056:
6052:
6046:
6037:
6031:
6017:
6002:{\displaystyle \epsilon >0}
5970:
5958:
5906:
5900:
5891:
5885:
5849:
5843:
5834:
5828:
5709:
5697:
5669:
5663:
5645:
5631:
5625:
5576:
5553:
5540:
5477:
5471:
5454:
5442:
5439:
5436:
5424:
5381:
5368:
5304:
5258:
5254:
5248:
5239:
5233:
5226:
5178:
5166:
5056:is only less than or equal to
4930:
4915:
4822:
4807:
4787:
4775:
4733:
4727:
4697:
4691:
4574:
4571:
4565:
4556:
4550:
4537:
4423:
4410:
4367:
4364:
4358:
4349:
4343:
4330:
4306:
4302:
4296:
4287:
4281:
4267:
4118:
4106:
3997:{\displaystyle N=N(\epsilon )}
3991:
3985:
3905:{\displaystyle f(x)+\epsilon }
3893:
3887:
3870:{\displaystyle f(x)-\epsilon }
3858:
3852:
3711:{\displaystyle \epsilon >0}
3615:
3603:
3580:
3567:
3433:
3419:
3392:
3389:
3370:
3363:
3356:
3316:
3312:
3306:
3297:
3291:
3284:
3261:
3249:
3167:
3153:
3099:
3085:
3062:
3036:
2952:
2948:
2942:
2933:
2927:
2913:
2849:
2845:
2839:
2823:
2817:
2803:
2798:
2733:{\displaystyle \epsilon >0}
2667:
2653:
2597:
2574:
2568:
2562:
2559:
2553:
2450:
2384:
2330:
2274:
2233:
2191:
2098:
2094:
2088:
2079:
2073:
2059:
1977:there exists a natural number
1930:
1863:
1849:
1815:
1801:
1628:
1610:
1451:
1447:
1441:
1432:
1426:
1412:
1299:
1293:
1250:
1244:
1127:
1115:
1099:given in advance, we can find
978:
974:
968:
959:
953:
939:
855:{\displaystyle N=N(\epsilon )}
849:
843:
728:
722:
699:
693:
311:
298:
247:
241:
222:
216:
43:
30:
1:
13078:Modular hypergeometric series
12919:1/4 + 1/16 + 1/64 + 1/256 + ⋯
12546:, 3rd ed., McGraw–Hill, 1976.
12480:
12328:almost everywhere convergence
9209:. If we further assume that
8801:
7659:Theorem (Weierstrass M-test).
5084:at ever increasing values of
5009:, regardless of the value of
4901:{\displaystyle \epsilon =1/4}
4429:{\displaystyle (f_{\alpha })}
3965:" results in a definition of
3630:{\displaystyle B(x,r)\cap E.}
1746:
12188:{\displaystyle \delta >0}
11781:{\displaystyle n\to \infty }
11579:
9395:{\displaystyle f_{n}:E\to M}
9105:{\displaystyle \sin ^{n}(x)}
8680:which means the series over
7619:The series expansion of the
6598:becomes, there is always an
5585:{\displaystyle n\to \infty }
5134:, we can equip the space of
4703:{\displaystyle f_{n}^{*}(x)}
3462:locally uniformly convergent
3071:{\displaystyle n\to \infty }
2631:{\displaystyle \mathbb {R} }
2606:{\displaystyle n\to \infty }
1705:Zur Theorie der Potenzreihen
7:
13137:Topology of function spaces
13088:Theta hypergeometric series
12587:Encyclopedia of Mathematics
12565:An Introduction to Analysis
12405:Jahnke, Hans Niels (2003).
12337:
12215:{\displaystyle E_{\delta }}
12128:then the related notion of
8736:{\displaystyle z\in D_{R},}
7959:{\textstyle \sum _{n}f_{n}}
7922:{\textstyle \sum _{n}M_{n}}
7695:be a sequence of functions
5759:Convergence is trivial for
4948:{\displaystyle (1/2)^{x+n}}
4847:converges uniformly, while
4840:{\displaystyle (1/2)^{x+n}}
4757:
4482:{\displaystyle \alpha _{0}}
3146:as (simple) convergence of
280:of functions stronger than
10:
13158:
12970:Infinite arithmetic series
12914:1/2 + 1/4 + 1/8 + 1/16 + ⋯
12909:1/2 − 1/4 + 1/8 − 1/16 + ⋯
12364:
12130:almost uniform convergence
12117:Almost uniform convergence
9829:{\displaystyle x_{0}\in E}
9528:{\displaystyle x_{0}\in E}
9062:
9012:is a compact interval and
6269:. Note that the choice of
6224:{\displaystyle f_{n}\to f}
5976:{\displaystyle x\in (0,1)}
5361:The sequence of functions
4793:{\displaystyle x\in [0,1)}
4603:setting. Thus, a sequence
4070:, for a specific value of
3815:{\displaystyle 2\epsilon }
3045:{\displaystyle d_{n}\to 0}
2459:{\displaystyle f_{n}\to f}
1544:
13142:Convergence (mathematics)
13096:
13053:
12997:
12932:
12901:
12894:
12864:
12833:
12826:
12800:
12789:
12712:
12656:
12647:
12519:, pp. 148–156 (1918)
10924:{\displaystyle x_{0}\in }
9310:is a topological space,
7273:{\displaystyle \epsilon }
6342:{\displaystyle \epsilon }
6302:{\displaystyle \epsilon }
6187:{\displaystyle \epsilon }
4955:is less than or equal to
4451:if and only if for every
4204:{\displaystyle \epsilon }
4144:{\displaystyle \epsilon }
4083:{\displaystyle \epsilon }
4017:{\displaystyle \epsilon }
3019:uniformly if and only if
1709:Philipp Ludwig von Seidel
1518:, are transferred to the
1276:{\displaystyle \epsilon }
1173:{\displaystyle \epsilon }
875:{\displaystyle \epsilon }
754:{\displaystyle \epsilon }
511:{\displaystyle \epsilon }
380:{\displaystyle \epsilon }
156:{\displaystyle \epsilon }
89:{\displaystyle \epsilon }
76:when for arbitrary small
12567:, 3rd ed., Pearson, 2005
12392:10.1016/j.hm.2004.11.010
11895:be contained in the set
10960:{\displaystyle (f'_{n})}
10396:and converge to a limit
7611:is not even continuous.
6908:, consider the value of
6444:there will be values of
6289:depends on the value of
4739:{\displaystyle f^{*}(x)}
3640:
1687:Later Gudermann's pupil
1256:{\displaystyle f_{n}(x)}
705:{\displaystyle f_{n}(x)}
656:is "uniform" throughout
185:{\displaystyle n\geq N.}
163:-tube around f whenever
23:A sequence of functions
12801:Properties of sequences
12275:converges uniformly on
12268:{\displaystyle (f_{n})}
12235:{\displaystyle \delta }
12222:with measure less than
12158:{\displaystyle (f_{n})}
12087:converges uniformly on
11969:converges uniformly on
11762:converges uniformly as
10967:converges uniformly on
10788:{\displaystyle (f_{n})}
9739:{\displaystyle n\geq N}
9356:{\displaystyle (f_{n})}
9330:is a metric space, and
9038:{\displaystyle (f_{n})}
8881:{\displaystyle (f_{n})}
7688:{\displaystyle (f_{n})}
6881:{\displaystyle n\geq N}
6501:{\displaystyle n\geq N}
6095:{\displaystyle n\geq N}
5559:{\displaystyle (f_{n})}
5387:{\displaystyle (f_{n})}
5145:-valued functions over
5002:{\displaystyle n\geq 2}
4710:is infinitely close to
3672:converges uniformly to
3593:converges uniformly on
3586:{\displaystyle (f_{n})}
2694:converges uniformly on
2016:{\displaystyle n\geq N}
1397:{\displaystyle n\geq N}
1331:{\displaystyle n\geq N}
924:{\displaystyle n\geq N}
327:to a limiting function
317:{\displaystyle (f_{n})}
116:such that the graph of
56:converges uniformly to
49:{\displaystyle (f_{n})}
12664:Arithmetic progression
12467:Rudin, Walter (1976).
12440:Proofs and Refutations
12332:convergence in measure
12302:
12269:
12236:
12216:
12189:
12159:
12114:
12081:
12066:
12020:
11963:
11948:
11873:
11872:{\displaystyle x\in E}
11847:
11822:
11782:
11740:
11739:{\displaystyle x\in E}
11714:
11690:
11626:
11611:
11542:
11522:
11489:
11454:
11419:
11346:
11319:
11299:
11279:
11255:
11185:
11147:
11072:
11040:
11020:
10993:
10961:
10925:
10880:
10821:
10789:
10750:
10722:
10721:{\displaystyle f'_{n}}
10692:
10617:
10592:
10553:
10465:
10464:{\displaystyle f'_{n}}
10435:
10410:
10386:
10359:
10309:
10288:
10261:
10238:
9984:
9880:
9853:
9830:
9797:
9767:
9740:
9712:
9622:
9602:
9576:
9549:
9529:
9469:
9449:
9429:
9396:
9357:
9324:
9304:
9274:
9254:
9223:
9203:
9150:
9130:
9113:
9106:
9039:
9006:
8982:
8950:
8882:
8845:
8819:locally compact spaces
8793:
8770:
8737:
8701:
8671:
8474:
8459:
8424:
8364:
8258:To do this, we notice
8249:
8161:
8134:
8103:
8080:
8050:
8020:
7980:
7960:
7923:
7886:
7842:
7841:{\displaystyle x\in E}
7816:
7757:
7730:
7689:
7645:
7605:
7562:
7494:
7461:
7406:
7332:
7294:
7274:
7254:
7209:
7168:
6991:
6929:
6902:
6882:
6856:
6818:
6751:
6731:
6694:
6637:
6592:
6572:
6502:
6476:
6438:
6415:
6383:
6363:
6343:
6323:
6303:
6283:
6263:
6225:
6188:
6168:
6148:
6096:
6070:
6003:
5977:
5939:
5919:
5862:
5805:
5779:
5757:Pointwise convergence:
5747:
5606:
5586:
5560:
5527:
5504:
5388:
5351:
5269:
5118:
5098:
5078:
5050:
5023:
5003:
4977:
4949:
4902:
4868:
4841:
4794:
4740:
4704:
4659:
4624:
4581:
4524:
4489:, such that for every
4483:
4430:
4403:. We say that the net
4374:
4314:
4225:
4205:
4185:
4165:
4145:
4125:
4084:
4064:
4063:{\displaystyle x\in E}
4038:
4018:
3998:
3959:
3939:
3938:{\displaystyle x\in E}
3906:
3871:
3836:
3816:
3793:
3792:{\displaystyle n>N}
3767:
3746:so that the functions
3740:
3712:
3686:
3666:
3631:
3587:
3554:
3553:{\displaystyle r>0}
3528:
3527:{\displaystyle x\in E}
3498:
3478:
3454:
3402:
3327:
3220:
3188:
3140:
3120:
3072:
3046:
3013:
2993:
2963:
2863:
2754:
2734:
2708:
2688:
2632:
2607:
2581:
2530:
2529:{\displaystyle x\in E}
2504:
2480:
2460:
2424:
2355:
2165:
2145:
2115:
2043:
2042:{\displaystyle x\in E}
2017:
1991:
1971:
1942:
1908:
1884:
1836:
1784:
1700:
1693:gleichmäßig konvergent
1678:
1677:{\displaystyle \psi .}
1655:
1635:
1599:
1568:, in an 1838 paper on
1535:
1500:
1465:
1398:
1372:
1352:
1332:
1306:
1277:
1257:
1220:
1195:
1174:
1154:
1134:
1093:
1092:{\displaystyle x\in E}
1067:
1047:
1019:
1018:{\displaystyle x\in E}
992:
925:
898:
876:
856:
821:
820:{\displaystyle x\in E}
795:
775:
755:
735:
706:
670:
650:
630:
603:
583:
556:
534:
512:
492:
472:
401:
381:
361:
341:
318:
261:
254:
192:
186:
157:
137:
110:
90:
70:
50:
13055:Hypergeometric series
12669:Geometric progression
12582:"Uniform convergence"
12411:A history of analysis
12359:Arzelà–Ascoli theorem
12303:
12270:
12237:
12217:
12190:
12160:
12082:
12046:
12021:
11964:
11928:
11886:
11874:
11848:
11802:
11783:
11741:
11715:
11670:
11627:
11591:
11543:
11523:
11490:
11488:{\displaystyle f_{n}}
11455:
11453:{\displaystyle f_{n}}
11420:
11347:
11345:{\displaystyle f_{n}}
11320:
11300:
11280:
11256:
11186:
11184:{\displaystyle x\in }
11148:
11073:
11041:
11021:
11019:{\displaystyle f_{n}}
10994:
10962:
10926:
10881:
10822:
10790:
10751:
10728:does not converge to
10723:
10693:
10618:
10593:
10554:
10466:
10436:
10411:
10387:
10385:{\displaystyle f_{n}}
10360:
10310:
10289:
10287:{\displaystyle x_{0}}
10262:
10239:
9985:
9881:
9879:{\displaystyle x_{0}}
9854:
9836:that there exists an
9831:
9798:
9796:{\displaystyle f_{N}}
9768:
9766:{\displaystyle f_{N}}
9741:
9713:
9623:
9603:
9577:
9575:{\displaystyle x_{0}}
9550:
9530:
9470:
9450:
9430:
9397:
9358:
9325:
9305:
9285:Uniform limit theorem
9275:
9255:
9253:{\displaystyle f_{n}}
9224:
9204:
9151:
9131:
9107:
9072:
9065:Uniform limit theorem
9040:
9007:
8983:
8951:
8883:
8846:
8794:
8771:
8738:
8702:
8700:{\displaystyle M_{n}}
8672:
8475:
8439:
8425:
8365:
8250:
8162:
8160:{\displaystyle M_{n}}
8135:
8133:{\displaystyle M_{n}}
8104:
8081:
8079:{\displaystyle D_{R}}
8051:
8000:
7981:
7961:
7924:
7887:
7843:
7817:
7758:
7756:{\displaystyle M_{n}}
7731:
7690:
7646:
7606:
7563:
7495:
7462:
7407:
7333:
7331:{\displaystyle x\in }
7295:
7275:
7255:
7210:
7208:{\displaystyle x\in }
7169:
6992:
6930:
6928:{\displaystyle f_{N}}
6903:
6883:
6857:
6855:{\displaystyle x\in }
6819:
6752:
6737:we can never find an
6732:
6695:
6638:
6593:
6573:
6503:
6477:
6475:{\displaystyle x\in }
6439:
6416:
6384:
6364:
6344:
6324:
6304:
6284:
6264:
6262:{\displaystyle x\in }
6226:
6189:
6169:
6149:
6097:
6071:
6009:, we can ensure that
6004:
5978:
5940:
5920:
5863:
5806:
5780:
5748:
5607:
5587:
5561:
5528:
5505:
5389:
5352:
5270:
5119:
5099:
5079:
5051:
5049:{\displaystyle x^{n}}
5029:. On the other hand,
5024:
5004:
4978:
4950:
4903:
4869:
4867:{\displaystyle x^{n}}
4842:
4795:
4741:
4705:
4660:
4658:{\displaystyle f^{*}}
4625:
4623:{\displaystyle f_{n}}
4582:
4525:
4484:
4431:
4375:
4315:
4226:
4206:
4186:
4166:
4146:
4126:
4085:
4065:
4039:
4019:
3999:
3967:pointwise convergence
3960:
3940:
3907:
3872:
3837:
3817:
3794:
3768:
3766:{\displaystyle f_{n}}
3741:
3713:
3687:
3667:
3665:{\displaystyle f_{n}}
3632:
3588:
3555:
3529:
3499:
3479:
3455:
3403:
3328:
3236:metric), defined by
3221:
3189:
3141:
3121:
3073:
3047:
3014:
2994:
2992:{\displaystyle f_{n}}
2964:
2864:
2755:
2735:
2709:
2689:
2640:complete metric space
2633:
2608:
2582:
2531:
2505:
2488:pointwise convergence
2481:
2461:
2425:
2356:
2166:
2146:
2144:{\displaystyle f_{n}}
2116:
2044:
2018:
1992:
1972:
1943:
1909:
1885:
1837:
1785:
1759:and, more generally,
1753:real-valued functions
1713:George Gabriel Stokes
1679:
1656:
1654:{\displaystyle \phi }
1636:
1579:
1551:Augustin-Louis Cauchy
1536:
1512:Riemann integrability
1501:
1499:{\displaystyle f_{n}}
1466:
1399:
1373:
1353:
1333:
1307:
1278:
1258:
1221:
1196:
1175:
1155:
1135:
1094:
1068:
1048:
1046:{\displaystyle f_{n}}
1020:
993:
926:
905:, such that choosing
899:
877:
862:that could depend on
857:
822:
796:
776:
756:
736:
707:
671:
651:
631:
629:{\displaystyle f_{n}}
604:
584:
582:{\displaystyle f_{n}}
557:
535:
513:
493:
473:
402:
382:
362:
342:
319:
282:pointwise convergence
255:
198:
187:
158:
138:
136:{\displaystyle f_{n}}
111:
91:
71:
51:
22:
13035:Trigonometric series
12827:Properties of series
12674:Harmonic progression
12380:Historia Mathematica
12279:
12246:
12226:
12199:
12173:
12136:
12043:
11992:
11919:
11857:
11853:converges for every
11799:
11766:
11724:
11720:converges for every
11645:
11588:
11574:Weierstrass function
11532:
11499:
11472:
11437:
11357:
11329:
11309:
11289:
11269:
11214:
11157:
11082:
11050:
11030:
11003:
10971:
10935:
10890:
10831:
10799:
10766:
10732:
10702:
10627:
10602:
10563:
10483:
10477:Weierstrass function
10445:
10420:
10400:
10369:
10349:
10341:To differentiability
10330:uniformly continuous
10298:
10271:
10251:
10003:
9892:
9863:
9843:
9807:
9780:
9750:
9724:
9634:
9612:
9586:
9559:
9539:
9506:
9475:is also continuous.
9459:
9439:
9406:
9367:
9334:
9314:
9294:
9264:
9237:
9213:
9168:
9140:
9120:
9077:
9016:
8996:
8972:
8896:
8859:
8835:
8812:compactly convergent
8780:
8747:
8711:
8684:
8494:
8436:
8377:
8265:
8174:
8144:
8117:
8090:
8063:
7997:
7970:
7933:
7896:
7852:
7826:
7767:
7740:
7699:
7666:
7627:
7621:exponential function
7615:Exponential function
7572:
7511:
7471:
7419:
7345:
7304:
7284:
7264:
7219:
7181:
7004:
6939:
6912:
6892:
6866:
6828:
6761:
6741:
6704:
6647:
6602:
6582:
6512:
6486:
6448:
6425:
6399:
6373:
6353:
6333:
6313:
6293:
6273:
6235:
6202:
6178:
6158:
6106:
6080:
6013:
5987:
5949:
5929:
5872:
5815:
5789:
5763:
5619:
5596:
5570:
5537:
5517:
5400:
5365:
5293:
5160:
5108:
5088:
5060:
5033:
5013:
4987:
4959:
4912:
4878:
4851:
4804:
4766:
4714:
4673:
4642:
4607:
4534:
4501:
4466:
4407:
4324:
4263:
4215:
4195:
4175:
4171:, and the choice of
4155:
4135:
4094:
4074:
4048:
4044:has to work for all
4028:
4024:, and the choice of
4008:
3973:
3949:
3923:
3881:
3846:
3826:
3803:
3777:
3750:
3722:
3696:
3676:
3649:
3597:
3564:
3538:
3512:
3488:
3468:
3416:
3343:
3243:
3226:with respect to the
3201:
3150:
3130:
3082:
3056:
3023:
3003:
2976:
2880:
2767:
2744:
2718:
2698:
2650:
2620:
2591:
2540:
2514:
2494:
2470:
2437:
2371:
2178:
2155:
2128:
2055:
2027:
2001:
1981:
1952:
1918:
1898:
1892:uniformly convergent
1846:
1798:
1774:
1733:Paul du Bois-Reymond
1701:uniformly convergent
1665:
1645:
1576:
1525:
1483:
1408:
1382:
1362:
1342:
1316:
1305:{\displaystyle f(x)}
1287:
1267:
1231:
1210:
1185:
1164:
1144:
1103:
1077:
1057:
1030:
1003:
935:
909:
888:
866:
831:
805:
785:
765:
745:
734:{\displaystyle f(x)}
716:
680:
660:
640:
613:
593:
566:
546:
524:
502:
482:
411:
391:
371:
351:
331:
295:
203:
167:
147:
120:
100:
80:
60:
27:
13132:Mathematical series
13015:Formal power series
11250:
11133:
10953:
10749:{\displaystyle f',}
10717:
10642:
10559:with uniform limit
10460:
9995:triangle inequality
9493:triangle inequality
9288: —
8890:monotone increasing
6700:Thus, if we choose
5804:{\displaystyle x=1}
5778:{\displaystyle x=0}
5077:{\displaystyle 1/4}
4976:{\displaystyle 1/4}
4690:
4437:converges uniformly
4131:may depend on both
4004:can only depend on
1566:Christoph Gudermann
1204:for that particular
325:converges uniformly
278:mode of convergence
274:uniform convergence
12813:Monotonic function
12732:Fibonacci sequence
12298:
12265:
12232:
12212:
12185:
12155:
12077:
12019:{\displaystyle E=}
12016:
11959:
11869:
11843:
11778:
11736:
11710:
11622:
11538:
11518:
11485:
11450:
11415:
11391:
11342:
11315:
11295:
11275:
11251:
11230:
11181:
11143:
11121:
11120:
11068:
11036:
11016:
10989:
10957:
10941:
10921:
10876:
10849:
10817:
10785:
10746:
10718:
10705:
10688:
10630:
10616:{\displaystyle f'}
10613:
10588:
10549:
10461:
10448:
10434:{\displaystyle f'}
10431:
10406:
10382:
10355:
10305:
10284:
10257:
10234:
9980:
9978:
9876:
9849:
9826:
9793:
9763:
9736:
9708:
9706:
9618:
9598:
9572:
9545:
9525:
9500:
9465:
9445:
9425:
9392:
9353:
9320:
9300:
9286:
9270:
9250:
9219:
9199:
9158:topological spaces
9146:
9126:
9114:
9102:
9035:
9002:
8978:
8946:
8892:sequence (meaning
8878:
8841:
8792:{\displaystyle S.}
8789:
8766:
8733:
8697:
8667:
8642:
8561:
8512:
8487:can be used here:
8470:
8420:
8415:
8360:
8245:
8157:
8130:
8102:{\displaystyle R,}
8099:
8076:
8046:
7976:
7956:
7945:
7919:
7908:
7882:
7838:
7812:
7753:
7726:
7685:
7653:Weierstrass M-test
7641:
7601:
7590:
7558:
7490:
7457:
7402:
7363:
7328:
7290:
7270:
7250:
7205:
7164:
6987:
6925:
6898:
6878:
6852:
6814:
6747:
6727:
6690:
6633:
6588:
6568:
6498:
6472:
6437:{\displaystyle N,}
6434:
6411:
6379:
6359:
6339:
6319:
6299:
6279:
6259:
6231:pointwise for all
6221:
6184:
6164:
6144:
6092:
6066:
5999:
5973:
5935:
5915:
5858:
5801:
5775:
5743:
5738:
5652:
5602:
5582:
5556:
5523:
5500:
5495:
5384:
5347:
5311:
5265:
5224:
5114:
5094:
5074:
5046:
5019:
4999:
4973:
4945:
4898:
4864:
4837:
4790:
4736:
4700:
4676:
4655:
4620:
4577:
4520:
4479:
4462:, there exists an
4426:
4370:
4310:
4221:
4201:
4181:
4161:
4141:
4121:
4080:
4060:
4034:
4014:
3994:
3955:
3935:
3902:
3867:
3832:
3812:
3789:
3763:
3736:
3708:
3682:
3662:
3627:
3583:
3550:
3534:, there exists an
3524:
3494:
3474:
3450:
3398:
3323:
3282:
3216:
3184:
3136:
3116:
3068:
3042:
3009:
2989:
2959:
2911:
2859:
2750:
2730:
2704:
2684:
2628:
2603:
2577:
2526:
2500:
2476:
2456:
2420:
2351:
2337:
2240:
2161:
2141:
2111:
2039:
2013:
1997:such that for all
1987:
1967:
1938:
1904:
1880:
1832:
1780:
1674:
1651:
1631:
1570:elliptic functions
1531:
1496:
1461:
1404:to guarantee that
1394:
1368:
1348:
1328:
1302:
1273:
1253:
1216:
1191:
1170:
1150:
1130:
1089:
1063:
1043:
1015:
988:
921:
894:
872:
852:
817:
791:
771:
751:
731:
702:
666:
646:
626:
599:
579:
552:
530:
508:
488:
468:
397:
377:
357:
337:
314:
262:
250:
193:
182:
153:
133:
106:
96:there is an index
86:
66:
46:
13114:
13113:
13045:Generating series
12993:
12992:
12965:1 − 2 + 4 − 8 + ⋯
12960:1 + 2 + 4 + 8 + ⋯
12955:1 − 2 + 3 − 4 + ⋯
12950:1 + 2 + 3 + 4 + ⋯
12940:1 + 1 + 1 + 1 + ⋯
12890:
12889:
12818:Periodic sequence
12787:
12786:
12772:Triangular number
12762:Pentagonal number
12742:Heptagonal number
12727:Complete sequence
12649:Integer sequences
12454:978-0-521-21078-2
12420:978-0-8218-2623-2
12321:almost everywhere
12313:almost everywhere
12095:is integrable on
12035:is integrable on
11977:is continuous at
11908:be continuous at
11553:Lebesgue integral
11541:{\displaystyle f}
11376:
11318:{\displaystyle f}
11298:{\displaystyle f}
11278:{\displaystyle I}
11105:
11039:{\displaystyle f}
10931:and the sequence
10834:
10698:and the sequence
10409:{\displaystyle f}
10358:{\displaystyle S}
10260:{\displaystyle f}
9993:Hence, using the
9977:
9852:{\displaystyle U}
9705:
9621:{\displaystyle N}
9555:is continuous at
9548:{\displaystyle f}
9498:
9468:{\displaystyle f}
9448:{\displaystyle E}
9323:{\displaystyle M}
9303:{\displaystyle E}
9284:
9273:{\displaystyle f}
9222:{\displaystyle M}
9164:of the functions
9149:{\displaystyle M}
9129:{\displaystyle E}
9005:{\displaystyle S}
8981:{\displaystyle f}
8844:{\displaystyle S}
8659:
8627:
8622:
8590:
8546:
8541:
8497:
8414:
8358:
8333:
8292:
8201:
8041:
7979:{\displaystyle E}
7936:
7899:
7575:
7348:
7293:{\displaystyle f}
7234:
7153:
7140:
7105:
7091:
6901:{\displaystyle N}
6750:{\displaystyle N}
6591:{\displaystyle n}
6382:{\displaystyle x}
6362:{\displaystyle N}
6322:{\displaystyle x}
6282:{\displaystyle N}
6167:{\displaystyle x}
5938:{\displaystyle n}
5637:
5605:{\displaystyle f}
5526:{\displaystyle f}
5296:
5209:
5129:topological space
5117:{\displaystyle x}
5097:{\displaystyle n}
5022:{\displaystyle x}
4665:and all infinite
4638:in the domain of
4224:{\displaystyle x}
4184:{\displaystyle N}
4164:{\displaystyle x}
4037:{\displaystyle N}
3958:{\displaystyle N}
3916:of the function.
3835:{\displaystyle f}
3718:, we can find an
3685:{\displaystyle f}
3497:{\displaystyle E}
3477:{\displaystyle f}
3267:
3232:(also called the
3139:{\displaystyle E}
3012:{\displaystyle f}
2896:
2753:{\displaystyle N}
2707:{\displaystyle E}
2503:{\displaystyle E}
2479:{\displaystyle E}
2322:
2294:
2218:
2202:
2164:{\displaystyle f}
1990:{\displaystyle N}
1907:{\displaystyle E}
1783:{\displaystyle E}
1555:Niels Henrik Abel
1534:{\displaystyle f}
1516:differentiability
1371:{\displaystyle N}
1351:{\displaystyle x}
1338:(and a different
1219:{\displaystyle x}
1194:{\displaystyle x}
1153:{\displaystyle N}
1066:{\displaystyle f}
931:will ensure that
897:{\displaystyle x}
794:{\displaystyle N}
774:{\displaystyle n}
669:{\displaystyle E}
649:{\displaystyle f}
602:{\displaystyle f}
555:{\displaystyle E}
533:{\displaystyle x}
491:{\displaystyle f}
400:{\displaystyle N}
360:{\displaystyle E}
340:{\displaystyle f}
109:{\displaystyle N}
69:{\displaystyle f}
13149:
13104:
13103:
13030:Dirichlet series
12899:
12898:
12831:
12830:
12795:
12767:Polygonal number
12747:Hexagonal number
12720:
12654:
12653:
12630:
12623:
12616:
12607:
12606:
12595:
12566:
12545:
12528:
12510:
12492:
12474:
12465:
12459:
12458:
12431:
12425:
12424:
12402:
12396:
12395:
12375:
12317:Egorov's theorem
12307:
12305:
12304:
12299:
12297:
12296:
12274:
12272:
12271:
12266:
12261:
12260:
12241:
12239:
12238:
12233:
12221:
12219:
12218:
12213:
12211:
12210:
12194:
12192:
12191:
12186:
12164:
12162:
12161:
12156:
12151:
12150:
12086:
12084:
12083:
12078:
12076:
12075:
12065:
12060:
12025:
12023:
12022:
12017:
11968:
11966:
11965:
11960:
11958:
11957:
11947:
11942:
11878:
11876:
11875:
11870:
11852:
11850:
11849:
11844:
11842:
11837:
11836:
11827:
11821:
11816:
11787:
11785:
11784:
11779:
11745:
11743:
11742:
11737:
11719:
11717:
11716:
11711:
11700:
11699:
11689:
11684:
11657:
11656:
11631:
11629:
11628:
11623:
11621:
11620:
11610:
11605:
11565:Morera's Theorem
11548:, respectively.
11547:
11545:
11544:
11539:
11527:
11525:
11524:
11519:
11517:
11509:
11495:are each within
11494:
11492:
11491:
11486:
11484:
11483:
11464:of the graph of
11463:
11459:
11457:
11456:
11451:
11449:
11448:
11424:
11422:
11421:
11416:
11411:
11410:
11401:
11400:
11390:
11369:
11368:
11351:
11349:
11348:
11343:
11341:
11340:
11324:
11322:
11321:
11316:
11304:
11302:
11301:
11296:
11284:
11282:
11281:
11276:
11260:
11258:
11257:
11252:
11249:
11244:
11229:
11228:
11203:Riemann integral
11197:To integrability
11190:
11188:
11187:
11182:
11152:
11150:
11149:
11144:
11129:
11119:
11092:
11077:
11075:
11074:
11071:{\displaystyle }
11069:
11045:
11043:
11042:
11037:
11025:
11023:
11022:
11017:
11015:
11014:
10998:
10996:
10995:
10992:{\displaystyle }
10990:
10966:
10964:
10963:
10958:
10949:
10930:
10928:
10927:
10922:
10902:
10901:
10885:
10883:
10882:
10877:
10872:
10871:
10859:
10858:
10848:
10826:
10824:
10823:
10820:{\displaystyle }
10818:
10794:
10792:
10791:
10786:
10781:
10780:
10755:
10753:
10752:
10747:
10742:
10727:
10725:
10724:
10719:
10713:
10697:
10695:
10694:
10689:
10672:
10671:
10667:
10638:
10622:
10620:
10619:
10614:
10612:
10597:
10595:
10594:
10589:
10575:
10574:
10558:
10556:
10555:
10550:
10548:
10528:
10527:
10523:
10495:
10494:
10470:
10468:
10467:
10462:
10456:
10440:
10438:
10437:
10432:
10430:
10415:
10413:
10412:
10407:
10391:
10389:
10388:
10383:
10381:
10380:
10364:
10362:
10361:
10356:
10314:
10312:
10311:
10306:
10293:
10291:
10290:
10285:
10283:
10282:
10266:
10264:
10263:
10258:
10243:
10241:
10240:
10235:
10221:
10220:
10199:
10198:
10186:
10185:
10161:
10160:
10148:
10147:
10126:
10125:
10095:
10094:
10055:
10054:
9989:
9987:
9986:
9981:
9979:
9970:
9958:
9957:
9945:
9944:
9923:
9922:
9885:
9883:
9882:
9877:
9875:
9874:
9858:
9856:
9855:
9850:
9835:
9833:
9832:
9827:
9819:
9818:
9802:
9800:
9799:
9794:
9792:
9791:
9772:
9770:
9769:
9764:
9762:
9761:
9745:
9743:
9742:
9737:
9717:
9715:
9714:
9709:
9707:
9698:
9665:
9664:
9627:
9625:
9624:
9619:
9607:
9605:
9604:
9599:
9581:
9579:
9578:
9573:
9571:
9570:
9554:
9552:
9551:
9546:
9534:
9532:
9531:
9526:
9518:
9517:
9490:
9486:
9482:
9474:
9472:
9471:
9466:
9454:
9452:
9451:
9446:
9434:
9432:
9431:
9426:
9418:
9417:
9401:
9399:
9398:
9393:
9379:
9378:
9362:
9360:
9359:
9354:
9349:
9348:
9329:
9327:
9326:
9321:
9309:
9307:
9306:
9301:
9289:
9279:
9277:
9276:
9271:
9259:
9257:
9256:
9251:
9249:
9248:
9228:
9226:
9225:
9220:
9208:
9206:
9205:
9200:
9180:
9179:
9155:
9153:
9152:
9147:
9135:
9133:
9132:
9127:
9111:
9109:
9108:
9103:
9089:
9088:
9044:
9042:
9041:
9036:
9031:
9030:
9011:
9009:
9008:
9003:
8987:
8985:
8984:
8979:
8955:
8953:
8952:
8947:
8936:
8935:
8908:
8907:
8887:
8885:
8884:
8879:
8874:
8873:
8850:
8848:
8847:
8842:
8826:uniformly Cauchy
8798:
8796:
8795:
8790:
8775:
8773:
8772:
8767:
8765:
8764:
8742:
8740:
8739:
8734:
8729:
8728:
8706:
8704:
8703:
8698:
8696:
8695:
8676:
8674:
8673:
8668:
8660:
8658:
8644:
8641:
8623:
8621:
8601:
8593:
8591:
8589:
8588:
8579:
8578:
8563:
8560:
8542:
8540:
8539:
8530:
8529:
8514:
8511:
8479:
8477:
8476:
8471:
8469:
8468:
8458:
8453:
8429:
8427:
8426:
8421:
8416:
8413:
8405:
8404:
8395:
8389:
8388:
8369:
8367:
8366:
8361:
8359:
8357:
8349:
8348:
8339:
8334:
8332:
8324:
8323:
8322:
8317:
8308:
8302:
8297:
8293:
8291:
8283:
8282:
8273:
8254:
8252:
8251:
8246:
8241:
8240:
8219:
8218:
8206:
8202:
8200:
8192:
8191:
8182:
8166:
8164:
8163:
8158:
8156:
8155:
8139:
8137:
8136:
8131:
8129:
8128:
8108:
8106:
8105:
8100:
8085:
8083:
8082:
8077:
8075:
8074:
8055:
8053:
8052:
8047:
8042:
8040:
8032:
8031:
8022:
8019:
8014:
7985:
7983:
7982:
7977:
7965:
7963:
7962:
7957:
7955:
7954:
7944:
7929:converges, then
7928:
7926:
7925:
7920:
7918:
7917:
7907:
7891:
7889:
7888:
7883:
7847:
7845:
7844:
7839:
7821:
7819:
7818:
7813:
7811:
7810:
7798:
7784:
7783:
7774:
7762:
7760:
7759:
7754:
7752:
7751:
7735:
7733:
7732:
7727:
7725:
7711:
7710:
7694:
7692:
7691:
7686:
7681:
7680:
7650:
7648:
7647:
7642:
7640:
7610:
7608:
7607:
7602:
7600:
7599:
7589:
7567:
7565:
7564:
7559:
7536:
7535:
7523:
7522:
7499:
7497:
7496:
7491:
7483:
7482:
7466:
7464:
7463:
7458:
7450:
7449:
7434:
7433:
7411:
7409:
7408:
7403:
7392:
7391:
7376:
7375:
7362:
7337:
7335:
7334:
7329:
7299:
7297:
7296:
7291:
7279:
7277:
7276:
7271:
7259:
7257:
7256:
7251:
7232:
7231:
7230:
7214:
7212:
7211:
7206:
7173:
7171:
7170:
7165:
7154:
7146:
7141:
7133:
7128:
7124:
7117:
7116:
7111:
7107:
7106:
7098:
7096:
7092:
7084:
7064:
7060:
7056:
7055:
7034:
7033:
7021:
7020:
6996:
6994:
6993:
6988:
6986:
6985:
6981:
6965:
6951:
6950:
6934:
6932:
6931:
6926:
6924:
6923:
6907:
6905:
6904:
6899:
6887:
6885:
6884:
6879:
6861:
6859:
6858:
6853:
6823:
6821:
6820:
6815:
6807:
6778:
6777:
6768:
6756:
6754:
6753:
6748:
6736:
6734:
6733:
6728:
6720:
6699:
6697:
6696:
6691:
6686:
6672:
6671:
6659:
6658:
6642:
6640:
6639:
6634:
6614:
6613:
6597:
6595:
6594:
6589:
6577:
6575:
6574:
6569:
6558:
6529:
6528:
6519:
6507:
6505:
6504:
6499:
6481:
6479:
6478:
6473:
6443:
6441:
6440:
6435:
6420:
6418:
6417:
6412:
6388:
6386:
6385:
6380:
6368:
6366:
6365:
6360:
6348:
6346:
6345:
6340:
6328:
6326:
6325:
6320:
6308:
6306:
6305:
6300:
6288:
6286:
6285:
6280:
6268:
6266:
6265:
6260:
6230:
6228:
6227:
6222:
6214:
6213:
6196:ceiling function
6193:
6191:
6190:
6185:
6173:
6171:
6170:
6165:
6153:
6151:
6150:
6145:
6131:
6101:
6099:
6098:
6093:
6075:
6073:
6072:
6067:
6059:
6030:
6029:
6020:
6008:
6006:
6005:
6000:
5982:
5980:
5979:
5974:
5944:
5942:
5941:
5936:
5924:
5922:
5921:
5916:
5884:
5883:
5867:
5865:
5864:
5859:
5827:
5826:
5810:
5808:
5807:
5802:
5784:
5782:
5781:
5776:
5752:
5750:
5749:
5744:
5742:
5741:
5662:
5661:
5651:
5611:
5609:
5608:
5603:
5592:is the function
5591:
5589:
5588:
5583:
5565:
5563:
5562:
5557:
5552:
5551:
5532:
5530:
5529:
5524:
5509:
5507:
5506:
5501:
5499:
5498:
5492:
5491:
5470:
5469:
5420:
5419:
5393:
5391:
5390:
5385:
5380:
5379:
5356:
5354:
5353:
5348:
5340:
5339:
5324:
5323:
5310:
5274:
5272:
5271:
5266:
5261:
5229:
5223:
5205:
5204:
5123:
5121:
5120:
5115:
5103:
5101:
5100:
5095:
5083:
5081:
5080:
5075:
5070:
5055:
5053:
5052:
5047:
5045:
5044:
5028:
5026:
5025:
5020:
5008:
5006:
5005:
5000:
4982:
4980:
4979:
4974:
4969:
4954:
4952:
4951:
4946:
4944:
4943:
4925:
4908:. Each function
4907:
4905:
4904:
4899:
4894:
4873:
4871:
4870:
4865:
4863:
4862:
4846:
4844:
4843:
4838:
4836:
4835:
4817:
4799:
4797:
4796:
4791:
4745:
4743:
4742:
4737:
4726:
4725:
4709:
4707:
4706:
4701:
4689:
4684:
4664:
4662:
4661:
4656:
4654:
4653:
4629:
4627:
4626:
4621:
4619:
4618:
4586:
4584:
4583:
4578:
4549:
4548:
4529:
4527:
4526:
4521:
4519:
4518:
4488:
4486:
4485:
4480:
4478:
4477:
4435:
4433:
4432:
4427:
4422:
4421:
4379:
4377:
4376:
4371:
4342:
4341:
4319:
4317:
4316:
4311:
4309:
4280:
4279:
4270:
4230:
4228:
4227:
4222:
4210:
4208:
4207:
4202:
4190:
4188:
4187:
4182:
4170:
4168:
4167:
4162:
4150:
4148:
4147:
4142:
4130:
4128:
4127:
4122:
4089:
4087:
4086:
4081:
4069:
4067:
4066:
4061:
4043:
4041:
4040:
4035:
4023:
4021:
4020:
4015:
4003:
4001:
4000:
3995:
3964:
3962:
3961:
3956:
3944:
3942:
3941:
3936:
3911:
3909:
3908:
3903:
3876:
3874:
3873:
3868:
3841:
3839:
3838:
3833:
3822:centered around
3821:
3819:
3818:
3813:
3798:
3796:
3795:
3790:
3772:
3770:
3769:
3764:
3762:
3761:
3745:
3743:
3742:
3737:
3735:
3717:
3715:
3714:
3709:
3691:
3689:
3688:
3683:
3671:
3669:
3668:
3663:
3661:
3660:
3636:
3634:
3633:
3628:
3592:
3590:
3589:
3584:
3579:
3578:
3559:
3557:
3556:
3551:
3533:
3531:
3530:
3525:
3503:
3501:
3500:
3495:
3483:
3481:
3480:
3475:
3459:
3457:
3456:
3451:
3449:
3448:
3447:
3431:
3430:
3407:
3405:
3404:
3399:
3382:
3381:
3355:
3354:
3332:
3330:
3329:
3324:
3319:
3287:
3281:
3225:
3223:
3222:
3217:
3215:
3214:
3209:
3193:
3191:
3190:
3185:
3183:
3182:
3181:
3165:
3164:
3145:
3143:
3142:
3137:
3125:
3123:
3122:
3117:
3115:
3114:
3113:
3097:
3096:
3077:
3075:
3074:
3069:
3051:
3049:
3048:
3043:
3035:
3034:
3018:
3016:
3015:
3010:
2998:
2996:
2995:
2990:
2988:
2987:
2968:
2966:
2965:
2960:
2955:
2926:
2925:
2916:
2910:
2892:
2891:
2868:
2866:
2865:
2860:
2852:
2838:
2837:
2816:
2815:
2806:
2759:
2757:
2756:
2751:
2739:
2737:
2736:
2731:
2713:
2711:
2710:
2705:
2693:
2691:
2690:
2685:
2683:
2682:
2681:
2665:
2664:
2644:Cauchy criterion
2637:
2635:
2634:
2629:
2627:
2612:
2610:
2609:
2604:
2586:
2584:
2583:
2578:
2552:
2551:
2535:
2533:
2532:
2527:
2509:
2507:
2506:
2501:
2485:
2483:
2482:
2477:
2465:
2463:
2462:
2457:
2449:
2448:
2429:
2427:
2426:
2421:
2419:
2383:
2382:
2360:
2358:
2357:
2352:
2347:
2346:
2336:
2313:
2295:
2293:
2273:
2271:
2270:
2251:
2250:
2241:
2239:
2228:
2216:
2190:
2189:
2170:
2168:
2167:
2162:
2150:
2148:
2147:
2142:
2140:
2139:
2120:
2118:
2117:
2112:
2101:
2072:
2071:
2062:
2048:
2046:
2045:
2040:
2022:
2020:
2019:
2014:
1996:
1994:
1993:
1988:
1976:
1974:
1973:
1968:
1947:
1945:
1944:
1939:
1937:
1913:
1911:
1910:
1905:
1889:
1887:
1886:
1881:
1879:
1878:
1877:
1861:
1860:
1841:
1839:
1838:
1833:
1831:
1830:
1829:
1813:
1812:
1789:
1787:
1786:
1781:
1725:Bernhard Riemann
1689:Karl Weierstrass
1683:
1681:
1680:
1675:
1660:
1658:
1657:
1652:
1640:
1638:
1637:
1632:
1609:
1608:
1598:
1593:
1540:
1538:
1537:
1532:
1505:
1503:
1502:
1497:
1495:
1494:
1477:Karl Weierstrass
1470:
1468:
1467:
1462:
1454:
1425:
1424:
1415:
1403:
1401:
1400:
1395:
1377:
1375:
1374:
1369:
1357:
1355:
1354:
1349:
1337:
1335:
1334:
1329:
1311:
1309:
1308:
1303:
1282:
1280:
1279:
1274:
1262:
1260:
1259:
1254:
1243:
1242:
1225:
1223:
1222:
1217:
1200:
1198:
1197:
1192:
1179:
1177:
1176:
1171:
1159:
1157:
1156:
1151:
1139:
1137:
1136:
1131:
1098:
1096:
1095:
1090:
1072:
1070:
1069:
1064:
1052:
1050:
1049:
1044:
1042:
1041:
1024:
1022:
1021:
1016:
997:
995:
994:
989:
981:
952:
951:
942:
930:
928:
927:
922:
903:
901:
900:
895:
881:
879:
878:
873:
861:
859:
858:
853:
826:
824:
823:
818:
800:
798:
797:
792:
780:
778:
777:
772:
760:
758:
757:
752:
740:
738:
737:
732:
711:
709:
708:
703:
692:
691:
675:
673:
672:
667:
655:
653:
652:
647:
635:
633:
632:
627:
625:
624:
608:
606:
605:
600:
588:
586:
585:
580:
578:
577:
561:
559:
558:
553:
539:
537:
536:
531:
517:
515:
514:
509:
498:by no more than
497:
495:
494:
489:
477:
475:
474:
469:
461:
460:
442:
441:
423:
422:
406:
404:
403:
398:
386:
384:
383:
378:
366:
364:
363:
358:
346:
344:
343:
338:
323:
321:
320:
315:
310:
309:
259:
257:
256:
251:
237:
236:
215:
214:
191:
189:
188:
183:
162:
160:
159:
154:
142:
140:
139:
134:
132:
131:
115:
113:
112:
107:
95:
93:
92:
87:
75:
73:
72:
67:
55:
53:
52:
47:
42:
41:
13157:
13156:
13152:
13151:
13150:
13148:
13147:
13146:
13117:
13116:
13115:
13110:
13092:
13049:
12998:Kinds of series
12989:
12928:
12895:Explicit series
12886:
12860:
12822:
12808:Cauchy sequence
12796:
12783:
12737:Figurate number
12714:
12708:
12699:Powers of three
12643:
12634:
12580:
12574:
12564:
12543:
12526:
12508:
12490:
12483:
12478:
12477:
12466:
12462:
12455:
12432:
12428:
12421:
12403:
12399:
12376:
12372:
12367:
12340:
12292:
12288:
12280:
12277:
12276:
12256:
12252:
12247:
12244:
12243:
12227:
12224:
12223:
12206:
12202:
12200:
12197:
12196:
12174:
12171:
12170:
12146:
12142:
12137:
12134:
12133:
12119:
12111:
12107:
12071:
12067:
12061:
12050:
12044:
12041:
12040:
12034:
11993:
11990:
11989:
11988:. Suppose that
11983:
11953:
11949:
11943:
11932:
11920:
11917:
11916:
11914:
11907:
11894:
11882:
11858:
11855:
11854:
11838:
11832:
11828:
11823:
11817:
11806:
11800:
11797:
11796:
11795:if and only if
11767:
11764:
11763:
11761:
11753:if and only if
11725:
11722:
11721:
11695:
11691:
11685:
11674:
11652:
11648:
11646:
11643:
11642:
11616:
11612:
11606:
11595:
11589:
11586:
11585:
11582:
11561:
11533:
11530:
11529:
11513:
11505:
11500:
11497:
11496:
11479:
11475:
11473:
11470:
11469:
11461:
11444:
11440:
11438:
11435:
11434:
11406:
11402:
11396:
11392:
11380:
11364:
11360:
11358:
11355:
11354:
11336:
11332:
11330:
11327:
11326:
11310:
11307:
11306:
11290:
11287:
11286:
11270:
11267:
11266:
11245:
11234:
11224:
11220:
11215:
11212:
11211:
11199:
11158:
11155:
11154:
11125:
11109:
11085:
11083:
11080:
11079:
11051:
11048:
11047:
11031:
11028:
11027:
11010:
11006:
11004:
11001:
11000:
10972:
10969:
10968:
10945:
10936:
10933:
10932:
10897:
10893:
10891:
10888:
10887:
10867:
10863:
10854:
10850:
10838:
10832:
10829:
10828:
10800:
10797:
10796:
10776:
10772:
10767:
10764:
10763:
10735:
10733:
10730:
10729:
10709:
10703:
10700:
10699:
10663:
10659:
10655:
10634:
10628:
10625:
10624:
10605:
10603:
10600:
10599:
10570:
10566:
10564:
10561:
10560:
10529:
10519:
10512:
10508:
10490:
10486:
10484:
10481:
10480:
10475:functions, see
10452:
10446:
10443:
10442:
10423:
10421:
10418:
10417:
10401:
10398:
10397:
10376:
10372:
10370:
10367:
10366:
10350:
10347:
10346:
10343:
10335:locally compact
10316:
10299:
10296:
10295:
10278:
10274:
10272:
10269:
10268:
10252:
10249:
10248:
10216:
10212:
10194:
10190:
10181:
10177:
10156:
10152:
10143:
10139:
10121:
10117:
10090:
10086:
10050:
10046:
10004:
10001:
10000:
9968:
9953:
9949:
9940:
9936:
9918:
9914:
9893:
9890:
9889:
9870:
9866:
9864:
9861:
9860:
9844:
9841:
9840:
9814:
9810:
9808:
9805:
9804:
9787:
9783:
9781:
9778:
9777:
9757:
9753:
9751:
9748:
9747:
9725:
9722:
9721:
9696:
9660:
9656:
9635:
9632:
9631:
9613:
9610:
9609:
9587:
9584:
9583:
9566:
9562:
9560:
9557:
9556:
9540:
9537:
9536:
9513:
9509:
9507:
9504:
9503:
9488:
9484:
9480:
9477:
9460:
9457:
9456:
9440:
9437:
9436:
9413:
9409:
9407:
9404:
9403:
9374:
9370:
9368:
9365:
9364:
9344:
9340:
9335:
9332:
9331:
9315:
9312:
9311:
9295:
9292:
9291:
9287:
9265:
9262:
9261:
9244:
9240:
9238:
9235:
9234:
9214:
9211:
9210:
9175:
9171:
9169:
9166:
9165:
9141:
9138:
9137:
9121:
9118:
9117:
9084:
9080:
9078:
9075:
9074:
9067:
9061:
9056:
9026:
9022:
9017:
9014:
9013:
8997:
8994:
8993:
8973:
8970:
8969:
8925:
8921:
8903:
8899:
8897:
8894:
8893:
8869:
8865:
8860:
8857:
8856:
8836:
8833:
8832:
8804:
8781:
8778:
8777:
8760:
8756:
8748:
8745:
8744:
8724:
8720:
8712:
8709:
8708:
8691:
8687:
8685:
8682:
8681:
8648:
8643:
8631:
8602:
8594:
8592:
8584:
8580:
8568:
8564:
8562:
8550:
8535:
8531:
8519:
8515:
8513:
8501:
8495:
8492:
8491:
8464:
8460:
8454:
8443:
8437:
8434:
8433:
8406:
8400:
8396:
8393:
8384:
8380:
8378:
8375:
8374:
8350:
8344:
8340:
8338:
8325:
8318:
8313:
8312:
8304:
8303:
8301:
8284:
8278:
8274:
8272:
8268:
8266:
8263:
8262:
8236:
8232:
8214:
8210:
8193:
8187:
8183:
8181:
8177:
8175:
8172:
8171:
8151:
8147:
8145:
8142:
8141:
8124:
8120:
8118:
8115:
8114:
8091:
8088:
8087:
8070:
8066:
8064:
8061:
8060:
8033:
8027:
8023:
8021:
8015:
8004:
7998:
7995:
7994:
7971:
7968:
7967:
7950:
7946:
7940:
7934:
7931:
7930:
7913:
7909:
7903:
7897:
7894:
7893:
7853:
7850:
7849:
7827:
7824:
7823:
7806:
7802:
7794:
7779:
7775:
7770:
7768:
7765:
7764:
7747:
7743:
7741:
7738:
7737:
7721:
7706:
7702:
7700:
7697:
7696:
7676:
7672:
7667:
7664:
7663:
7636:
7628:
7625:
7624:
7617:
7595:
7591:
7579:
7573:
7570:
7569:
7531:
7527:
7518:
7514:
7512:
7509:
7508:
7478:
7474:
7472:
7469:
7468:
7445:
7441:
7429:
7425:
7420:
7417:
7416:
7387:
7383:
7371:
7367:
7352:
7346:
7343:
7342:
7305:
7302:
7301:
7285:
7282:
7281:
7265:
7262:
7261:
7226:
7222:
7220:
7217:
7216:
7182:
7179:
7178:
7145:
7132:
7112:
7097:
7083:
7079:
7078:
7074:
7073:
7072:
7068:
7051:
7047:
7029:
7025:
7016:
7012:
7011:
7007:
7005:
7002:
7001:
6977:
6973:
6969:
6961:
6946:
6942:
6940:
6937:
6936:
6919:
6915:
6913:
6910:
6909:
6893:
6890:
6889:
6867:
6864:
6863:
6829:
6826:
6825:
6803:
6773:
6769:
6764:
6762:
6759:
6758:
6742:
6739:
6738:
6716:
6705:
6702:
6701:
6682:
6667:
6663:
6654:
6650:
6648:
6645:
6644:
6609:
6605:
6603:
6600:
6599:
6583:
6580:
6579:
6554:
6524:
6520:
6515:
6513:
6510:
6509:
6487:
6484:
6483:
6449:
6446:
6445:
6426:
6423:
6422:
6400:
6397:
6396:
6374:
6371:
6370:
6354:
6351:
6350:
6334:
6331:
6330:
6314:
6311:
6310:
6294:
6291:
6290:
6274:
6271:
6270:
6236:
6233:
6232:
6209:
6205:
6203:
6200:
6199:
6179:
6176:
6175:
6159:
6156:
6155:
6127:
6107:
6104:
6103:
6081:
6078:
6077:
6055:
6025:
6021:
6016:
6014:
6011:
6010:
5988:
5985:
5984:
5950:
5947:
5946:
5930:
5927:
5926:
5879:
5875:
5873:
5870:
5869:
5822:
5818:
5816:
5813:
5812:
5790:
5787:
5786:
5764:
5761:
5760:
5737:
5736:
5725:
5716:
5715:
5689:
5676:
5675:
5657:
5653:
5641:
5620:
5617:
5616:
5597:
5594:
5593:
5571:
5568:
5567:
5547:
5543:
5538:
5535:
5534:
5518:
5515:
5514:
5494:
5493:
5487:
5483:
5465:
5461:
5458:
5457:
5415:
5411:
5404:
5403:
5401:
5398:
5397:
5375:
5371:
5366:
5363:
5362:
5335:
5331:
5319:
5315:
5300:
5294:
5291:
5290:
5257:
5225:
5213:
5200:
5196:
5161:
5158:
5157:
5109:
5106:
5105:
5104:when values of
5089:
5086:
5085:
5066:
5061:
5058:
5057:
5040:
5036:
5034:
5031:
5030:
5014:
5011:
5010:
4988:
4985:
4984:
4965:
4960:
4957:
4956:
4933:
4929:
4921:
4913:
4910:
4909:
4890:
4879:
4876:
4875:
4858:
4854:
4852:
4849:
4848:
4825:
4821:
4813:
4805:
4802:
4801:
4767:
4764:
4763:
4760:
4748:microcontinuity
4721:
4717:
4715:
4712:
4711:
4685:
4680:
4674:
4671:
4670:
4649:
4645:
4643:
4640:
4639:
4614:
4610:
4608:
4605:
4604:
4597:
4544:
4540:
4535:
4532:
4531:
4514:
4510:
4502:
4499:
4498:
4473:
4469:
4467:
4464:
4463:
4417:
4413:
4408:
4405:
4404:
4337:
4333:
4325:
4322:
4321:
4305:
4275:
4271:
4266:
4264:
4261:
4260:
4259:, by replacing
4237:
4235:Generalizations
4216:
4213:
4212:
4196:
4193:
4192:
4176:
4173:
4172:
4156:
4153:
4152:
4136:
4133:
4132:
4095:
4092:
4091:
4075:
4072:
4071:
4049:
4046:
4045:
4029:
4026:
4025:
4009:
4006:
4005:
3974:
3971:
3970:
3950:
3947:
3946:
3924:
3921:
3920:
3882:
3879:
3878:
3847:
3844:
3843:
3842:(i.e., between
3827:
3824:
3823:
3804:
3801:
3800:
3778:
3775:
3774:
3757:
3753:
3751:
3748:
3747:
3731:
3723:
3720:
3719:
3697:
3694:
3693:
3677:
3674:
3673:
3656:
3652:
3650:
3647:
3646:
3643:
3598:
3595:
3594:
3574:
3570:
3565:
3562:
3561:
3539:
3536:
3535:
3513:
3510:
3509:
3489:
3486:
3485:
3469:
3466:
3465:
3443:
3436:
3432:
3426:
3422:
3417:
3414:
3413:
3377:
3373:
3350:
3346:
3344:
3341:
3340:
3336:Symbolically,
3315:
3283:
3271:
3244:
3241:
3240:
3210:
3205:
3204:
3202:
3199:
3198:
3177:
3170:
3166:
3160:
3156:
3151:
3148:
3147:
3131:
3128:
3127:
3109:
3102:
3098:
3092:
3088:
3083:
3080:
3079:
3057:
3054:
3053:
3030:
3026:
3024:
3021:
3020:
3004:
3001:
3000:
2983:
2979:
2977:
2974:
2973:
2951:
2921:
2917:
2912:
2900:
2887:
2883:
2881:
2878:
2877:
2848:
2833:
2829:
2811:
2807:
2802:
2768:
2765:
2764:
2745:
2742:
2741:
2719:
2716:
2715:
2699:
2696:
2695:
2677:
2670:
2666:
2660:
2656:
2651:
2648:
2647:
2623:
2621:
2618:
2617:
2592:
2589:
2588:
2547:
2543:
2541:
2538:
2537:
2515:
2512:
2511:
2495:
2492:
2491:
2471:
2468:
2467:
2444:
2440:
2438:
2435:
2434:
2391:
2378:
2374:
2372:
2369:
2368:
2342:
2338:
2326:
2309:
2277:
2272:
2266:
2262:
2246:
2242:
2229:
2203:
2201:
2185:
2181:
2179:
2176:
2175:
2156:
2153:
2152:
2135:
2131:
2129:
2126:
2125:
2097:
2067:
2063:
2058:
2056:
2053:
2052:
2028:
2025:
2024:
2002:
1999:
1998:
1982:
1979:
1978:
1953:
1950:
1949:
1933:
1919:
1916:
1915:
1899:
1896:
1895:
1873:
1866:
1862:
1856:
1852:
1847:
1844:
1843:
1825:
1818:
1814:
1808:
1804:
1799:
1796:
1795:
1775:
1772:
1771:
1749:
1666:
1663:
1662:
1646:
1643:
1642:
1604:
1600:
1594:
1583:
1577:
1574:
1573:
1547:
1526:
1523:
1522:
1490:
1486:
1484:
1481:
1480:
1450:
1420:
1416:
1411:
1409:
1406:
1405:
1383:
1380:
1379:
1363:
1360:
1359:
1343:
1340:
1339:
1317:
1314:
1313:
1288:
1285:
1284:
1268:
1265:
1264:
1238:
1234:
1232:
1229:
1228:
1211:
1208:
1207:
1186:
1183:
1182:
1165:
1162:
1161:
1145:
1142:
1141:
1104:
1101:
1100:
1078:
1075:
1074:
1058:
1055:
1054:
1037:
1033:
1031:
1028:
1027:
1004:
1001:
1000:
977:
947:
943:
938:
936:
933:
932:
910:
907:
906:
889:
886:
885:
884:independent of
867:
864:
863:
832:
829:
828:
806:
803:
802:
786:
783:
782:
766:
763:
762:
746:
743:
742:
717:
714:
713:
687:
683:
681:
678:
677:
661:
658:
657:
641:
638:
637:
620:
616:
614:
611:
610:
594:
591:
590:
573:
569:
567:
564:
563:
547:
544:
543:
525:
522:
521:
503:
500:
499:
483:
480:
479:
450:
446:
431:
427:
418:
414:
412:
409:
408:
392:
389:
388:
372:
369:
368:
352:
349:
348:
332:
329:
328:
305:
301:
296:
293:
292:
232:
228:
210:
206:
204:
201:
200:
168:
165:
164:
148:
145:
144:
127:
123:
121:
118:
117:
101:
98:
97:
81:
78:
77:
61:
58:
57:
37:
33:
28:
25:
24:
17:
12:
11:
5:
13155:
13145:
13144:
13139:
13134:
13129:
13112:
13111:
13109:
13108:
13097:
13094:
13093:
13091:
13090:
13085:
13080:
13075:
13070:
13065:
13059:
13057:
13051:
13050:
13048:
13047:
13042:
13040:Fourier series
13037:
13032:
13027:
13025:Puiseux series
13022:
13020:Laurent series
13017:
13012:
13007:
13001:
12999:
12995:
12994:
12991:
12990:
12988:
12987:
12982:
12977:
12972:
12967:
12962:
12957:
12952:
12947:
12942:
12936:
12934:
12930:
12929:
12927:
12926:
12921:
12916:
12911:
12905:
12903:
12896:
12892:
12891:
12888:
12887:
12885:
12884:
12879:
12874:
12868:
12866:
12862:
12861:
12859:
12858:
12853:
12848:
12843:
12837:
12835:
12828:
12824:
12823:
12821:
12820:
12815:
12810:
12804:
12802:
12798:
12797:
12790:
12788:
12785:
12784:
12782:
12781:
12780:
12779:
12769:
12764:
12759:
12754:
12749:
12744:
12739:
12734:
12729:
12723:
12721:
12710:
12709:
12707:
12706:
12701:
12696:
12691:
12686:
12681:
12676:
12671:
12666:
12660:
12658:
12651:
12645:
12644:
12633:
12632:
12625:
12618:
12610:
12604:
12603:
12578:
12577:
12573:
12572:External links
12570:
12569:
12568:
12563:William Wade,
12561:
12550:Gerald Folland
12547:
12537:
12520:
12502:
12482:
12479:
12476:
12475:
12460:
12453:
12426:
12419:
12397:
12386:(4): 453–480.
12369:
12368:
12366:
12363:
12362:
12361:
12356:
12354:Dini's theorem
12351:
12346:
12339:
12336:
12295:
12291:
12287:
12284:
12264:
12259:
12255:
12251:
12231:
12209:
12205:
12184:
12181:
12178:
12154:
12149:
12145:
12141:
12118:
12115:
12109:
12103:
12074:
12070:
12064:
12059:
12056:
12053:
12049:
12030:
12015:
12012:
12009:
12006:
12003:
12000:
11997:
11981:
11956:
11952:
11946:
11941:
11938:
11935:
11931:
11927:
11924:
11912:
11903:
11892:
11881:
11880:
11868:
11865:
11862:
11841:
11835:
11831:
11826:
11820:
11815:
11812:
11809:
11805:
11791:absolutely on
11789:
11777:
11774:
11771:
11757:
11747:
11735:
11732:
11729:
11709:
11706:
11703:
11698:
11694:
11688:
11683:
11680:
11677:
11673:
11669:
11666:
11663:
11660:
11655:
11651:
11634:
11619:
11615:
11609:
11604:
11601:
11598:
11594:
11581:
11578:
11560:
11559:To analyticity
11557:
11537:
11516:
11512:
11508:
11504:
11482:
11478:
11447:
11443:
11426:
11425:
11414:
11409:
11405:
11399:
11395:
11389:
11386:
11383:
11379:
11375:
11372:
11367:
11363:
11339:
11335:
11314:
11294:
11274:
11248:
11243:
11240:
11237:
11233:
11227:
11223:
11219:
11198:
11195:
11194:
11193:
11180:
11177:
11174:
11171:
11168:
11165:
11162:
11142:
11139:
11136:
11132:
11128:
11124:
11118:
11115:
11112:
11108:
11104:
11101:
11098:
11095:
11091:
11088:
11067:
11064:
11061:
11058:
11055:
11035:
11013:
11009:
10988:
10985:
10982:
10979:
10976:
10956:
10952:
10948:
10944:
10940:
10920:
10917:
10914:
10911:
10908:
10905:
10900:
10896:
10875:
10870:
10866:
10862:
10857:
10853:
10847:
10844:
10841:
10837:
10816:
10813:
10810:
10807:
10804:
10784:
10779:
10775:
10771:
10745:
10741:
10738:
10716:
10712:
10708:
10687:
10684:
10681:
10678:
10675:
10670:
10666:
10662:
10658:
10654:
10651:
10648:
10645:
10641:
10637:
10633:
10611:
10608:
10587:
10584:
10581:
10578:
10573:
10569:
10547:
10544:
10541:
10538:
10535:
10532:
10526:
10522:
10518:
10515:
10511:
10507:
10504:
10501:
10498:
10493:
10489:
10459:
10455:
10451:
10429:
10426:
10405:
10394:differentiable
10379:
10375:
10354:
10342:
10339:
10321:Fourier series
10304:
10281:
10277:
10256:
10233:
10230:
10227:
10224:
10219:
10215:
10211:
10208:
10205:
10202:
10197:
10193:
10189:
10184:
10180:
10176:
10173:
10170:
10167:
10164:
10159:
10155:
10151:
10146:
10142:
10138:
10135:
10132:
10129:
10124:
10120:
10116:
10113:
10110:
10107:
10104:
10101:
10098:
10093:
10089:
10085:
10082:
10079:
10076:
10073:
10070:
10067:
10064:
10061:
10058:
10053:
10049:
10045:
10042:
10039:
10036:
10033:
10030:
10027:
10024:
10021:
10017:
10014:
10011:
10008:
9976:
9973:
9967:
9964:
9961:
9956:
9952:
9948:
9943:
9939:
9935:
9932:
9929:
9926:
9921:
9917:
9913:
9910:
9906:
9903:
9900:
9897:
9873:
9869:
9848:
9825:
9822:
9817:
9813:
9790:
9786:
9760:
9756:
9735:
9732:
9729:
9704:
9701:
9695:
9692:
9689:
9686:
9683:
9680:
9677:
9674:
9671:
9668:
9663:
9659:
9655:
9652:
9648:
9645:
9642:
9639:
9617:
9597:
9594:
9591:
9569:
9565:
9544:
9524:
9521:
9516:
9512:
9497:
9464:
9444:
9424:
9421:
9416:
9412:
9391:
9388:
9385:
9382:
9377:
9373:
9352:
9347:
9343:
9339:
9319:
9299:
9282:
9269:
9247:
9243:
9218:
9198:
9195:
9192:
9189:
9186:
9183:
9178:
9174:
9145:
9125:
9101:
9098:
9095:
9092:
9087:
9083:
9063:Main article:
9060:
9057:
9055:
9052:
9051:
9050:
9047:equicontinuous
9034:
9029:
9025:
9021:
9001:
8990:Dini's theorem
8977:
8945:
8942:
8939:
8934:
8931:
8928:
8924:
8920:
8917:
8914:
8911:
8906:
8902:
8877:
8872:
8868:
8864:
8840:
8829:
8822:
8815:
8808:
8803:
8800:
8788:
8785:
8763:
8759:
8755:
8752:
8732:
8727:
8723:
8719:
8716:
8694:
8690:
8678:
8677:
8666:
8663:
8657:
8654:
8651:
8647:
8640:
8637:
8634:
8630:
8626:
8620:
8617:
8614:
8611:
8608:
8605:
8600:
8597:
8587:
8583:
8577:
8574:
8571:
8567:
8559:
8556:
8553:
8549:
8545:
8538:
8534:
8528:
8525:
8522:
8518:
8510:
8507:
8504:
8500:
8467:
8463:
8457:
8452:
8449:
8446:
8442:
8419:
8412:
8409:
8403:
8399:
8392:
8387:
8383:
8371:
8370:
8356:
8353:
8347:
8343:
8337:
8331:
8328:
8321:
8316:
8311:
8307:
8300:
8296:
8290:
8287:
8281:
8277:
8271:
8256:
8255:
8244:
8239:
8235:
8231:
8228:
8225:
8222:
8217:
8213:
8209:
8205:
8199:
8196:
8190:
8186:
8180:
8154:
8150:
8127:
8123:
8098:
8095:
8073:
8069:
8057:
8056:
8045:
8039:
8036:
8030:
8026:
8018:
8013:
8010:
8007:
8003:
7975:
7953:
7949:
7943:
7939:
7916:
7912:
7906:
7902:
7881:
7878:
7875:
7872:
7869:
7866:
7863:
7860:
7857:
7837:
7834:
7831:
7809:
7805:
7801:
7797:
7793:
7790:
7787:
7782:
7778:
7773:
7750:
7746:
7724:
7720:
7717:
7714:
7709:
7705:
7684:
7679:
7675:
7671:
7639:
7635:
7632:
7616:
7613:
7598:
7594:
7588:
7585:
7582:
7578:
7557:
7554:
7551:
7548:
7545:
7542:
7539:
7534:
7530:
7526:
7521:
7517:
7489:
7486:
7481:
7477:
7456:
7453:
7448:
7444:
7440:
7437:
7432:
7428:
7424:
7413:
7412:
7401:
7398:
7395:
7390:
7386:
7382:
7379:
7374:
7370:
7366:
7361:
7358:
7355:
7351:
7327:
7324:
7321:
7318:
7315:
7312:
7309:
7289:
7269:
7249:
7246:
7243:
7240:
7237:
7229:
7225:
7204:
7201:
7198:
7195:
7192:
7189:
7186:
7175:
7174:
7163:
7160:
7157:
7152:
7149:
7144:
7139:
7136:
7131:
7127:
7123:
7120:
7115:
7110:
7104:
7101:
7095:
7090:
7087:
7082:
7077:
7071:
7067:
7063:
7059:
7054:
7050:
7046:
7043:
7040:
7037:
7032:
7028:
7024:
7019:
7015:
7010:
6984:
6980:
6976:
6972:
6968:
6964:
6960:
6957:
6954:
6949:
6945:
6922:
6918:
6897:
6877:
6874:
6871:
6851:
6848:
6845:
6842:
6839:
6836:
6833:
6813:
6810:
6806:
6802:
6799:
6796:
6793:
6790:
6787:
6784:
6781:
6776:
6772:
6767:
6746:
6726:
6723:
6719:
6715:
6712:
6709:
6689:
6685:
6681:
6678:
6675:
6670:
6666:
6662:
6657:
6653:
6632:
6629:
6626:
6623:
6620:
6617:
6612:
6608:
6587:
6567:
6564:
6561:
6557:
6553:
6550:
6547:
6544:
6541:
6538:
6535:
6532:
6527:
6523:
6518:
6497:
6494:
6491:
6471:
6468:
6465:
6462:
6459:
6456:
6453:
6433:
6430:
6410:
6407:
6404:
6378:
6358:
6338:
6318:
6298:
6278:
6258:
6255:
6252:
6249:
6246:
6243:
6240:
6220:
6217:
6212:
6208:
6183:
6163:
6143:
6140:
6137:
6134:
6130:
6126:
6123:
6120:
6117:
6114:
6111:
6091:
6088:
6085:
6065:
6062:
6058:
6054:
6051:
6048:
6045:
6042:
6039:
6036:
6033:
6028:
6024:
6019:
5998:
5995:
5992:
5972:
5969:
5966:
5963:
5960:
5957:
5954:
5934:
5914:
5911:
5908:
5905:
5902:
5899:
5896:
5893:
5890:
5887:
5882:
5878:
5857:
5854:
5851:
5848:
5845:
5842:
5839:
5836:
5833:
5830:
5825:
5821:
5800:
5797:
5794:
5774:
5771:
5768:
5754:
5753:
5740:
5735:
5732:
5729:
5726:
5724:
5721:
5718:
5717:
5714:
5711:
5708:
5705:
5702:
5699:
5696:
5693:
5690:
5688:
5685:
5682:
5681:
5679:
5674:
5671:
5668:
5665:
5660:
5656:
5650:
5647:
5644:
5640:
5636:
5633:
5630:
5627:
5624:
5601:
5581:
5578:
5575:
5555:
5550:
5546:
5542:
5522:
5511:
5510:
5497:
5490:
5486:
5482:
5479:
5476:
5473:
5468:
5464:
5460:
5459:
5456:
5453:
5450:
5447:
5444:
5441:
5438:
5435:
5432:
5429:
5426:
5423:
5418:
5414:
5410:
5409:
5407:
5383:
5378:
5374:
5370:
5359:
5358:
5346:
5343:
5338:
5334:
5330:
5327:
5322:
5318:
5314:
5309:
5306:
5303:
5299:
5276:
5275:
5264:
5260:
5256:
5253:
5250:
5247:
5244:
5241:
5238:
5235:
5232:
5228:
5222:
5219:
5216:
5212:
5208:
5203:
5199:
5195:
5192:
5189:
5186:
5183:
5180:
5177:
5174:
5171:
5168:
5165:
5113:
5093:
5073:
5069:
5065:
5043:
5039:
5018:
4998:
4995:
4992:
4972:
4968:
4964:
4942:
4939:
4936:
4932:
4928:
4924:
4920:
4917:
4897:
4893:
4889:
4886:
4883:
4861:
4857:
4834:
4831:
4828:
4824:
4820:
4816:
4812:
4809:
4789:
4786:
4783:
4780:
4777:
4774:
4771:
4759:
4756:
4735:
4732:
4729:
4724:
4720:
4699:
4696:
4693:
4688:
4683:
4679:
4652:
4648:
4617:
4613:
4596:
4593:
4576:
4573:
4570:
4567:
4564:
4561:
4558:
4555:
4552:
4547:
4543:
4539:
4517:
4513:
4509:
4506:
4476:
4472:
4425:
4420:
4416:
4412:
4369:
4366:
4363:
4360:
4357:
4354:
4351:
4348:
4345:
4340:
4336:
4332:
4329:
4308:
4304:
4301:
4298:
4295:
4292:
4289:
4286:
4283:
4278:
4274:
4269:
4236:
4233:
4220:
4200:
4180:
4160:
4140:
4120:
4117:
4114:
4111:
4108:
4105:
4102:
4099:
4079:
4059:
4056:
4053:
4033:
4013:
3993:
3990:
3987:
3984:
3981:
3978:
3954:
3934:
3931:
3928:
3901:
3898:
3895:
3892:
3889:
3886:
3866:
3863:
3860:
3857:
3854:
3851:
3831:
3811:
3808:
3788:
3785:
3782:
3760:
3756:
3734:
3730:
3727:
3707:
3704:
3701:
3681:
3659:
3655:
3642:
3639:
3626:
3623:
3620:
3617:
3614:
3611:
3608:
3605:
3602:
3582:
3577:
3573:
3569:
3549:
3546:
3543:
3523:
3520:
3517:
3508:and for every
3493:
3473:
3460:is said to be
3446:
3442:
3439:
3435:
3429:
3425:
3421:
3410:
3409:
3397:
3394:
3391:
3388:
3385:
3380:
3376:
3372:
3369:
3365:
3361:
3358:
3353:
3349:
3334:
3333:
3322:
3318:
3314:
3311:
3308:
3305:
3302:
3299:
3296:
3293:
3290:
3286:
3280:
3277:
3274:
3270:
3266:
3263:
3260:
3257:
3254:
3251:
3248:
3229:uniform metric
3213:
3208:
3196:function space
3180:
3176:
3173:
3169:
3163:
3159:
3155:
3135:
3112:
3108:
3105:
3101:
3095:
3091:
3087:
3067:
3064:
3061:
3041:
3038:
3033:
3029:
3008:
2986:
2982:
2970:
2969:
2958:
2954:
2950:
2947:
2944:
2941:
2938:
2935:
2932:
2929:
2924:
2920:
2915:
2909:
2906:
2903:
2899:
2895:
2890:
2886:
2871:
2870:
2858:
2855:
2851:
2847:
2844:
2841:
2836:
2832:
2828:
2825:
2822:
2819:
2814:
2810:
2805:
2800:
2796:
2793:
2790:
2787:
2784:
2781:
2778:
2775:
2772:
2749:
2729:
2726:
2723:
2703:
2680:
2676:
2673:
2669:
2663:
2659:
2655:
2626:
2602:
2599:
2596:
2576:
2573:
2570:
2567:
2564:
2561:
2558:
2555:
2550:
2546:
2525:
2522:
2519:
2499:
2475:
2455:
2452:
2447:
2443:
2431:
2430:
2418:
2415:
2412:
2409:
2406:
2403:
2400:
2397:
2394:
2389:
2386:
2381:
2377:
2362:
2361:
2350:
2345:
2341:
2335:
2332:
2329:
2325:
2318:
2312:
2308:
2305:
2301:
2298:
2292:
2289:
2286:
2283:
2280:
2276:
2269:
2265:
2260:
2257:
2254:
2249:
2245:
2238:
2235:
2232:
2227:
2224:
2221:
2215:
2212:
2209:
2206:
2199:
2196:
2193:
2188:
2184:
2160:
2138:
2134:
2122:
2121:
2110:
2107:
2104:
2100:
2096:
2093:
2090:
2087:
2084:
2081:
2078:
2075:
2070:
2066:
2061:
2038:
2035:
2032:
2012:
2009:
2006:
1986:
1966:
1963:
1960:
1957:
1936:
1932:
1929:
1926:
1923:
1903:
1876:
1872:
1869:
1865:
1859:
1855:
1851:
1828:
1824:
1821:
1817:
1811:
1807:
1803:
1779:
1761:uniform spaces
1748:
1745:
1729:Hermann Hankel
1673:
1670:
1650:
1630:
1627:
1624:
1621:
1618:
1615:
1612:
1607:
1603:
1597:
1592:
1589:
1586:
1582:
1559:Fourier series
1546:
1543:
1530:
1493:
1489:
1460:
1457:
1453:
1449:
1446:
1443:
1440:
1437:
1434:
1431:
1428:
1423:
1419:
1414:
1393:
1390:
1387:
1367:
1347:
1327:
1324:
1321:
1301:
1298:
1295:
1292:
1272:
1252:
1249:
1246:
1241:
1237:
1215:
1190:
1169:
1149:
1129:
1126:
1123:
1120:
1117:
1114:
1111:
1108:
1088:
1085:
1082:
1062:
1040:
1036:
1014:
1011:
1008:
987:
984:
980:
976:
973:
970:
967:
964:
961:
958:
955:
950:
946:
941:
920:
917:
914:
893:
871:
851:
848:
845:
842:
839:
836:
816:
813:
810:
790:
770:
750:
730:
727:
724:
721:
701:
698:
695:
690:
686:
665:
645:
623:
619:
598:
576:
572:
551:
529:
519:at every point
507:
487:
467:
464:
459:
456:
453:
449:
445:
440:
437:
434:
430:
426:
421:
417:
396:
376:
356:
336:
313:
308:
304:
300:
249:
246:
243:
240:
235:
231:
227:
224:
221:
218:
213:
209:
181:
178:
175:
172:
152:
130:
126:
105:
85:
65:
45:
40:
36:
32:
15:
9:
6:
4:
3:
2:
13154:
13143:
13140:
13138:
13135:
13133:
13130:
13128:
13125:
13124:
13122:
13107:
13099:
13098:
13095:
13089:
13086:
13084:
13081:
13079:
13076:
13074:
13071:
13069:
13066:
13064:
13061:
13060:
13058:
13056:
13052:
13046:
13043:
13041:
13038:
13036:
13033:
13031:
13028:
13026:
13023:
13021:
13018:
13016:
13013:
13011:
13008:
13006:
13005:Taylor series
13003:
13002:
13000:
12996:
12986:
12983:
12981:
12978:
12976:
12973:
12971:
12968:
12966:
12963:
12961:
12958:
12956:
12953:
12951:
12948:
12946:
12943:
12941:
12938:
12937:
12935:
12931:
12925:
12922:
12920:
12917:
12915:
12912:
12910:
12907:
12906:
12904:
12900:
12897:
12893:
12883:
12880:
12878:
12875:
12873:
12870:
12869:
12867:
12863:
12857:
12854:
12852:
12849:
12847:
12844:
12842:
12839:
12838:
12836:
12832:
12829:
12825:
12819:
12816:
12814:
12811:
12809:
12806:
12805:
12803:
12799:
12794:
12778:
12775:
12774:
12773:
12770:
12768:
12765:
12763:
12760:
12758:
12755:
12753:
12750:
12748:
12745:
12743:
12740:
12738:
12735:
12733:
12730:
12728:
12725:
12724:
12722:
12718:
12711:
12705:
12702:
12700:
12697:
12695:
12694:Powers of two
12692:
12690:
12687:
12685:
12682:
12680:
12679:Square number
12677:
12675:
12672:
12670:
12667:
12665:
12662:
12661:
12659:
12655:
12652:
12650:
12646:
12642:
12638:
12631:
12626:
12624:
12619:
12617:
12612:
12611:
12608:
12601:
12598:
12597:
12596:
12593:
12589:
12588:
12583:
12576:
12575:
12562:
12559:
12558:0-471-31716-0
12555:
12551:
12548:
12541:
12538:
12536:
12535:0-387-19374-X
12532:
12524:
12521:
12518:
12514:
12506:
12503:
12500:
12499:0-486-66165-2
12496:
12488:
12485:
12484:
12472:
12471:
12464:
12456:
12450:
12446:
12442:
12441:
12436:
12435:Lakatos, Imre
12430:
12422:
12416:
12412:
12408:
12401:
12393:
12389:
12385:
12381:
12374:
12370:
12360:
12357:
12355:
12352:
12350:
12347:
12345:
12342:
12341:
12335:
12333:
12329:
12324:
12322:
12318:
12314:
12309:
12293:
12289:
12282:
12257:
12253:
12229:
12207:
12203:
12182:
12179:
12176:
12169:if for every
12168:
12147:
12143:
12131:
12127:
12124:
12123:measure space
12113:
12106:
12102:
12098:
12094:
12090:
12072:
12068:
12057:
12054:
12051:
12047:
12038:
12033:
12029:
12010:
12007:
12004:
11998:
11995:
11987:
11980:
11976:
11972:
11954:
11950:
11939:
11936:
11933:
11929:
11925:
11922:
11911:
11906:
11902:
11898:
11891:
11885:
11866:
11863:
11860:
11833:
11829:
11813:
11810:
11807:
11803:
11794:
11790:
11769:
11760:
11756:
11752:
11749:uniformly on
11748:
11733:
11730:
11727:
11704:
11696:
11692:
11686:
11681:
11678:
11675:
11671:
11667:
11661:
11653:
11649:
11640:
11637:pointwise on
11636:
11635:
11633:
11617:
11613:
11602:
11599:
11596:
11592:
11577:
11575:
11570:
11566:
11556:
11554:
11549:
11535:
11510:
11502:
11480:
11476:
11467:
11445:
11441:
11432:
11412:
11407:
11403:
11397:
11393:
11381:
11373:
11370:
11365:
11361:
11353:
11337:
11333:
11312:
11292:
11272:
11264:
11241:
11238:
11235:
11225:
11221:
11208:
11207:
11206:
11204:
11192:
11175:
11172:
11169:
11163:
11160:
11137:
11130:
11126:
11122:
11110:
11102:
11096:
11089:
11086:
11062:
11059:
11056:
11033:
11011:
11007:
10983:
10980:
10977:
10950:
10946:
10942:
10915:
10912:
10909:
10903:
10898:
10894:
10868:
10864:
10855:
10851:
10839:
10811:
10808:
10805:
10777:
10773:
10760:
10759:
10758:
10743:
10739:
10736:
10714:
10710:
10706:
10685:
10682:
10679:
10676:
10673:
10668:
10664:
10660:
10656:
10652:
10646:
10639:
10635:
10631:
10609:
10606:
10585:
10582:
10579:
10571:
10567:
10542:
10539:
10533:
10530:
10524:
10520:
10516:
10513:
10509:
10505:
10499:
10491:
10487:
10478:
10474:
10457:
10453:
10449:
10427:
10424:
10403:
10395:
10377:
10373:
10352:
10338:
10336:
10332:
10331:
10325:
10322:
10315:
10302:
10279:
10275:
10254:
10245:
10231:
10228:
10217:
10213:
10206:
10203:
10195:
10191:
10182:
10178:
10171:
10168:
10157:
10153:
10144:
10140:
10136:
10130:
10122:
10118:
10111:
10108:
10099:
10091:
10087:
10083:
10077:
10071:
10065:
10062:
10051:
10047:
10040:
10037:
10031:
10025:
10019:
10015:
10012:
10009:
9998:
9996:
9991:
9974:
9971:
9965:
9954:
9950:
9941:
9937:
9933:
9927:
9919:
9915:
9908:
9904:
9901:
9898:
9887:
9871:
9867:
9846:
9839:
9823:
9820:
9815:
9811:
9788:
9784:
9774:
9758:
9754:
9733:
9730:
9727:
9718:
9702:
9699:
9693:
9684:
9678:
9675:
9669:
9661:
9657:
9650:
9646:
9643:
9640:
9629:
9615:
9595:
9592:
9589:
9567:
9563:
9542:
9522:
9519:
9514:
9510:
9496:
9494:
9476:
9462:
9442:
9422:
9414:
9410:
9389:
9383:
9380:
9375:
9371:
9345:
9341:
9317:
9297:
9281:
9267:
9245:
9241:
9232:
9216:
9196:
9190:
9187:
9184:
9181:
9176:
9172:
9163:
9159:
9143:
9123:
9096:
9090:
9085:
9081:
9071:
9066:
9059:To continuity
9048:
9027:
9023:
8999:
8991:
8975:
8967:
8963:
8959:
8940:
8932:
8929:
8926:
8922:
8918:
8912:
8904:
8900:
8891:
8870:
8866:
8854:
8838:
8830:
8827:
8823:
8820:
8816:
8813:
8809:
8806:
8805:
8799:
8786:
8783:
8761:
8757:
8753:
8750:
8730:
8725:
8721:
8717:
8714:
8692:
8688:
8664:
8661:
8655:
8652:
8649:
8645:
8632:
8624:
8618:
8612:
8609:
8606:
8598:
8595:
8585:
8581:
8575:
8572:
8569:
8565:
8551:
8543:
8536:
8532:
8526:
8523:
8520:
8516:
8502:
8490:
8489:
8488:
8486:
8481:
8465:
8461:
8450:
8447:
8444:
8440:
8430:
8417:
8410:
8407:
8401:
8397:
8390:
8385:
8381:
8354:
8351:
8345:
8341:
8335:
8329:
8326:
8319:
8309:
8298:
8294:
8288:
8285:
8279:
8275:
8269:
8261:
8260:
8259:
8242:
8237:
8233:
8229:
8226:
8220:
8215:
8211:
8207:
8203:
8197:
8194:
8188:
8184:
8178:
8170:
8169:
8168:
8152:
8148:
8125:
8121:
8112:
8111:complex plane
8096:
8093:
8071:
8067:
8043:
8037:
8034:
8028:
8024:
8011:
8008:
8005:
8001:
7993:
7992:
7991:
7988:
7987:
7973:
7951:
7947:
7941:
7937:
7914:
7910:
7904:
7900:
7879:
7876:
7873:
7870:
7867:
7864:
7861:
7858:
7855:
7835:
7832:
7829:
7807:
7803:
7799:
7788:
7780:
7776:
7748:
7744:
7715:
7712:
7707:
7703:
7677:
7673:
7660:
7656:
7654:
7633:
7630:
7622:
7612:
7596:
7592:
7580:
7549:
7546:
7543:
7528:
7524:
7519:
7515:
7506:
7501:
7487:
7479:
7475:
7454:
7438:
7435:
7430:
7426:
7399:
7396:
7393:
7380:
7377:
7372:
7368:
7353:
7341:
7340:
7339:
7322:
7319:
7316:
7310:
7307:
7287:
7267:
7244:
7241:
7238:
7227:
7223:
7199:
7196:
7193:
7187:
7184:
7161:
7158:
7155:
7150:
7147:
7142:
7137:
7134:
7129:
7125:
7121:
7118:
7113:
7108:
7102:
7099:
7093:
7088:
7085:
7080:
7075:
7069:
7065:
7061:
7052:
7048:
7041:
7038:
7030:
7026:
7017:
7013:
7008:
7000:
6999:
6998:
6982:
6978:
6974:
6966:
6962:
6958:
6952:
6947:
6943:
6920:
6916:
6895:
6875:
6872:
6869:
6846:
6843:
6840:
6834:
6831:
6811:
6808:
6797:
6791:
6788:
6782:
6774:
6770:
6744:
6724:
6721:
6717:
6713:
6710:
6707:
6687:
6683:
6679:
6676:
6668:
6664:
6655:
6651:
6627:
6624:
6621:
6615:
6610:
6606:
6585:
6565:
6562:
6559:
6548:
6542:
6539:
6533:
6525:
6521:
6495:
6492:
6489:
6466:
6463:
6460:
6454:
6451:
6431:
6428:
6408:
6405:
6402:
6394:
6390:
6376:
6356:
6336:
6316:
6296:
6276:
6253:
6250:
6247:
6241:
6238:
6218:
6210:
6206:
6197:
6181:
6161:
6138:
6135:
6132:
6128:
6124:
6121:
6118:
6112:
6109:
6089:
6086:
6083:
6063:
6060:
6049:
6043:
6040:
6034:
6026:
6022:
5996:
5993:
5990:
5967:
5964:
5961:
5955:
5952:
5932:
5912:
5909:
5903:
5897:
5894:
5888:
5880:
5876:
5855:
5852:
5846:
5840:
5837:
5831:
5823:
5819:
5798:
5795:
5792:
5772:
5769:
5766:
5758:
5733:
5730:
5727:
5722:
5719:
5712:
5706:
5703:
5700:
5694:
5691:
5686:
5683:
5677:
5672:
5666:
5658:
5654:
5642:
5634:
5628:
5622:
5615:
5614:
5613:
5599:
5573:
5548:
5544:
5520:
5488:
5484:
5480:
5474:
5466:
5462:
5451:
5448:
5445:
5433:
5430:
5427:
5421:
5416:
5412:
5405:
5396:
5395:
5394:
5376:
5372:
5344:
5341:
5328:
5325:
5320:
5316:
5301:
5289:
5288:
5287:
5285:
5281:
5262:
5251:
5245:
5242:
5236:
5230:
5220:
5217:
5214:
5206:
5193:
5190:
5187:
5181:
5175:
5172:
5169:
5163:
5156:
5155:
5154:
5152:
5148:
5144:
5140:
5137:
5133:
5130:
5125:
5111:
5091:
5071:
5067:
5063:
5041:
5037:
5016:
4996:
4993:
4990:
4970:
4966:
4962:
4940:
4937:
4934:
4926:
4922:
4918:
4895:
4891:
4887:
4884:
4881:
4859:
4855:
4832:
4829:
4826:
4818:
4814:
4810:
4784:
4781:
4778:
4772:
4769:
4755:
4753:
4749:
4730:
4722:
4718:
4694:
4686:
4681:
4677:
4668:
4650:
4646:
4637:
4633:
4630:converges to
4615:
4611:
4602:
4592:
4590:
4568:
4562:
4559:
4553:
4545:
4541:
4515:
4511:
4507:
4504:
4496:
4492:
4474:
4470:
4461:
4457:
4454:
4450:
4446:
4442:
4438:
4418:
4414:
4402:
4401:uniform space
4398:
4394:
4390:
4387:of functions
4386:
4381:
4361:
4355:
4352:
4346:
4338:
4334:
4327:
4299:
4293:
4290:
4284:
4276:
4272:
4258:
4254:
4250:
4246:
4242:
4232:
4218:
4198:
4178:
4158:
4138:
4115:
4112:
4109:
4103:
4100:
4097:
4077:
4057:
4054:
4051:
4031:
4011:
3988:
3982:
3979:
3976:
3968:
3952:
3932:
3929:
3926:
3917:
3915:
3914:entire domain
3899:
3896:
3890:
3884:
3864:
3861:
3855:
3849:
3829:
3809:
3806:
3786:
3783:
3780:
3758:
3754:
3728:
3725:
3705:
3702:
3699:
3679:
3657:
3653:
3638:
3624:
3621:
3618:
3612:
3609:
3606:
3600:
3575:
3571:
3547:
3544:
3541:
3521:
3518:
3515:
3507:
3491:
3471:
3463:
3440:
3437:
3427:
3423:
3412:The sequence
3395:
3386:
3383:
3378:
3374:
3367:
3359:
3351:
3347:
3339:
3338:
3337:
3320:
3309:
3303:
3300:
3294:
3288:
3278:
3275:
3272:
3264:
3258:
3255:
3252:
3246:
3239:
3238:
3237:
3235:
3231:
3230:
3211:
3197:
3174:
3171:
3161:
3157:
3133:
3106:
3103:
3093:
3089:
3059:
3039:
3031:
3027:
3006:
2999:converges to
2984:
2980:
2956:
2945:
2939:
2936:
2930:
2922:
2918:
2907:
2904:
2901:
2893:
2888:
2884:
2876:
2875:
2874:
2856:
2853:
2842:
2834:
2830:
2826:
2820:
2812:
2808:
2794:
2791:
2788:
2785:
2782:
2779:
2776:
2773:
2770:
2763:
2762:
2761:
2747:
2727:
2724:
2721:
2701:
2674:
2671:
2661:
2657:
2645:
2641:
2614:
2594:
2571:
2565:
2556:
2548:
2544:
2523:
2520:
2517:
2497:
2489:
2473:
2453:
2445:
2441:
2387:
2379:
2375:
2367:
2366:
2365:
2348:
2343:
2339:
2327:
2316:
2306:
2303:
2299:
2296:
2290:
2267:
2263:
2258:
2255:
2252:
2247:
2243:
2230:
2197:
2194:
2186:
2182:
2174:
2173:
2172:
2158:
2136:
2132:
2108:
2105:
2102:
2091:
2085:
2082:
2076:
2068:
2064:
2051:
2050:
2049:
2036:
2033:
2030:
2010:
2007:
2004:
1984:
1964:
1961:
1958:
1955:
1948:if for every
1927:
1924:
1921:
1901:
1893:
1870:
1867:
1857:
1853:
1822:
1819:
1809:
1805:
1793:
1777:
1768:
1766:
1762:
1758:
1757:metric spaces
1754:
1744:
1742:
1741:Cesare Arzelà
1738:
1734:
1730:
1726:
1721:
1718:
1714:
1710:
1706:
1702:
1698:
1694:
1690:
1685:
1671:
1668:
1648:
1625:
1622:
1619:
1616:
1613:
1605:
1601:
1590:
1587:
1584:
1580:
1571:
1567:
1562:
1560:
1556:
1552:
1542:
1528:
1521:
1517:
1513:
1509:
1491:
1487:
1478:
1472:
1458:
1455:
1444:
1438:
1435:
1429:
1421:
1417:
1391:
1388:
1385:
1365:
1345:
1325:
1322:
1319:
1296:
1290:
1270:
1263:falls within
1247:
1239:
1235:
1226:
1213:
1205:
1202:) such that,
1201:
1188:
1167:
1147:
1124:
1121:
1118:
1112:
1109:
1106:
1086:
1083:
1080:
1060:
1038:
1034:
1025:
1012:
1009:
1006:
985:
982:
971:
965:
962:
956:
948:
944:
918:
915:
912:
904:
891:
869:
846:
840:
837:
834:
814:
811:
808:
788:
768:
748:
725:
719:
712:differs from
696:
688:
684:
663:
643:
621:
617:
596:
589:converges to
574:
570:
549:
542:
527:
520:
505:
485:
478:differs from
465:
462:
457:
454:
451:
447:
443:
438:
435:
432:
428:
424:
419:
415:
394:
374:
354:
334:
326:
306:
302:
291:
287:
283:
279:
275:
271:
267:
244:
238:
233:
229:
225:
219:
211:
207:
197:
179:
176:
173:
170:
150:
128:
124:
103:
83:
63:
38:
34:
21:
13010:Power series
12881:
12752:Lucas number
12704:Powers of 10
12684:Cubic number
12585:
12579:
12540:Walter Rudin
12516:
12487:Konrad Knopp
12468:
12463:
12439:
12429:
12410:
12400:
12383:
12379:
12373:
12325:
12310:
12166:
12129:
12125:
12120:
12104:
12100:
12096:
12092:
12088:
12036:
12031:
12027:
11985:
11978:
11974:
11970:
11909:
11904:
11900:
11896:
11889:
11887:
11883:
11792:
11758:
11754:
11750:
11638:
11584:We say that
11583:
11562:
11550:
11465:
11430:
11427:
11209:
11200:
10761:
10344:
10328:
10326:
10317:
10246:
9999:
9992:
9888:
9775:
9719:
9630:
9501:
9478:
9283:
9231:metric space
9115:
9054:Applications
8965:
8961:
8957:
8679:
8482:
8431:
8372:
8257:
8058:
7989:
7661:
7658:
7657:
7618:
7568:, the limit
7504:
7502:
7414:
7176:
6392:
6391:
6102:by choosing
5756:
5755:
5512:
5360:
5284:uniform norm
5277:
5151:uniform norm
5146:
5131:
5126:
4761:
4751:
4666:
4635:
4631:
4598:
4588:
4494:
4490:
4459:
4455:
4448:
4444:
4440:
4436:
4396:
4392:
4388:
4382:
4257:metric space
4252:
4248:
4244:
4240:
4238:
3918:
3913:
3644:
3506:metric space
3461:
3411:
3335:
3227:
2971:
2872:
2615:
2432:
2363:
2123:
2023:and for all
1891:
1769:
1750:
1743:and others.
1722:
1704:
1692:
1686:
1563:
1548:
1473:
1206:
1203:
1181:
998:
883:
540:
518:
324:
273:
266:mathematical
263:
12877:Conditional
12865:Convergence
12856:Telescoping
12841:Alternating
12757:Pell number
12505:G. H. Hardy
11632:converges:
10598:. Clearly,
9859:containing
5612:, given by
5286:topology:
5280:convergence
4439:with limit
3464:with limit
1914:with limit
1737:Ulisse Dini
1717:G. H. Hardy
387:, a number
13121:Categories
12902:Convergent
12846:Convergent
12481:References
11460:is within
10827:such that
10757:required:
9886:such that
9628:such that
9162:continuity
8966:continuous
8802:Properties
8743:and since
8485:ratio test
8086:of radius
7651:using the
7260:to within
6757:such that
6643:such that
6508:such that
6198:). Hence,
5983:and given
5925:, for all
4497:and every
3912:) for the
3560:such that
2760:such that
2510:: for all
1747:Definition
1508:continuity
1506:, such as
143:is in the
12933:Divergent
12851:Divergent
12713:Advanced
12689:Factorial
12637:Sequences
12592:EMS Press
12294:δ
12286:∖
12230:δ
12208:δ
12177:δ
12063:∞
12048:∑
12026:and each
11945:∞
11930:∑
11899:and each
11864:∈
11819:∞
11804:∑
11776:∞
11773:→
11731:∈
11672:∑
11608:∞
11593:∑
11580:To series
11555:instead.
11503:ε
11394:∫
11388:∞
11385:→
11362:∫
11265:interval
11247:∞
11164:∈
11117:∞
11114:→
10904:∈
10846:∞
10843:→
10677:
10583:≡
10577:⇉
10534:
10514:−
10303:◻
10232:ε
10229:≤
10063:≤
10013:∈
10007:∀
9972:ε
9966:≤
9902:∈
9896:∀
9821:∈
9731:≥
9700:ε
9694:≤
9644:∈
9638:∀
9590:ε
9520:∈
9420:⇉
9387:→
9194:→
9091:
8919:≤
8754:⊂
8718:∈
8639:∞
8636:→
8558:∞
8555:→
8509:∞
8506:→
8456:∞
8441:∑
8373:and take
8336:≤
8299:≤
8230:∈
8224:∀
8208:≤
8017:∞
8002:∑
7938:∑
7901:∑
7880:…
7833:∈
7800:≤
7719:→
7634:⊂
7587:∞
7584:→
7533:∞
7525:∈
7485:⇉
7452:→
7447:∞
7443:‖
7436:−
7423:‖
7389:∞
7385:‖
7378:−
7365:‖
7360:∞
7357:→
7311:∈
7268:ϵ
7242:≥
7188:∈
7159:ϵ
7119:−
7039:−
6997:. Since
6873:≥
6835:∈
6812:ϵ
6789:−
6708:ϵ
6616:∈
6563:ϵ
6560:≥
6540:−
6493:≥
6455:∈
6403:ϵ
6337:ϵ
6297:ϵ
6242:∈
6216:→
6182:ϵ
6142:⌉
6136:
6125:ϵ
6122:
6116:⌈
6087:≥
6076:whenever
6064:ϵ
6041:−
5991:ϵ
5956:∈
5695:∈
5649:∞
5646:→
5580:∞
5577:→
5440:→
5337:∞
5333:‖
5326:−
5313:‖
5308:∞
5305:→
5243:−
5218:∈
5202:∞
5198:‖
5191:−
5185:‖
5149:with the
4994:≥
4882:ϵ
4773:∈
4723:∗
4687:∗
4651:∗
4601:hyperreal
4546:α
4512:α
4508:≥
4505:α
4471:α
4453:entourage
4419:α
4291:−
4247:, where (
4199:ϵ
4139:ϵ
4110:ϵ
4078:ϵ
4055:∈
4012:ϵ
3989:ϵ
3930:∈
3900:ϵ
3865:ϵ
3862:−
3810:ϵ
3729:∈
3700:ϵ
3619:∩
3519:∈
3441:∈
3393:→
3364:⟺
3357:⇉
3301:−
3276:∈
3175:∈
3107:∈
3066:∞
3063:→
3037:→
2937:−
2905:∈
2857:ϵ
2827:−
2799:⟹
2792:≥
2774:∈
2722:ϵ
2675:∈
2601:∞
2598:→
2563:→
2521:∈
2451:→
2385:→
2334:∞
2331:→
2317:−
2275:⟶
2237:∞
2234:→
2192:⇉
2106:ϵ
2083:−
2034:∈
2008:≥
1956:ϵ
1931:→
1871:∈
1823:∈
1669:ψ
1649:ϕ
1626:ψ
1620:ϕ
1596:∞
1581:∑
1459:ϵ
1436:−
1389:≥
1323:≥
1312:whenever
1271:ϵ
1168:ϵ
1119:ϵ
1084:∈
1010:∈
986:ϵ
963:−
916:≥
870:ϵ
847:ϵ
812:∈
749:ϵ
636:approach
506:ϵ
466:…
375:ϵ
347:on a set
290:functions
268:field of
239:
174:≥
151:ϵ
84:ϵ
13127:Calculus
13106:Category
12872:Absolute
12523:Bourbaki
12437:(1976).
12338:See also
11569:analytic
11131:′
11090:′
10951:′
10740:′
10715:′
10640:′
10610:′
10473:analytic
10458:′
10428:′
9838:open set
9489:ε/3
9481:ε/3
9455:, then
9290:Suppose
8956:for all
7822:for all
7736:and let
7300:for all
6824:for all
5811:, since
5127:Given a
4758:Examples
4443: :
4395:, where
3234:supremum
1770:Suppose
1549:In 1821
999:for all
286:sequence
270:analysis
12882:Uniform
12594:, 2001
11305:, then
11263:compact
10999:, then
8853:compact
5282:in the
5143:complex
5136:bounded
4255:) is a
3194:in the
1545:History
1140:(i.e.,
882:but is
264:In the
12834:Series
12641:series
12556:
12533:
12497:
12451:
12417:
11563:Using
11462:ε
11078:, and
9582:. Let
9485:ε
9402:. If
9045:is an
7233:
5945:. For
4587:is in
2642:, the
2616:Since
2217:
1697:German
12777:array
12657:Basic
12365:Notes
12091:then
12039:. If
11973:then
11915:. If
9499:Proof
9229:is a
8964:) of
8888:is a
8851:is a
4983:when
4746:(see
4399:is a
4320:with
3773:with
3641:Notes
3504:is a
2972:then
2638:is a
1790:is a
1765:below
1763:(see
1520:limit
276:is a
12717:list
12639:and
12554:ISBN
12531:ISBN
12495:ISBN
12449:ISBN
12415:ISBN
12330:and
12180:>
11888:Let
11153:for
10392:are
9593:>
9502:Let
9156:are
9136:and
8960:and
8817:For
8483:The
7848:and
7662:Let
7143:>
6862:and
6809:<
6482:and
6406:>
6309:and
6061:<
5994:>
5868:and
5785:and
5139:real
4762:For
4385:nets
4211:and
4151:and
3877:and
3784:>
3703:>
3545:>
2854:<
2725:>
2103:<
1959:>
1794:and
1767:).
1711:and
1661:and
1456:<
1378:for
983:<
284:. A
12445:141
12388:doi
11984:in
11576:).
11378:lim
11210:If
11107:lim
11046:on
10836:lim
10762:If
10674:cos
10531:sin
10345:If
10267:at
9803:at
9773:).
9435:on
9260:to
9116:If
9082:sin
8831:If
8629:lim
8548:lim
8499:lim
8432:If
7892:If
7577:lim
7467:if
7350:lim
7280:of
6935:at
6133:log
6119:log
5639:lim
5566:as
5298:lim
5211:sup
5141:or
4493:in
4458:in
3484:if
3269:sup
3126:on
3052:as
2898:sup
2613:.)
2587:as
2490:on
2466:on
2324:lim
2151:to
1894:on
1890:is
1792:set
1715:.
1471:).
1283:of
1180:and
1053:to
288:of
230:sin
13123::
12590:,
12584:,
12542:,
12529:;
12525:;
12517:19
12515:,
12511:;
12507:,
12489:,
12447:.
12409:.
12384:32
12382:.
12334:.
10244:,
9997:,
9990:.
7655:.
7507:,
7500:.
6688:2.
6349:,
5734:1.
4754:.
4669:,
4530:,
4447:→
4391:→
4380:.
4251:,
4243:→
2536:,
1739:,
1735:,
1731:,
1699::
1510:,
1227:,
541:in
272:,
12719:)
12715:(
12629:e
12622:t
12615:v
12560:.
12501:.
12457:.
12423:.
12394:.
12390::
12290:E
12283:E
12263:)
12258:n
12254:f
12250:(
12204:E
12183:0
12167:E
12153:)
12148:n
12144:f
12140:(
12126:E
12112:.
12110:n
12105:n
12101:f
12097:E
12093:f
12089:E
12073:n
12069:f
12058:1
12055:=
12052:n
12037:E
12032:n
12028:f
12014:]
12011:b
12008:,
12005:a
12002:[
11999:=
11996:E
11986:E
11982:0
11979:x
11975:f
11971:E
11955:n
11951:f
11940:1
11937:=
11934:n
11926:=
11923:f
11913:0
11910:x
11905:n
11901:f
11897:E
11893:0
11890:x
11879:.
11867:E
11861:x
11840:|
11834:n
11830:f
11825:|
11814:1
11811:=
11808:n
11793:E
11788:.
11770:n
11759:n
11755:s
11751:E
11746:.
11734:E
11728:x
11708:)
11705:x
11702:(
11697:j
11693:f
11687:n
11682:1
11679:=
11676:j
11668:=
11665:)
11662:x
11659:(
11654:n
11650:s
11639:E
11618:n
11614:f
11603:1
11600:=
11597:n
11536:f
11515:|
11511:I
11507:|
11481:n
11477:f
11466:f
11446:n
11442:f
11431:n
11413:.
11408:n
11404:f
11398:I
11382:n
11374:=
11371:f
11366:I
11352::
11338:n
11334:f
11313:f
11293:f
11273:I
11242:1
11239:=
11236:n
11232:)
11226:n
11222:f
11218:(
11191:.
11179:]
11176:b
11173:,
11170:a
11167:[
11161:x
11141:)
11138:x
11135:(
11127:n
11123:f
11111:n
11103:=
11100:)
11097:x
11094:(
11087:f
11066:]
11063:b
11060:,
11057:a
11054:[
11034:f
11012:n
11008:f
10987:]
10984:b
10981:,
10978:a
10975:[
10955:)
10947:n
10943:f
10939:(
10919:]
10916:b
10913:,
10910:a
10907:[
10899:0
10895:x
10874:)
10869:0
10865:x
10861:(
10856:n
10852:f
10840:n
10815:]
10812:b
10809:,
10806:a
10803:[
10783:)
10778:n
10774:f
10770:(
10744:,
10737:f
10711:n
10707:f
10686:,
10683:x
10680:n
10669:2
10665:/
10661:1
10657:n
10653:=
10650:)
10647:x
10644:(
10636:n
10632:f
10607:f
10586:0
10580:f
10572:n
10568:f
10546:)
10543:x
10540:n
10537:(
10525:2
10521:/
10517:1
10510:n
10506:=
10503:)
10500:x
10497:(
10492:n
10488:f
10454:n
10450:f
10425:f
10404:f
10378:n
10374:f
10353:S
10294:.
10280:0
10276:x
10255:f
10226:)
10223:)
10218:0
10214:x
10210:(
10207:f
10204:,
10201:)
10196:0
10192:x
10188:(
10183:N
10179:f
10175:(
10172:d
10169:+
10166:)
10163:)
10158:0
10154:x
10150:(
10145:N
10141:f
10137:,
10134:)
10131:x
10128:(
10123:N
10119:f
10115:(
10112:d
10109:+
10106:)
10103:)
10100:x
10097:(
10092:N
10088:f
10084:,
10081:)
10078:x
10075:(
10072:f
10069:(
10066:d
10060:)
10057:)
10052:0
10048:x
10044:(
10041:f
10038:,
10035:)
10032:x
10029:(
10026:f
10023:(
10020:d
10016:U
10010:x
9975:3
9963:)
9960:)
9955:0
9951:x
9947:(
9942:N
9938:f
9934:,
9931:)
9928:x
9925:(
9920:N
9916:f
9912:(
9909:d
9905:U
9899:x
9872:0
9868:x
9847:U
9824:E
9816:0
9812:x
9789:N
9785:f
9759:N
9755:f
9734:N
9728:n
9703:3
9691:)
9688:)
9685:x
9682:(
9679:f
9676:,
9673:)
9670:x
9667:(
9662:N
9658:f
9654:(
9651:d
9647:E
9641:x
9616:N
9596:0
9568:0
9564:x
9543:f
9523:E
9515:0
9511:x
9463:f
9443:E
9423:f
9415:n
9411:f
9390:M
9384:E
9381::
9376:n
9372:f
9351:)
9346:n
9342:f
9338:(
9318:M
9298:E
9268:f
9246:n
9242:f
9217:M
9197:M
9191:E
9188::
9185:f
9182:,
9177:n
9173:f
9144:M
9124:E
9100:)
9097:x
9094:(
9086:n
9033:)
9028:n
9024:f
9020:(
9000:S
8976:f
8962:x
8958:n
8944:)
8941:x
8938:(
8933:1
8930:+
8927:n
8923:f
8916:)
8913:x
8910:(
8905:n
8901:f
8876:)
8871:n
8867:f
8863:(
8839:S
8828:.
8814:.
8787:.
8784:S
8762:R
8758:D
8751:S
8731:,
8726:R
8722:D
8715:z
8693:n
8689:M
8665:0
8662:=
8656:1
8653:+
8650:n
8646:R
8633:n
8625:=
8619:!
8616:)
8613:1
8610:+
8607:n
8604:(
8599:!
8596:n
8586:n
8582:R
8576:1
8573:+
8570:n
8566:R
8552:n
8544:=
8537:n
8533:M
8527:1
8524:+
8521:n
8517:M
8503:n
8466:n
8462:M
8451:0
8448:=
8445:n
8418:.
8411:!
8408:n
8402:n
8398:R
8391:=
8386:n
8382:M
8355:!
8352:n
8346:n
8342:R
8330:!
8327:n
8320:n
8315:|
8310:z
8306:|
8295:|
8289:!
8286:n
8280:n
8276:z
8270:|
8243:.
8238:R
8234:D
8227:z
8221:,
8216:n
8212:M
8204:|
8198:!
8195:n
8189:n
8185:z
8179:|
8153:n
8149:M
8126:n
8122:M
8097:,
8094:R
8072:R
8068:D
8044:.
8038:!
8035:n
8029:n
8025:z
8012:0
8009:=
8006:n
7986:.
7974:E
7952:n
7948:f
7942:n
7915:n
7911:M
7905:n
7877:,
7874:3
7871:,
7868:2
7865:,
7862:1
7859:=
7856:n
7836:E
7830:x
7808:n
7804:M
7796:|
7792:)
7789:x
7786:(
7781:n
7777:f
7772:|
7749:n
7745:M
7723:C
7716:E
7713::
7708:n
7704:f
7683:)
7678:n
7674:f
7670:(
7638:C
7631:S
7597:n
7593:f
7581:n
7556:)
7553:]
7550:1
7547:,
7544:0
7541:[
7538:(
7529:C
7520:n
7516:f
7505:n
7488:f
7480:n
7476:f
7455:0
7439:f
7431:n
7427:f
7400:,
7397:1
7394:=
7381:f
7373:n
7369:f
7354:n
7326:]
7323:1
7320:,
7317:0
7314:[
7308:x
7288:f
7248:)
7245:N
7239:n
7236:(
7228:n
7224:f
7203:]
7200:1
7197:,
7194:0
7191:[
7185:x
7162:,
7156:=
7151:4
7148:1
7138:2
7135:1
7130:=
7126:|
7122:0
7114:N
7109:]
7103:N
7100:1
7094:)
7089:2
7086:1
7081:(
7076:[
7070:|
7066:=
7062:|
7058:)
7053:0
7049:x
7045:(
7042:f
7036:)
7031:0
7027:x
7023:(
7018:N
7014:f
7009:|
6983:N
6979:/
6975:1
6971:)
6967:2
6963:/
6959:1
6956:(
6953:=
6948:0
6944:x
6921:N
6917:f
6896:N
6876:N
6870:n
6850:]
6847:1
6844:,
6841:0
6838:[
6832:x
6805:|
6801:)
6798:x
6795:(
6792:f
6786:)
6783:x
6780:(
6775:n
6771:f
6766:|
6745:N
6725:,
6722:4
6718:/
6714:1
6711:=
6684:/
6680:1
6677:=
6674:)
6669:0
6665:x
6661:(
6656:n
6652:f
6631:)
6628:1
6625:,
6622:0
6619:[
6611:0
6607:x
6586:n
6566:.
6556:|
6552:)
6549:x
6546:(
6543:f
6537:)
6534:x
6531:(
6526:n
6522:f
6517:|
6496:N
6490:n
6470:]
6467:1
6464:,
6461:0
6458:[
6452:x
6432:,
6429:N
6409:0
6377:x
6357:N
6317:x
6277:N
6257:]
6254:1
6251:,
6248:0
6245:[
6239:x
6219:f
6211:n
6207:f
6162:x
6139:x
6129:/
6113:=
6110:N
6090:N
6084:n
6057:|
6053:)
6050:x
6047:(
6044:f
6038:)
6035:x
6032:(
6027:n
6023:f
6018:|
5997:0
5971:)
5968:1
5965:,
5962:0
5959:(
5953:x
5933:n
5913:1
5910:=
5907:)
5904:1
5901:(
5898:f
5895:=
5892:)
5889:1
5886:(
5881:n
5877:f
5856:0
5853:=
5850:)
5847:0
5844:(
5841:f
5838:=
5835:)
5832:0
5829:(
5824:n
5820:f
5799:1
5796:=
5793:x
5773:0
5770:=
5767:x
5731:=
5728:x
5723:,
5720:1
5713:;
5710:)
5707:1
5704:,
5701:0
5698:[
5692:x
5687:,
5684:0
5678:{
5673:=
5670:)
5667:x
5664:(
5659:n
5655:f
5643:n
5635:=
5632:)
5629:x
5626:(
5623:f
5600:f
5574:n
5554:)
5549:n
5545:f
5541:(
5521:f
5489:n
5485:x
5481:=
5478:)
5475:x
5472:(
5467:n
5463:f
5455:]
5452:1
5449:,
5446:0
5443:[
5437:]
5434:1
5431:,
5428:0
5425:[
5422::
5417:n
5413:f
5406:{
5382:)
5377:n
5373:f
5369:(
5357:.
5345:0
5342:=
5329:f
5321:n
5317:f
5302:n
5263:.
5259:|
5255:)
5252:x
5249:(
5246:g
5240:)
5237:x
5234:(
5231:f
5227:|
5221:X
5215:x
5207:=
5194:g
5188:f
5182:=
5179:)
5176:g
5173:,
5170:f
5167:(
5164:d
5147:X
5132:X
5112:x
5092:n
5072:4
5068:/
5064:1
5042:n
5038:x
5017:x
4997:2
4991:n
4971:4
4967:/
4963:1
4941:n
4938:+
4935:x
4931:)
4927:2
4923:/
4919:1
4916:(
4896:4
4892:/
4888:1
4885:=
4860:n
4856:x
4833:n
4830:+
4827:x
4823:)
4819:2
4815:/
4811:1
4808:(
4788:)
4785:1
4782:,
4779:0
4776:[
4770:x
4752:x
4734:)
4731:x
4728:(
4719:f
4698:)
4695:x
4692:(
4682:n
4678:f
4667:n
4647:f
4636:x
4632:f
4616:n
4612:f
4589:V
4575:)
4572:)
4569:x
4566:(
4563:f
4560:,
4557:)
4554:x
4551:(
4542:f
4538:(
4516:0
4495:E
4491:x
4475:0
4460:X
4456:V
4449:X
4445:E
4441:f
4424:)
4415:f
4411:(
4397:X
4393:X
4389:E
4368:)
4365:)
4362:x
4359:(
4356:f
4353:,
4350:)
4347:x
4344:(
4339:n
4335:f
4331:(
4328:d
4307:|
4303:)
4300:x
4297:(
4294:f
4288:)
4285:x
4282:(
4277:n
4273:f
4268:|
4253:d
4249:M
4245:M
4241:E
4219:x
4179:N
4159:x
4119:)
4116:x
4113:,
4107:(
4104:N
4101:=
4098:N
4058:E
4052:x
4032:N
3992:)
3986:(
3983:N
3980:=
3977:N
3953:N
3933:E
3927:x
3897:+
3894:)
3891:x
3888:(
3885:f
3859:)
3856:x
3853:(
3850:f
3830:f
3807:2
3787:N
3781:n
3759:n
3755:f
3733:N
3726:N
3706:0
3680:f
3658:n
3654:f
3625:.
3622:E
3616:)
3613:r
3610:,
3607:x
3604:(
3601:B
3581:)
3576:n
3572:f
3568:(
3548:0
3542:r
3522:E
3516:x
3492:E
3472:f
3445:N
3438:n
3434:)
3428:n
3424:f
3420:(
3408:.
3396:0
3390:)
3387:f
3384:,
3379:n
3375:f
3371:(
3368:d
3360:f
3352:n
3348:f
3321:.
3317:|
3313:)
3310:x
3307:(
3304:g
3298:)
3295:x
3292:(
3289:f
3285:|
3279:E
3273:x
3265:=
3262:)
3259:g
3256:,
3253:f
3250:(
3247:d
3212:E
3207:R
3179:N
3172:n
3168:)
3162:n
3158:f
3154:(
3134:E
3111:N
3104:n
3100:)
3094:n
3090:f
3086:(
3060:n
3040:0
3032:n
3028:d
3007:f
2985:n
2981:f
2957:,
2953:|
2949:)
2946:x
2943:(
2940:f
2934:)
2931:x
2928:(
2923:n
2919:f
2914:|
2908:E
2902:x
2894:=
2889:n
2885:d
2869:.
2850:|
2846:)
2843:x
2840:(
2835:n
2831:f
2824:)
2821:x
2818:(
2813:m
2809:f
2804:|
2795:N
2789:n
2786:,
2783:m
2780:,
2777:E
2771:x
2748:N
2728:0
2702:E
2679:N
2672:n
2668:)
2662:n
2658:f
2654:(
2625:R
2595:n
2575:)
2572:x
2569:(
2566:f
2560:)
2557:x
2554:(
2549:n
2545:f
2524:E
2518:x
2498:E
2474:E
2454:f
2446:n
2442:f
2417:y
2414:l
2411:m
2408:r
2405:o
2402:f
2399:i
2396:n
2393:u
2388:f
2380:n
2376:f
2349:.
2344:n
2340:f
2328:n
2311:u
2307:=
2304:f
2300:,
2297:f
2291:.
2288:f
2285:i
2282:n
2279:u
2268:n
2264:f
2259:,
2256:f
2253:=
2248:n
2244:f
2231:n
2226:m
2223:i
2220:l
2214:f
2211:i
2208:n
2205:u
2198:,
2195:f
2187:n
2183:f
2159:f
2137:n
2133:f
2109:.
2099:|
2095:)
2092:x
2089:(
2086:f
2080:)
2077:x
2074:(
2069:n
2065:f
2060:|
2037:E
2031:x
2011:N
2005:n
1985:N
1965:,
1962:0
1935:R
1928:E
1925::
1922:f
1902:E
1875:N
1868:n
1864:)
1858:n
1854:f
1850:(
1827:N
1820:n
1816:)
1810:n
1806:f
1802:(
1778:E
1695:(
1672:.
1629:)
1623:,
1617:,
1614:x
1611:(
1606:n
1602:f
1591:1
1588:=
1585:n
1529:f
1492:n
1488:f
1452:|
1448:)
1445:x
1442:(
1439:f
1433:)
1430:x
1427:(
1422:n
1418:f
1413:|
1392:N
1386:n
1366:N
1346:x
1326:N
1320:n
1300:)
1297:x
1294:(
1291:f
1251:)
1248:x
1245:(
1240:n
1236:f
1214:x
1189:x
1148:N
1128:)
1125:x
1122:,
1116:(
1113:N
1110:=
1107:N
1087:E
1081:x
1061:f
1039:n
1035:f
1013:E
1007:x
979:|
975:)
972:x
969:(
966:f
960:)
957:x
954:(
949:n
945:f
940:|
919:N
913:n
892:x
850:)
844:(
841:N
838:=
835:N
815:E
809:x
789:N
769:n
729:)
726:x
723:(
720:f
700:)
697:x
694:(
689:n
685:f
664:E
644:f
622:n
618:f
597:f
575:n
571:f
550:E
528:x
486:f
463:,
458:2
455:+
452:N
448:f
444:,
439:1
436:+
433:N
429:f
425:,
420:N
416:f
395:N
355:E
335:f
312:)
307:n
303:f
299:(
248:)
245:x
242:(
234:n
226:=
223:)
220:x
217:(
212:n
208:f
180:.
177:N
171:n
129:n
125:f
104:N
64:f
44:)
39:n
35:f
31:(
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.