693:
20:
452:
443:
1748:, a one-to-one correspondence of the (canonical) cycle notation and the one-line notation of permutations. In the second problem, the survival probability is independent of the chosen strategy and equal to the survival probability in the original problem with the cycle-following strategy. Since an arbitrary strategy for the original problem can also be applied to the second problem, but cannot attain a higher survival probability there, the cycle-following strategy has to be optimal.
71:
into 50 drawers in any order. The drawers are closed again afterwards. If, during this search, every prisoner finds their number in one of the drawers, all prisoners are pardoned. If even one prisoner does not find their number, all prisoners die. Before the first prisoner enters the room, the prisoners may discuss strategy — but may not communicate once the first prisoner enters to look in the drawers. What is the prisoners' best strategy?
1282:
1886:
end, they just have to ensure that their assignment of prisoners' numbers to drawers constitutes a permutation with a cycle of length larger than 50. The prisoners in turn can counter this by agreeing among themselves on a specific random numbering of the drawers, provided that the director does not overhear this and does not bother to respond by replacing numbers in the boxes before the prisoners are let in.
2348:
2544:. Any individual prisoner has a 50% chance of finding their own number on an odd-numbered try. The main strategy will work for all the prisoners if the permutation of the prisoners contains only cycles of odd length. For 100 prisoners the probability that all will succeed using the main strategy is approximately 7.9589%, which is substantially better than the probability
46:. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival.
2029:
1217:
2371:
consecutively open two of the three doors. If they are successful, the doors are closed again and the second player enters the room. The second player may also open two of the three doors, but they cannot communicate with the first player in any form. What is the winning probability if both players act optimally?
191:). By starting with their own number, the prisoner guarantees they are on the specific cycle of drawers containing their number. The only question is whether any cycle is longer than fifty drawers - and only one cycle can possibly be too long, since at most one can comprise more than half of the total drawers.
1854:
At first, Gál and
Miltersen considered in their paper the case that the number of boxes is twice the number of team members while half of the boxes are empty. This is a more difficult problem since empty boxes lead nowhere and thus the cycle-following strategy cannot be applied. It is an open problem
683:
different ways depending on the starting number of the cycle. During the opening of the drawers using the above strategy, each prisoner follows a single cycle which always ends with their own number. In the case of eight prisoners, this cycle-following strategy is successful if and only if the length
70:
The director of a prison offers 100 death row prisoners, who are numbered from 1 to 100, a last chance. A room contains a cupboard with 100 drawers. The director randomly puts one prisoner's number in each closed drawer. The prisoners enter the room, one after another. Each prisoner may open and look
1862:
developed a strategy for team B based on the cycle-following strategy for a more general problem in which the fraction of empty boxes as well as the fraction of boxes each team member is allowed to open are variable. The winning probability still tends to zero in this case, but slower than suggested
1799:
numbers. The authors noted that the winning probability can be increased also in the case where the team members don't find their own numbers. If the given answer is the product of all the signs found and if the length of the longest cycle is half the (even) number of players plus one, then the team
1743:
In 2006, Eugene Curtin and Max
Warshauer gave a proof for the optimality of the cycle-following strategy. The proof is based on an equivalence to a related problem in which all prisoners are allowed to be present in the room and observe the opening of the drawers. Mathematically, this equivalence is
2352:
It is noteworthy that although we receive the same expected values, they are from very different distributions. With the second strategy, some prisoners are simply destined to die or live given a particular permutation, and with the first strategy (i.e., no strategy), there is "truly" a 1/2 chance
1885:
In case the prison director does not have to distribute the numbers into the drawers randomly, and realizes that the prisoners may apply the above-mentioned strategy and guesses the box numbering the prisoners will apply (such as numbers indicated on the boxes), they can foil the strategy. To this
2516:, which is optimal since the first player cannot have a higher winning probability than that. In a further variant, three prizes are hidden behind the three doors and three players have to independently find their assigned prizes with two tries. In this case the winning probability is also
2370:
Behind three closed doors a car, the car keys and a goat are randomly distributed. There are two players: the first player has to find the car, the second player the keys to the car. Only if both players are successful they may drive the car home. The first player enters the room and may
1772:). Every player of team B must guess their color correctly after opening half of the boxes for their team to win. Initially, Gál and Miltersen assumed that the winning probability quickly tends to zero with increasing number of players. However, Sven Skyum, a colleague at
2343:{\displaystyle (1-\ln(2))\cdot 1+\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}\left(1-{\frac {k}{n}}\right)=1-\ln(2)+\sum _{\lfloor n/2\rfloor +1}^{N}{\frac {1}{k}}-\sum _{k=\lfloor n/2\rfloor +1}^{N}{\frac {1}{n}}=1-\ln(2)+\ln(2)-{\frac {1}{2}}={\frac {1}{2}}}
199:
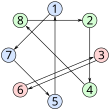
The reason this is a promising strategy is illustrated with the following example using 8 prisoners and drawers, whereby each prisoner may open 4 drawers. The prison director has distributed the prisoners' numbers into the drawers in the following fashion:
290:
In this case, all prisoners find their numbers. This is, however, not always the case. For example, the small change to the numbers of swapping drawers 5 and 8 would cause prisoner 1 to fail after opening 1, 7, 5, and 2 (and not finding their own number):
1040:
1726:
282:
Prisoner 4 opens drawers 4, 8, and 2, where they find their own number. This is the same cycle that was encountered by prisoner 2 and will be encountered by prisoner 8. Each of these prisoners will find their own number in the third opened
1776:, brought his attention to the cycle-following strategy for the case of this problem where there are no empty boxes. To find this strategy was left open as an exercise in the publication. The paper was honored with the best paper award.
1768:). In their version, player A (the prison director) randomly colors strips of paper with the names of the players of team B (the prisoners) in red or blue and puts each strip into a different box. Some of the boxes may be empty (see
1800:
members in this cycle either all guess wrong or all guess right. Even if this extension of the strategy offers a visible improvement for a small number of players, it becomes negligible when the number of players becomes large.
1017:
2400:
Player 2 first opens door 2. If the keys are behind the door, the player is successful. If the goat was behind the door, the player next opens door 3; whereas if the car was behind the door, the player next opens door
2396:
Player 1 first opens door 1. If the car is behind the door, the player is successful. If the keys were behind the door, the player next opens door 2; if instead the goat was behind the door, the player next opens door
1474:
158:
Surprisingly, there is a strategy that provides a survival probability of more than 30%. The key to success is that the prisoners do not have to decide beforehand which drawers to open. Each prisoner can use the
1898:, and then switch the contents of two boxes, all prisoners will survive. This is so since any cycle of length larger than 50 can be broken, so that it can be guaranteed that all cycles are of length at most 50.
684:
of the longest cycle of the permutation is at most 4. If a permutation contains a cycle of length 5 or more, all prisoners whose numbers lie in such a cycle do not reach their own number after four steps.
1984:
1595:
700:
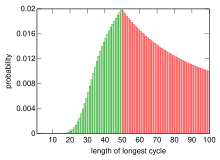
In the initial problem, the 100 prisoners are successful if the longest cycle of the permutation has a length of at most 50. Their survival probability is therefore equal to the probability that a
1863:
by Gál and
Miltersen. If the number of team members and the fraction of boxes which are opened is fixed, the winning probability stays strictly larger than zero when more empty boxes are added.
170:
To describe the strategy, not only the prisoners, but also the drawers, are numbered from 1 to 100; for example, row by row starting with the top left drawer. The strategy is now as follows:
1212:{\displaystyle 1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183,}
696:
Probability distribution of the length of the longest cycle of a random permutation of the numbers 1 to 100. The green area corresponds to the survival probability of the prisoners.
561:
1803:
In the following years, the problem entered the mathematical literature, where it was shaped in further different ways, for example with cards on a table or wallets in lockers (
772:
638:
163:
gained from the contents of every drawer they already opened to decide which one to open next. Another important observation is that this way the success of one prisoner is not
2022:
273:
Prisoner 1 first opens drawer 1 and finds number 7. Then they open drawer 7 and find number 5. Then they open drawer 5, where they find their own number and are successful.
1526:
1606:
474:
of the set of natural numbers from 1 to 100 to itself. A sequence of numbers which after repeated application of the permutation returns to the first number is called a
886:
2405:
In the six possible distributions of car, keys and goat behind the three doors, the players open the following doors (in the green cases, the player was successful):
1500:
912:
731:
811:
1247:
1994:
In the variant where any prisoner who finds their number is free, the expected probability of an individual's survival given a random permutation is as follows:
1310:
1919:
1330:
1267:
851:
831:
681:
661:
3031:
187:
If the prisoner could continue indefinitely this way, they would inevitably loop back to the drawer they started with, forming a permutation cycle (see
2500:
The success of the strategy is based on building a correlation between the successes and failures of the two players. Here, the winning probability is
920:
183:
The prisoner repeats steps 2 and 3 until they find their own number, or fail because the number is not found in the first fifty opened drawers.
1338:
1827:
in their textbooks on combinatorics. The problem, or riddle, along with a detailed explanation of the solution, was featured by the channel
460:
Graph representations of the permutations (1 7 5)(2 4 8)(3 6) and (1 3 7 4 5 8 2)(6)
3020:
2540:
Instead of having to find their number within the first 50 tries, the test could be finding the number within the 50 odd-numbered tries,
1921:, they can ensure their escape by opening significantly fewer than half of the drawers. Specifically, each prisoner needs to open only
2735:
1788:
3010:
1924:
2361:
In 2009, Adam S. Landsberg proposed the following simpler variant of the 100 prisoners problem which is based on the well-known
1533:
1735:, the prisoners survive with the cycle-following strategy in more than 30% of cases independently of the number of prisoners.
1285:
The harmonic numbers are approximately given by the area under the hyperbola and can therefore be approximated by a logarithm.
3085:
2994:
2976:
2951:
2939:
62:
360:
And in the following arrangement, prisoner 1 opens drawers 1, 3, 7, and 4, at which point they have to stop unsuccessfully:
566:
and thus consists of two cycles of length 3 and one cycle of length 2. The permutation of the third example is accordingly
2968:
704:
of the numbers 1 to 100 contains no cycle of length greater than 50. This probability is determined in the following.
643:
and consists of a cycle of length 7 and a cycle of length 1. The cycle notation is not unique since a cycle of length
180:
Otherwise, the drawer contains the number of another prisoner, and they next open the drawer labeled with this number.
3080:
164:
482:
cycles, that is, cycles which have no common elements. The permutation of the first example above can be written in
1023:
1332:
an arbitrary natural number, the prisoners' survival probability with the cycle-following strategy is given by
88:
that a single prisoner finds their number is 50%. The probability that all prisoners find their numbers is the
2572:
1480:
1859:
2577:
1819:
492:
736:
572:
3064:
3057:
3047:
2567:
1838:
1027:
167:
of the success of the other prisoners, because they all depend on the way the numbers are distributed.
1745:
23:
Each prisoner has to find their own number in one of 100 drawers, but may open only 50 of the drawers.
1874:
1809:
466:
The prison director's assignment of prisoner numbers to drawers can mathematically be described as a
276:
Prisoner 2 opens drawers 2, 4, and 8 in this order. In the last drawer they find their own number, 2.
2000:
1721:{\displaystyle \lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685.}
1273:. Therefore, using the cycle-following strategy the prisoners survive in a surprising 31% of cases.
1026:) random permutation contains no cycle of length greater than 50 is calculated with the formula for
2701:
1732:
77:
1756:
The 100 prisoners problem was first considered in 2003 by Anna Gál and Peter Bro
Miltersen in the
1505:
57:
The 100 prisoners problem has different renditions in the literature. The following version is by
2562:
1855:
whether in this case the winning probability tends to zero with growing number of team members.
2685:
Anna Gál, Peter Bro
Miltersen (2003), "The cell probe complexity of succinct data structures",
2601:
1757:
3017:
856:
3090:
2557:
1485:
891:
710:
89:
1807:). In the form of a prisoner problem it was posed in 2006 by Christoph Pöppe in the journal
781:
692:
1823:. With slight alterations this form was adopted by Philippe Flajolet, Robert Sedgewick and
1225:
888:
ways. Therefore, the number of permutations of the numbers 1 to 100 with a cycle of length
35:
8:
1031:
2687:
Proceedings 30th
International Colloquium on Automata, Languages and Programming (ICALP)
1292:
2960:
2853:
2789:
2641:
2362:
1904:
1824:
1796:
1315:
1252:
836:
816:
701:
666:
646:
475:
39:
2990:
2972:
2947:
2935:
2645:
1773:
58:
2912:
2884:
2781:
2633:
1792:
3024:
2793:
1780:
1270:
2815:
Third
International Conference on Quantum, Nano and Micro Technologies ICQNM '09
2548:
that would be obtained if each prisoner opened drawers independently at random.
2810:
1870:
483:
3051:
3041:
2917:
2889:
1832:
1012:{\displaystyle {\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}.}
707:
A permutation of the numbers 1 to 100 can contain at most one cycle of length
3074:
3037:
1814:
479:
43:
19:
2376:
If the players select their doors randomly, the winning probability is only
451:
442:
775:
467:
160:
85:
32:
286:
Prisoners 5 to 7 will also each find their numbers in a similar fashion.
177:
If this drawer contains their number, they are done and were successful.
2806:
2637:
1866:
1828:
1469:{\displaystyle 1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2.}
81:
2785:
853:
because of cyclic symmetry. The remaining numbers can be arranged in
471:
49:
Anna Gál and Peter Bro
Miltersen first proposed the problem in 2003.
2934:
2858:
2844:
2827:
2599:
1762:
30. International
Colloquium on Automata, Languages and Programming
279:
Prisoner 3 opens drawers 3 and 6, where they find their own number.
174:
Each prisoner first opens the drawer labeled with their own number.
3011:
Mathematicians hate civil liberties - 100 prisoners and 100 boxes
1281:
2736:"Mathematische Unterhaltungen: Freiheit für die Kombinatoriker"
1989:
1600:
holds, which results in an asymptotic survival probability of
145:, a vanishingly small number. The situation appears hopeless.
2684:
1765:
478:
of the permutation. Every permutation can be decomposed into
429:
Indeed, all prisoners except 6 (who succeeds directly) fail.
2772:
Navin Goyal, Michael Saks (2005), "A parallel search game",
2623:
1979:{\displaystyle O\left(N{\frac {\log \log N}{\log N}}\right)}
2699:
2392:(about 44%). The optimal strategy is, however, as follows:
2805:
2624:
Eugene Curtin, Max
Warshauer (2006), "The locker puzzle",
2965:
Algebraic Combinatorics: Walks, Trees, Tableaux, and More
2771:
2667:
Algebraic Combinatorics: Walks, Trees, Tableaux, and More
1590:{\displaystyle \lim _{n\to \infty }(H_{n}-\ln n)=\gamma }
1894:
In the case that one prisoner may enter the room first,
1779:
In spring 2004, the problem appeared in Joe Buhler and
778:). Within this cycle, these numbers can be arranged in
2875:
Adam S. Landsberg (2009), "The Return of Monty Hall",
741:
2032:
2003:
1927:
1907:
1609:
1536:
1508:
1488:
1341:
1318:
1295:
1255:
1228:
1043:
923:
894:
859:
839:
819:
784:
739:
713:
669:
649:
575:
495:
2846:
The Prisoners and the Swap: Less than Half is Enough
833:
permutations to represent distinct cycles of length
1889:
2959:
2664:
2342:
2016:
1978:
1913:
1720:
1589:
1520:
1494:
1468:
1324:
1304:
1261:
1241:
1211:
1011:
906:
880:
845:
825:
805:
766:
725:
675:
655:
632:
555:
2874:
2718:
940:
927:
470:of the numbers 1 to 100. Such a permutation is a
3072:
2903:Eric Grundwald (2010), "Re: The Locker Puzzle",
1611:
1538:
774:ways to select the numbers of such a cycle (see
2753:Peter Winkler (2006), "Names in Boxes Puzzle",
2733:
1986:drawers to secure the escape of all prisoners.
1312:instead of 100 prisoners are considered, where
188:
2902:
2984:
2842:
2752:
1901:For a sufficiently large number of prisoners
1877:variant in which team B wins with certainty.
757:
744:
432:
2870:
2868:
2828:Philippe Flajolet, Robert Sedgewick (2009),
2723:, Cambridge University Press, pp. 29–30
2600:Philippe Flajolet, Robert Sedgewick (2009),
2246:
2232:
2192:
2178:
2094:
2080:
2026:With the strategy for the original problem:
1990:Any prisoner who finds their number is free
3067:to check the optimal strategy, 6 July 2022
2595:
2593:
2916:
2888:
2865:
2857:
2832:, Cambridge University Press, p. 177
2680:
2678:
2676:
2660:
2658:
2656:
2654:
2606:, Cambridge University Press, p. 124
1880:
1791:. Thereby, the authors replaced boxes by
687:
2619:
2617:
2615:
2613:
1789:Mathematical Sciences Research Institute
1280:
691:
18:
2590:
2532:when the optimal strategy is employed.
1731:Since the sequence of probabilities is
3073:
2746:
2673:
2651:
2535:
92:of the single probabilities, which is
2813:(2009), "The quantum locker puzzle",
2721:Cryptography and Secure Communication
2693:
2610:
2356:
76:If every prisoner selects 50 drawers
2727:
2700:Joe Buhler, Elwyn Berlekamp (2004),
556:{\displaystyle (1~7~5)(2~4~8)(3~6)}
13:
2969:Undergraduate Texts in Mathematics
2774:Random Structures & Algorithms
1783:'s puzzle column of the quarterly
1621:
1548:
1515:
931:
767:{\displaystyle {\tbinom {100}{l}}}
748:
633:{\displaystyle (1~3~7~4~5~8~2)(6)}
269:The prisoners now act as follows:
14:
3102:
3003:
1890:One prisoner may make one change
1769:
450:
441:
2896:
2836:
2821:
2799:
1795:and colored strips of paper by
3065:Stochastic simulation in Julia
3053:Solution to The Impossible Bet
2946:, Cambridge University Press,
2765:
2712:
2311:
2305:
2293:
2287:
2167:
2161:
2057:
2054:
2048:
2033:
2017:{\displaystyle {\frac {1}{2}}}
1849:
1661:
1626:
1618:
1578:
1553:
1545:
1512:
1451:
1426:
1420:
1389:
1377:
1348:
1276:
1197:
1171:
982:
970:
961:
949:
872:
860:
797:
785:
627:
621:
618:
576:
550:
538:
535:
517:
514:
496:
1:
2928:
2583:
2573:Random permutation statistics
1738:
3086:Probability theory paradoxes
2742:(in German), 6/2006: 106–108
2669:, Springer, pp. 187–189
1521:{\displaystyle n\to \infty }
7:
2755:College Mathematics Journal
2665:Richard P. Stanley (2013),
2551:
1844:
1820:College Mathematics Journal
194:
153:
148:
10:
3107:
2905:Mathematical Intelligencer
2877:Mathematical Intelligencer
2719:Richard E. Blahut (2014),
2626:Mathematical Intelligencer
2568:Unexpected hanging paradox
1751:
433:Permutation representation
52:
2987:Mathematical Mind-Benders
2918:10.1007/s00283-009-9107-1
2890:10.1007/s00283-008-9016-8
2740:Spektrum der Wissenschaft
1858:In 2005, Navin Goyal and
1810:Spektrum der Wissenschaft
1481:Euler–Mascheroni constant
1022:The probability, that a (
3081:Recreational mathematics
2734:Christoph Pöppe (2006),
1746:Foata's transition lemma
1733:monotonically decreasing
881:{\displaystyle (100-l)!}
2578:Golomb–Dickman constant
2563:Three prisoners problem
2353:for every permutation.
1495:{\displaystyle \gamma }
907:{\displaystyle l>50}
726:{\displaystyle l>50}
2989:, Taylor and Francis,
2985:Peter Winkler (2007),
2944:Analytic Combinatorics
2843:Uri Mendlovic (2024),
2830:Analytic Combinatorics
2603:Analytic Combinatorics
2344:
2261:
2207:
2109:
2018:
1980:
1915:
1881:The malicious director
1722:
1591:
1522:
1496:
1470:
1326:
1306:
1286:
1263:
1243:
1213:
1013:
908:
882:
847:
827:
807:
806:{\displaystyle (l-1)!}
768:
727:
697:
688:Probability of success
677:
657:
634:
557:
24:
2345:
2221:
2173:
2069:
2019:
1981:
1916:
1873:considered in 2009 a
1723:
1592:
1523:
1497:
1471:
1327:
1307:
1284:
1264:
1244:
1242:{\displaystyle H_{n}}
1214:
1024:uniformly distributed
1014:
909:
883:
848:
828:
813:ways since there are
808:
769:
728:
695:
678:
658:
635:
558:
29:100 prisoners problem
22:
2030:
2001:
1925:
1905:
1607:
1534:
1506:
1486:
1339:
1316:
1293:
1253:
1226:
1041:
1032:complementary events
1030:and the formula for
921:
892:
857:
837:
817:
782:
737:
733:. There are exactly
711:
667:
647:
573:
493:
3034:, Spring 2011 (PDF)
2536:Odd number of tries
1875:quantum theoretical
397:number of prisoner
328:number of prisoner
237:number of prisoner
16:Mathematics problem
3032:Prisoners in Boxes
3030:Jamie Mulholland:
3027:, 12 December 2009
3023:2014-07-14 at the
3018:Pity the prisoners
2961:Richard P. Stanley
2761:(4): 260, 285, 289
2689:, pp. 332–344
2638:10.1007/BF02986999
2558:Prisoner's dilemma
2430:Goat − Keys − Car
2363:Monty Hall problem
2357:Monty Hall problem
2340:
2014:
1997:Without strategy:
1976:
1911:
1825:Richard P. Stanley
1718:
1625:
1587:
1552:
1518:
1492:
1466:
1322:
1305:{\displaystyle 2n}
1302:
1287:
1259:
1239:
1209:
1009:
904:
878:
843:
823:
803:
764:
762:
723:
702:random permutation
698:
673:
663:can be written in
653:
630:
553:
472:one-to-one mapping
40:probability theory
25:
3060:, 8 December 2014
3043:An Impossible Bet
3013:, 13 January 2014
2996:978-1-568-81336-3
2978:978-1-461-46998-8
2953:978-1-139-47716-1
2936:Philippe Flajolet
2786:10.1002/rsa.20068
2542:1, 3, ..., 97, 99
2496:
2495:
2427:Goat − Car − Keys
2424:Keys − Goat − Car
2421:Keys − Car − Goat
2418:Car − Goat − Keys
2415:Car − Keys − Goat
2338:
2325:
2270:
2216:
2139:
2118:
2012:
1969:
1914:{\displaystyle N}
1896:inspect all boxes
1774:Aarhus University
1610:
1537:
1325:{\displaystyle n}
1262:{\displaystyle n}
1155:
1136:
1107:
1083:
1063:
1004:
938:
846:{\displaystyle l}
826:{\displaystyle l}
755:
676:{\displaystyle l}
656:{\displaystyle l}
614:
608:
602:
596:
590:
584:
546:
531:
525:
510:
504:
425:
424:
368:number of drawer
356:
355:
299:number of drawer
265:
264:
208:number of drawer
59:Philippe Flajolet
3098:
3054:
3044:
2999:
2981:
2956:
2940:Robert Sedgewick
2922:
2921:
2920:
2900:
2894:
2893:
2892:
2872:
2863:
2862:
2861:
2851:
2840:
2834:
2833:
2825:
2819:
2818:
2817:, pp. 63–66
2803:
2797:
2796:
2769:
2763:
2762:
2750:
2744:
2743:
2731:
2725:
2724:
2716:
2710:
2709:
2708:, Spring 2004: 3
2702:"Puzzles Column"
2697:
2691:
2690:
2682:
2671:
2670:
2662:
2649:
2648:
2621:
2608:
2607:
2597:
2547:
2543:
2531:
2529:
2528:
2525:
2522:
2515:
2513:
2512:
2509:
2506:
2410:
2409:
2391:
2389:
2388:
2385:
2382:
2349:
2347:
2346:
2341:
2339:
2331:
2326:
2318:
2271:
2263:
2260:
2255:
2242:
2217:
2209:
2206:
2201:
2188:
2145:
2141:
2140:
2132:
2119:
2111:
2108:
2103:
2090:
2023:
2021:
2020:
2015:
2013:
2005:
1985:
1983:
1982:
1977:
1975:
1971:
1970:
1968:
1957:
1940:
1920:
1918:
1917:
1912:
1835:
1727:
1725:
1724:
1719:
1660:
1659:
1647:
1646:
1624:
1596:
1594:
1593:
1588:
1565:
1564:
1551:
1527:
1525:
1524:
1519:
1501:
1499:
1498:
1493:
1475:
1473:
1472:
1467:
1438:
1437:
1404:
1403:
1376:
1375:
1363:
1362:
1331:
1329:
1328:
1323:
1311:
1309:
1308:
1303:
1268:
1266:
1265:
1260:
1248:
1246:
1245:
1240:
1238:
1237:
1218:
1216:
1215:
1210:
1196:
1195:
1183:
1182:
1161:
1157:
1156:
1148:
1137:
1129:
1113:
1109:
1108:
1103:
1095:
1084:
1079:
1071:
1064:
1062:
1051:
1018:
1016:
1015:
1010:
1005:
1000:
992:
945:
944:
943:
930:
913:
911:
910:
905:
887:
885:
884:
879:
852:
850:
849:
844:
832:
830:
829:
824:
812:
810:
809:
804:
773:
771:
770:
765:
763:
761:
760:
747:
732:
730:
729:
724:
682:
680:
679:
674:
662:
660:
659:
654:
639:
637:
636:
631:
612:
606:
600:
594:
588:
582:
562:
560:
559:
554:
544:
529:
523:
508:
502:
454:
445:
392: 8
365:
364:
323: 8
296:
295:
232: 8
205:
204:
144:
143:
140:
137:
134:
131:
128:
125:
122:
119:
110:
108:
107:
104:
101:
63:Robert Sedgewick
3106:
3105:
3101:
3100:
3099:
3097:
3096:
3095:
3071:
3070:
3052:
3042:
3025:Wayback Machine
3006:
2997:
2979:
2954:
2931:
2926:
2925:
2901:
2897:
2873:
2866:
2849:
2841:
2837:
2826:
2822:
2804:
2800:
2770:
2766:
2751:
2747:
2732:
2728:
2717:
2713:
2698:
2694:
2683:
2674:
2663:
2652:
2622:
2611:
2598:
2591:
2586:
2554:
2545:
2541:
2538:
2526:
2523:
2520:
2519:
2517:
2510:
2507:
2504:
2503:
2501:
2489:(Door 1: Goat)
2488:
2483:
2482:(Door 2: Goat)
2478:
2473:
2460:
2455:
2450:
2445:
2386:
2383:
2380:
2379:
2377:
2359:
2330:
2317:
2262:
2256:
2238:
2225:
2208:
2202:
2184:
2177:
2131:
2124:
2120:
2110:
2104:
2086:
2073:
2031:
2028:
2027:
2004:
2002:
1999:
1998:
1992:
1958:
1941:
1939:
1935:
1931:
1926:
1923:
1922:
1906:
1903:
1902:
1892:
1883:
1852:
1847:
1833:
1781:Elwyn Berlekamp
1754:
1741:
1655:
1651:
1639:
1635:
1614:
1608:
1605:
1604:
1560:
1556:
1541:
1535:
1532:
1531:
1507:
1504:
1503:
1487:
1484:
1483:
1433:
1429:
1396:
1392:
1371:
1367:
1355:
1351:
1340:
1337:
1336:
1317:
1314:
1313:
1294:
1291:
1290:
1279:
1271:harmonic number
1254:
1251:
1250:
1233:
1229:
1227:
1224:
1223:
1191:
1187:
1178:
1174:
1147:
1128:
1127:
1123:
1096:
1094:
1072:
1070:
1069:
1065:
1055:
1050:
1042:
1039:
1038:
993:
991:
939:
926:
925:
924:
922:
919:
918:
893:
890:
889:
858:
855:
854:
838:
835:
834:
818:
815:
814:
783:
780:
779:
756:
743:
742:
740:
738:
735:
734:
712:
709:
708:
690:
668:
665:
664:
648:
645:
644:
574:
571:
570:
494:
491:
490:
464:
463:
462:
461:
457:
456:
455:
447:
446:
435:
389: 7
386: 6
383: 5
380: 4
377: 3
374: 2
371: 1
320: 7
317: 6
314: 5
311: 4
308: 3
305: 2
302: 1
229: 7
226: 6
223: 5
220: 4
217: 3
214: 2
197:
156:
151:
141:
138:
135:
132:
129:
126:
123:
120:
117:
115:
113:
105:
102:
99:
98:
96:
95:
55:
17:
12:
11:
5:
3104:
3094:
3093:
3088:
3083:
3069:
3068:
3063:Robert Feldt:
3061:
3035:
3028:
3014:
3005:
3004:External links
3002:
3001:
3000:
2995:
2982:
2977:
2957:
2952:
2930:
2927:
2924:
2923:
2895:
2864:
2835:
2820:
2811:Anne Broadbent
2798:
2780:(2): 227–234,
2764:
2745:
2726:
2711:
2692:
2672:
2650:
2609:
2588:
2587:
2585:
2582:
2581:
2580:
2575:
2570:
2565:
2560:
2553:
2550:
2537:
2534:
2498:
2497:
2494:
2493:
2490:
2487:(Door 2: Car)
2485:
2484:(Door 3: Car)
2480:
2475:
2470:
2467:
2463:
2462:
2457:
2452:
2447:
2442:
2439:
2436:
2432:
2431:
2428:
2425:
2422:
2419:
2416:
2413:
2403:
2402:
2398:
2374:
2373:
2358:
2355:
2337:
2334:
2329:
2324:
2321:
2316:
2313:
2310:
2307:
2304:
2301:
2298:
2295:
2292:
2289:
2286:
2283:
2280:
2277:
2274:
2269:
2266:
2259:
2254:
2251:
2248:
2245:
2241:
2237:
2234:
2231:
2228:
2224:
2220:
2215:
2212:
2205:
2200:
2197:
2194:
2191:
2187:
2183:
2180:
2176:
2172:
2169:
2166:
2163:
2160:
2157:
2154:
2151:
2148:
2144:
2138:
2135:
2130:
2127:
2123:
2117:
2114:
2107:
2102:
2099:
2096:
2093:
2089:
2085:
2082:
2079:
2076:
2072:
2068:
2065:
2062:
2059:
2056:
2053:
2050:
2047:
2044:
2041:
2038:
2035:
2011:
2008:
1991:
1988:
1974:
1967:
1964:
1961:
1956:
1953:
1950:
1947:
1944:
1938:
1934:
1930:
1910:
1891:
1888:
1882:
1879:
1871:Anne Broadbent
1851:
1848:
1846:
1843:
1753:
1750:
1740:
1737:
1729:
1728:
1717:
1714:
1711:
1708:
1705:
1702:
1699:
1696:
1693:
1690:
1687:
1684:
1681:
1678:
1675:
1672:
1669:
1666:
1663:
1658:
1654:
1650:
1645:
1642:
1638:
1634:
1631:
1628:
1623:
1620:
1617:
1613:
1598:
1597:
1586:
1583:
1580:
1577:
1574:
1571:
1568:
1563:
1559:
1555:
1550:
1547:
1544:
1540:
1517:
1514:
1511:
1491:
1477:
1476:
1465:
1462:
1459:
1456:
1453:
1450:
1447:
1444:
1441:
1436:
1432:
1428:
1425:
1422:
1419:
1416:
1413:
1410:
1407:
1402:
1399:
1395:
1391:
1388:
1385:
1382:
1379:
1374:
1370:
1366:
1361:
1358:
1354:
1350:
1347:
1344:
1321:
1301:
1298:
1278:
1275:
1258:
1236:
1232:
1220:
1219:
1208:
1205:
1202:
1199:
1194:
1190:
1186:
1181:
1177:
1173:
1170:
1167:
1164:
1160:
1154:
1151:
1146:
1143:
1140:
1135:
1132:
1126:
1122:
1119:
1116:
1112:
1106:
1102:
1099:
1093:
1090:
1087:
1082:
1078:
1075:
1068:
1061:
1058:
1054:
1049:
1046:
1034:thus given by
1020:
1019:
1008:
1003:
999:
996:
990:
987:
984:
981:
978:
975:
972:
969:
966:
963:
960:
957:
954:
951:
948:
942:
937:
934:
929:
903:
900:
897:
877:
874:
871:
868:
865:
862:
842:
822:
802:
799:
796:
793:
790:
787:
759:
754:
751:
746:
722:
719:
716:
689:
686:
672:
652:
641:
640:
629:
626:
623:
620:
617:
611:
605:
599:
593:
587:
581:
578:
564:
563:
552:
549:
543:
540:
537:
534:
528:
522:
519:
516:
513:
507:
501:
498:
484:cycle notation
459:
458:
449:
448:
440:
439:
438:
437:
436:
434:
431:
427:
426:
423:
422:
419:
416:
413:
410:
407:
404:
401:
398:
394:
393:
390:
387:
384:
381:
378:
375:
372:
369:
358:
357:
354:
353:
350:
347:
344:
341:
338:
335:
332:
329:
325:
324:
321:
318:
315:
312:
309:
306:
303:
300:
288:
287:
284:
280:
277:
274:
267:
266:
263:
262:
259:
256:
253:
250:
247:
244:
241:
238:
234:
233:
230:
227:
224:
221:
218:
215:
212:
211: 1
209:
196:
193:
185:
184:
181:
178:
175:
155:
152:
150:
147:
111:
93:
74:
73:
54:
51:
15:
9:
6:
4:
3:
2:
3103:
3092:
3089:
3087:
3084:
3082:
3079:
3078:
3076:
3066:
3062:
3059:
3055:
3049:
3045:
3039:
3038:MinutePhysics
3036:
3033:
3029:
3026:
3022:
3019:
3016:Oliver Nash:
3015:
3012:
3008:
3007:
2998:
2992:
2988:
2983:
2980:
2974:
2970:
2966:
2962:
2958:
2955:
2949:
2945:
2941:
2937:
2933:
2932:
2919:
2914:
2910:
2906:
2899:
2891:
2886:
2882:
2878:
2871:
2869:
2860:
2855:
2848:
2847:
2839:
2831:
2824:
2816:
2812:
2808:
2802:
2795:
2791:
2787:
2783:
2779:
2775:
2768:
2760:
2756:
2749:
2741:
2737:
2730:
2722:
2715:
2707:
2703:
2696:
2688:
2681:
2679:
2677:
2668:
2661:
2659:
2657:
2655:
2647:
2643:
2639:
2635:
2631:
2627:
2620:
2618:
2616:
2614:
2605:
2604:
2596:
2594:
2589:
2579:
2576:
2574:
2571:
2569:
2566:
2564:
2561:
2559:
2556:
2555:
2549:
2533:
2492:Door 2: Keys
2491:
2486:
2481:
2479:Door 1: Keys
2476:
2474:Door 3: Keys
2472:Door 2: Goat
2471:
2469:Door 2: Keys
2468:
2465:
2464:
2459:Door 1: Goat
2458:
2456:Door 3: Keys
2454:Door 1: Goat
2453:
2451:Door 2: Goat
2449:Door 1: Keys
2448:
2444:Door 1: Keys
2443:
2440:
2437:
2434:
2433:
2429:
2426:
2423:
2420:
2417:
2414:
2412:
2411:
2408:
2407:
2406:
2399:
2395:
2394:
2393:
2372:
2368:
2367:
2366:
2364:
2354:
2350:
2335:
2332:
2327:
2322:
2319:
2314:
2308:
2302:
2299:
2296:
2290:
2284:
2281:
2278:
2275:
2272:
2267:
2264:
2257:
2252:
2249:
2243:
2239:
2235:
2229:
2226:
2222:
2218:
2213:
2210:
2203:
2198:
2195:
2189:
2185:
2181:
2174:
2170:
2164:
2158:
2155:
2152:
2149:
2146:
2142:
2136:
2133:
2128:
2125:
2121:
2115:
2112:
2105:
2100:
2097:
2091:
2087:
2083:
2077:
2074:
2070:
2066:
2063:
2060:
2051:
2045:
2042:
2039:
2036:
2024:
2009:
2006:
1995:
1987:
1972:
1965:
1962:
1959:
1954:
1951:
1948:
1945:
1942:
1936:
1932:
1928:
1908:
1899:
1897:
1887:
1878:
1876:
1872:
1868:
1864:
1861:
1856:
1842:
1840:
1836:
1830:
1826:
1822:
1821:
1816:
1815:Peter Winkler
1812:
1811:
1806:
1805:locker puzzle
1801:
1798:
1794:
1790:
1786:
1782:
1777:
1775:
1771:
1767:
1763:
1759:
1749:
1747:
1736:
1734:
1715:
1712:
1709:
1706:
1703:
1700:
1697:
1694:
1691:
1688:
1685:
1682:
1679:
1676:
1673:
1670:
1667:
1664:
1656:
1652:
1648:
1643:
1640:
1636:
1632:
1629:
1615:
1603:
1602:
1601:
1584:
1581:
1575:
1572:
1569:
1566:
1561:
1557:
1542:
1530:
1529:
1528:
1509:
1489:
1482:
1463:
1460:
1457:
1454:
1448:
1445:
1442:
1439:
1434:
1430:
1423:
1417:
1414:
1411:
1408:
1405:
1400:
1397:
1393:
1386:
1383:
1380:
1372:
1368:
1364:
1359:
1356:
1352:
1345:
1342:
1335:
1334:
1333:
1319:
1299:
1296:
1283:
1274:
1272:
1256:
1234:
1230:
1206:
1203:
1200:
1192:
1188:
1184:
1179:
1175:
1168:
1165:
1162:
1158:
1152:
1149:
1144:
1141:
1138:
1133:
1130:
1124:
1120:
1117:
1114:
1110:
1104:
1100:
1097:
1091:
1088:
1085:
1080:
1076:
1073:
1066:
1059:
1056:
1052:
1047:
1044:
1037:
1036:
1035:
1033:
1029:
1028:single events
1025:
1006:
1001:
997:
994:
988:
985:
979:
976:
973:
967:
964:
958:
955:
952:
946:
935:
932:
917:
916:
915:
901:
898:
895:
875:
869:
866:
863:
840:
820:
800:
794:
791:
788:
777:
752:
749:
720:
717:
714:
705:
703:
694:
685:
670:
650:
624:
615:
609:
603:
597:
591:
585:
579:
569:
568:
567:
547:
541:
532:
526:
520:
511:
505:
499:
489:
488:
487:
485:
481:
477:
473:
469:
453:
444:
430:
420:
417:
414:
411:
408:
405:
402:
399:
396:
395:
391:
388:
385:
382:
379:
376:
373:
370:
367:
366:
363:
362:
361:
351:
348:
345:
342:
339:
336:
333:
330:
327:
326:
322:
319:
316:
313:
310:
307:
304:
301:
298:
297:
294:
293:
292:
285:
281:
278:
275:
272:
271:
270:
260:
257:
254:
251:
248:
245:
242:
239:
236:
235:
231:
228:
225:
222:
219:
216:
213:
210:
207:
206:
203:
202:
201:
192:
190:
182:
179:
176:
173:
172:
171:
168:
166:
162:
146:
91:
87:
83:
79:
78:independently
72:
68:
67:
66:
64:
60:
50:
47:
45:
44:combinatorics
41:
37:
34:
30:
21:
3091:Permutations
3009:Rob Heaton:
2986:
2971:, Springer,
2964:
2943:
2908:
2904:
2898:
2880:
2876:
2845:
2838:
2829:
2823:
2814:
2801:
2777:
2773:
2767:
2758:
2754:
2748:
2739:
2729:
2720:
2714:
2706:The Emissary
2705:
2695:
2686:
2666:
2629:
2625:
2602:
2539:
2499:
2477:Door 2: Car
2461:Door 3: Car
2446:Door 2: Car
2441:Door 1: Car
2438:Door 1: Car
2404:
2375:
2369:
2360:
2351:
2025:
1996:
1993:
1900:
1895:
1893:
1884:
1865:
1860:Michael Saks
1857:
1853:
1818:
1808:
1804:
1802:
1785:The Emissary
1784:
1778:
1761:
1755:
1742:
1730:
1599:
1478:
1288:
1221:
1021:
914:is equal to
706:
699:
642:
565:
465:
428:
359:
289:
268:
198:
186:
169:
157:
75:
69:
56:
48:
33:mathematical
28:
26:
1850:Empty boxes
1758:proceedings
1277:Asymptotics
776:combination
468:permutation
165:independent
161:information
86:probability
3075:Categories
2929:Literature
2859:2407.07190
2850:(Preprint)
2807:David Avis
2584:References
1867:David Avis
1831:in a 2023
1829:Veritasium
1739:Optimality
2852:, arXiv,
2646:123089718
2632:: 28–31,
2466:Player 2
2435:Player 1
2315:−
2303:
2285:
2279:−
2247:⌋
2233:⌊
2223:∑
2219:−
2193:⌋
2179:⌊
2175:∑
2159:
2153:−
2129:−
2095:⌋
2081:⌊
2071:∑
2061:⋅
2046:
2040:−
1963:
1952:
1946:
1744:based on
1713:≈
1707:
1701:−
1689:
1683:−
1680:γ
1674:γ
1671:−
1633:−
1622:∞
1619:→
1585:γ
1573:
1567:−
1549:∞
1546:→
1516:∞
1513:→
1490:γ
1479:With the
1461:
1455:−
1446:
1440:−
1412:
1406:−
1387:−
1365:−
1346:−
1201:≈
1185:−
1169:−
1142:…
1121:−
1089:…
1048:−
977:−
968:⋅
956:−
947:⋅
867:−
792:−
3021:Archived
2963:(2013),
2942:(2009),
2911:(2): 1,
2883:(2): 1,
2552:See also
1845:Variants
1716:0.30685.
480:disjoint
195:Examples
154:Strategy
149:Solution
82:randomly
3058:YouTube
3048:YouTube
2530:
2518:
2514:
2502:
2390:
2378:
1839:YouTube
1817:in the
1813:and by
1787:of the
1760:of the
1752:History
1249:is the
1204:0.31183
283:drawer.
109:
97:
90:product
53:Problem
36:problem
2993:
2975:
2950:
2792:
2644:
1797:signed
1502:, for
1222:where
613:
607:
601:
595:
589:
583:
545:
530:
524:
509:
503:
84:, the
2854:arXiv
2794:90893
2790:S2CID
2642:S2CID
2546:(1/2)
1834:video
1770:below
1766:ICALP
476:cycle
189:below
116:0.000
31:is a
3050:and
2991:ISBN
2973:ISBN
2948:ISBN
1869:and
1793:ROMs
1269:-th
899:>
718:>
142:0008
80:and
61:and
42:and
27:The
3056:on
3046:on
2913:doi
2885:doi
2782:doi
2634:doi
1960:log
1949:log
1943:log
1837:on
1612:lim
1539:lim
1289:If
1180:100
1153:100
1105:100
1098:100
1074:100
1057:100
995:100
974:100
933:100
864:100
750:100
486:as
139:000
136:000
133:000
130:000
127:000
124:000
121:000
118:000
38:in
3077::
3040::
2967:,
2938:,
2909:32
2907:,
2881:31
2879:,
2867:^
2809:,
2788:,
2778:27
2776:,
2759:37
2757:,
2738:,
2704:,
2675:^
2653:^
2640:,
2630:28
2628:,
2612:^
2592:^
2401:1.
2397:3.
2365::
2300:ln
2282:ln
2156:ln
2043:ln
1841:.
1704:ln
1686:ln
1570:ln
1464:2.
1458:ln
1443:ln
1409:ln
1193:50
1134:51
1081:51
902:50
721:50
421:2
352:1
261:2
114:≈
65::
2915::
2887::
2856::
2784::
2636::
2527:3
2524:/
2521:2
2511:3
2508:/
2505:2
2387:9
2384:/
2381:4
2336:2
2333:1
2328:=
2323:2
2320:1
2312:)
2309:2
2306:(
2297:+
2294:)
2291:2
2288:(
2276:1
2273:=
2268:n
2265:1
2258:N
2253:1
2250:+
2244:2
2240:/
2236:n
2230:=
2227:k
2214:k
2211:1
2204:N
2199:1
2196:+
2190:2
2186:/
2182:n
2171:+
2168:)
2165:2
2162:(
2150:1
2147:=
2143:)
2137:n
2134:k
2126:1
2122:(
2116:k
2113:1
2106:N
2101:1
2098:+
2092:2
2088:/
2084:n
2078:=
2075:k
2067:+
2064:1
2058:)
2055:)
2052:2
2049:(
2037:1
2034:(
2010:2
2007:1
1973:)
1966:N
1955:N
1937:N
1933:(
1929:O
1909:N
1764:(
1710:2
1698:1
1695:=
1692:2
1677:+
1668:1
1665:=
1662:)
1657:n
1653:H
1649:+
1644:n
1641:2
1637:H
1630:1
1627:(
1616:n
1582:=
1579:)
1576:n
1562:n
1558:H
1554:(
1543:n
1510:n
1452:)
1449:n
1435:n
1431:H
1427:(
1424:+
1421:)
1418:n
1415:2
1401:n
1398:2
1394:H
1390:(
1384:1
1381:=
1378:)
1373:n
1369:H
1360:n
1357:2
1353:H
1349:(
1343:1
1320:n
1300:n
1297:2
1257:n
1235:n
1231:H
1207:,
1198:)
1189:H
1176:H
1172:(
1166:1
1163:=
1159:)
1150:1
1145:+
1139:+
1131:1
1125:(
1118:1
1115:=
1111:)
1101:!
1092:+
1086:+
1077:!
1067:(
1060:!
1053:1
1045:1
1007:.
1002:l
998:!
989:=
986:!
983:)
980:l
971:(
965:!
962:)
959:1
953:l
950:(
941:)
936:l
928:(
896:l
876:!
873:)
870:l
861:(
841:l
821:l
801:!
798:)
795:1
789:l
786:(
758:)
753:l
745:(
715:l
671:l
651:l
628:)
625:6
622:(
619:)
616:2
610:8
604:5
598:4
592:7
586:3
580:1
577:(
551:)
548:6
542:3
539:(
536:)
533:8
527:4
521:2
518:(
515:)
512:5
506:7
500:1
497:(
418:4
415:6
412:8
409:5
406:7
403:1
400:3
349:5
346:3
343:2
340:8
337:6
334:4
331:7
258:5
255:3
252:1
249:8
246:6
243:4
240:7
112:)
106:2
103:/
100:1
94:(
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.