298:
358:, the algorithms may give different results for points in the regions where the polygon intersects itself, where the polygon does not have a clearly defined inside and outside. One solution using the even-odd rule is to transform (complex) polygons into simpler ones that are even-odd-equivalent before the intersection check. This, however, is computationally expensive. It is less expensive to use the fast non-zero winding number algorithm, which gives the correct result even when the polygon overlaps itself.
310:
cast from the point being checked. Whenever that ray crosses an edge of the polygon, Juan Pineda's edge crossing algorithm (1988) is used to determine how the crossing will affect the winding number. As Sunday describes it, if the edge crosses the ray going "upwards", the winding number is incremented; if it crosses the ray "downwards", the number is decremented. Sunday's algorithm gives the correct answer for nonsimple polygons, whereas the boundary crossing algorithm fails in this case.
387:
96:
200:: for two sides adjacent to the same vertex the straightforward computation of the intersection with a ray may not give the vertex in both cases. If the polygon is specified by its vertices, then this problem is eliminated by checking the y-coordinates of the ray and the ends of the tested polygon side before actual computation of the intersection. In other cases, when polygon sides are computed from other types of data, other tricks must be applied for the
134:, and was known as early as 1962. The algorithm is based on a simple observation that if a point moves along a ray from infinity to the probe point and if it crosses the boundary of a polygon, possibly several times, then it alternately goes from the outside to inside, then from the inside to the outside, etc. As a result, after every two "border crossings" the moving point goes outside. This observation may be mathematically proved using the
20:
185:
similar problem arises with horizontal segments that happen to fall on the ray. The issue is solved as follows: If the intersection point is a vertex of a tested polygon side, then the intersection counts only if the other vertex of the side lies below the ray. This is effectively equivalent to considering vertices
184:
of a polygon, then it will intersect 2 segments at their endpoints. While it is OK for the case of the topmost vertex in the example or the vertex between crossing 4 and 5, the case of the rightmost vertex (in the example) requires that we count one intersection for the algorithm to work correctly. A
309:
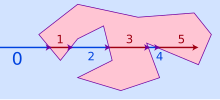
An improved algorithm to calculate the winding number was developed by Dan Sunday in 2001. It does not use angles in calculations, nor any trigonometry, and functions exactly the same as the ray casting algorithms described above. Sunday's algorithm works by considering an infinite horizontal ray
150:, the results may be incorrect if the point lies very close to that boundary, because of rounding errors. For some applications, like video games or other entertainment products, this is not a large concern since they often favor speed over precision. However, for a
248:, which generally makes this algorithm performance-inefficient (slower) compared to the ray casting algorithm. Luckily, these inverse trigonometric functions do not need to be computed. Since the result, the sum of all angles, can add up to 0 or
99:
The number of intersections for a ray passing from the exterior of the polygon to any point: If odd, it shows that the point lies inside the polygon; if even, the point lies outside the polygon. This test also works in three
179:
Most implementations of the ray casting algorithm consecutively check intersections of a ray with all sides of the polygon in turn. In this case the following problem must be addressed. If the ray passes exactly through a
294:) only, it is sufficient to track through which quadrants the polygon winds, as it turns around the test point, which makes the winding number algorithm comparable in speed to counting the boundary crossings.
327:
for defining a way of filling with color various shapes (such as path, polyline, polygon, text etc.). The algorithm of filling is influenced by 'fill-rule' attribute. The value may be either
112:, starting from the point and going in any fixed direction, intersects the edges of the polygon. If the point is on the outside of the polygon the ray will intersect its edge an
236:
A point is inside the polygon if either count of intersections is odd or point lies on an edge of the polygon. If none of the conditions are true, then point lies outside.
292:
269:
370:
setting: given a single polygon and a sequence of query points, quickly find the answers for each query point. Clearly, any of the general approaches for planar
494:
216:
with respect to the polygon. If the winding number is non-zero, the point lies inside the polygon. This algorithm is sometimes also known as the
77:
An attempt of computer graphics veterans to trace the history of the problem and some tricks for its solution can be found in an issue of the
485:
724:
723:. Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (
305:
algorithm. A winding number of 0 means the point is outside the polygon; other values indicate the point is inside the polygon
614:
595:
526:
120:
of times. The status of a point on the edge of the polygon depends on the details of the ray intersection algorithm.
695:
671:
245:
737:
784:
437:
56:
197:
147:
633:
398:
789:
509:
324:
482:
161:
584:
Weiler, Kevin (1994), "An
Incremental Angle Point in Polygon Test", in Heckbert, Paul S. (ed.),
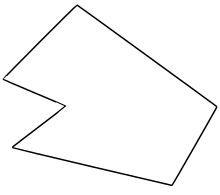
39:) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a
212:
Another technique used to check if a point is inside a polygon is to compute the given point's
28:
721:
A Simple and
Correct Even-Odd Algorithm for the Point-in-Polygon Problem for Complex Polygons
469:
64:
47:
problems and finds applications in areas that deal with processing geometrical data, such as
274:
251:
201:
135:
90:
116:
of times. If the point is on the inside of the polygon then it will intersect the edge an
8:
585:
441:
422:
151:
196:
Once again, the case of the ray passing through a vertex may pose numerical problems in
757:
158:
569:
552:
70:
An early description of the problem in computer graphics shows two common approaches (
794:
591:
181:
128:
109:
48:
763:
564:
418:
355:
297:
154:
489:
464:
367:
351:
241:
60:
52:
769:
618:
514:
426:
371:
302:
213:
105:
44:
778:
230:
Draw a horizontal line to the right of each point and extend it to infinity.
507:
Shimrat, M., "Algorithm 112: Position of point relative to polygon" 1962,
218:
590:, San Diego, CA, USA: Academic Press Professional, Inc., pp. 16–23,
445:
113:
71:
386:
374:
may be used. Simpler solutions are available for some special polygons.
366:
The point in polygon problem may be considered in the general repeated
117:
95:
696:"Painting: Filling, Stroking, Colors and Paint Servers – SVG Tiny 1.2"
672:"Painting: Filling, Stroking, Colors and Paint Servers – SVG Tiny 1.2"
336:
467:
et al.,"A Characterization of Ten Hidden-Surface
Algorithms" 1974,
642:
430:
104:
One simple way of finding whether the point is inside or outside a
448:. The dot product method extends naturally to any convex polygon.
718:
650:
527:"How to check if a given point lies inside or outside a polygon?"
233:
Count the number of times the line intersects with polygon edges.
40:
19:
172:(the Line), in which case the algorithm should stop and report "
16:
Determining where a point is in relation to a coplanar polygon
226:
To check if a given point lies inside or outside a polygon:
244:
by each side of the polygon. However, this involves costly
354:, the algorithms will give the same result. However, for
240:
One way to compute the winding number is to sum up the
339:, there is a central "hole" (visible background) with
553:"The point in polygon problem for arbitrary polygons"
277:
254:
436:The triangle case can be solved easily by use of a
286:
263:
776:
764:http://www.ics.uci.edu/~eppstein/161/960307.html
768:Winding number versus crossing number methods:
635:A Parallel Algorithm for Polygon Rasterization
550:
123:This algorithm is sometimes also known as the
74:and angle summation) in use as early as 1974.
770:http://geomalgorithms.com/a03-_inclusion.html
515:https://dl.acm.org/doi/10.1145/368637.368653
361:
207:
719:Michael Galetzka, Patrick Glauner (2017).
568:
608:
606:
296:
94:
84:
18:
777:
742:...the most famous methods to solve it
631:
612:
583:
544:
603:
483:"Point in Polygon, One More Time..."
417:Simpler algorithms are possible for
381:
141:
615:"Inclusion of a Point in a Polygon"
13:
313:
176:lies very close to the boundary."
146:If implemented on a computer with
14:
806:
551:Hormann, K.; Agathos, A. (2001).
498:, vol. 3 no. 4, October 1, 1990.
385:
377:
157:, one would have to introduce a
738:Accurate point in triangle test
731:
712:
688:
344:
340:
332:
328:
246:inverse trigonometric functions
664:
625:
577:
519:
501:
476:
458:
301:Visualization of Dan Sunday's
57:geographic information systems
23:An example of a simple polygon
1:
570:10.1016/S0925-7721(01)00012-8
513:Volume 5 Issue 8, Aug. 1962.
451:
438:barycentric coordinate system
168:(the point) lies within ε of
649:. Vol. 22, no. 4.
632:Pineda, Juan (August 1988).
323:Similar methods are used in
198:finite precision arithmetics
148:finite precision arithmetics
108:is to test how many times a
7:
751:
164:ε and test in line whether
10:
811:
189:the ray as lying slightly
88:
43:. It is a special case of
758:Java Topology Suite (JTS)
510:Communications of the ACM
125:crossing number algorithm
362:Point in polygon queries
208:Winding number algorithm
727:2017), Volume 1: GRAPP.
557:Computational Geometry
318:
306:
288:
265:
101:
29:computational geometry
24:
470:ACM Computing Surveys
300:
289:
287:{\displaystyle 2\pi }
266:
264:{\displaystyle 2\pi }
98:
85:Ray casting algorithm
65:computer-aided design
22:
785:Geometric algorithms
613:Sunday, Dan (2001).
423:star-shaped polygons
335:. For example, in a
275:
252:
202:numerical robustness
136:Jordan curve theorem
91:Jordan curve theorem
621:on 26 January 2013.
442:parametric equation
488:2018-05-24 at the
397:. You can help by
307:
284:
261:
204:of the algorithm.
102:
25:
647:Computer Graphics
419:monotone polygons
415:
414:
271:(or multiples of
142:Limited precision
49:computer graphics
802:
790:Point (geometry)
745:
735:
729:
728:
716:
710:
709:
707:
706:
692:
686:
685:
683:
682:
668:
662:
661:
659:
657:
640:
629:
623:
622:
617:. Archived from
610:
601:
600:
587:Graphics Gems IV
581:
575:
574:
572:
548:
542:
541:
539:
538:
523:
517:
505:
499:
495:Ray Tracing News
480:
474:
462:
410:
407:
389:
382:
356:complex polygons
346:
343:, and none with
342:
334:
330:
293:
291:
290:
285:
270:
268:
267:
262:
242:angles subtended
155:computer program
152:formally correct
79:Ray Tracing News
33:point-in-polygon
810:
809:
805:
804:
803:
801:
800:
799:
775:
774:
754:
749:
748:
736:
732:
717:
713:
704:
702:
694:
693:
689:
680:
678:
670:
669:
665:
655:
653:
638:
630:
626:
611:
604:
598:
582:
578:
549:
545:
536:
534:
525:
524:
520:
506:
502:
490:Wayback Machine
481:
477:
465:Ivan Sutherland
463:
459:
454:
427:convex polygons
411:
405:
402:
395:needs expansion
380:
368:geometric query
364:
352:simple polygons
321:
316:
314:Implementations
276:
273:
272:
253:
250:
249:
210:
144:
93:
87:
61:motion planning
53:computer vision
17:
12:
11:
5:
808:
798:
797:
792:
787:
773:
772:
766:
760:
753:
750:
747:
746:
730:
711:
687:
663:
624:
602:
596:
576:
543:
518:
500:
475:
456:
455:
453:
450:
413:
412:
392:
390:
379:
376:
372:point location
363:
360:
320:
317:
315:
312:
303:winding number
283:
280:
260:
257:
238:
237:
234:
231:
214:winding number
209:
206:
143:
140:
106:simple polygon
86:
83:
45:point location
15:
9:
6:
4:
3:
2:
807:
796:
793:
791:
788:
786:
783:
782:
780:
771:
767:
765:
761:
759:
756:
755:
743:
739:
734:
726:
722:
715:
701:
697:
691:
677:
673:
667:
652:
648:
644:
637:
636:
628:
620:
616:
609:
607:
599:
597:0-12-336155-9
593:
589:
588:
580:
571:
566:
562:
558:
554:
547:
532:
531:GeeksforGeeks
528:
522:
516:
512:
511:
504:
497:
496:
491:
487:
484:
479:
473:vol. 6 no. 1.
472:
471:
466:
461:
457:
449:
447:
443:
439:
434:
432:
428:
424:
420:
409:
400:
396:
393:This section
391:
388:
384:
383:
378:Special cases
375:
373:
369:
359:
357:
353:
348:
338:
326:
311:
304:
299:
295:
281:
278:
258:
255:
247:
243:
235:
232:
229:
228:
227:
224:
222:
220:
215:
205:
203:
199:
194:
192:
188:
183:
177:
175:
171:
167:
163:
160:
156:
153:
149:
139:
137:
133:
130:
129:even–odd rule
126:
121:
119:
115:
111:
107:
97:
92:
82:
80:
75:
73:
68:
66:
62:
58:
54:
50:
46:
42:
38:
34:
30:
21:
762:Discussion:
741:
733:
720:
714:
703:. Retrieved
699:
690:
679:. Retrieved
675:
666:
654:. Retrieved
646:
634:
627:
619:the original
586:
579:
560:
556:
546:
535:. Retrieved
533:. 2013-07-11
530:
521:
508:
503:
493:
478:
468:
460:
435:
416:
403:
399:adding to it
394:
365:
349:
322:
308:
239:
225:
219:nonzero-rule
217:
211:
195:
190:
186:
178:
173:
169:
165:
145:
131:
124:
122:
103:
78:
76:
69:
36:
32:
26:
446:dot product
406:August 2013
347:attribute.
114:even number
100:dimensions.
72:ray casting
779:Categories
705:2021-07-24
700:www.w3.org
681:2021-07-24
676:www.w3.org
563:(3): 131.
537:2024-08-23
452:References
118:odd number
89:See also:
725:VISIGRAPP
431:triangles
337:pentagram
282:π
259:π
221:algorithm
193:the ray.
162:tolerance
159:numerical
132:algorithm
795:Polygons
752:See also
656:8 August
643:SIGGRAPH
486:Archived
651:Atlanta
345:nonzero
341:evenodd
333:evenodd
329:nonzero
127:or the
67:(CAD).
59:(GIS),
41:polygon
594:
182:vertex
63:, and
31:, the
645:'88.
639:(PDF)
191:above
658:2021
592:ISBN
429:and
350:For
565:doi
492:,
444:or
401:.
331:or
325:SVG
319:SVG
110:ray
37:PIP
27:In
781::
698:.
674:.
641:.
605:^
561:20
559:.
555:.
529:.
440:,
433:.
425:,
421:,
223:.
187:on
138:.
81:.
55:,
51:,
744:"
740:"
708:.
684:.
660:.
573:.
567::
540:.
408:)
404:(
279:2
256:2
174:P
170:L
166:P
35:(
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.