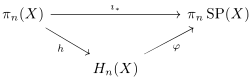1631:
183:
782:
2256:
is that it is of particular interest for algebraic geometry since it allows one to reformulate homology only using homotopy. Since applying methods from algebraic topology can be quite insightful in this field, one tries to transfer these to algebraic geometry. This could be achieved for homotopy
566:
2117:
1146:
777:{\displaystyle \qquad \dots \xrightarrow {\partial } {\tilde {h}}_{n}(A)\xrightarrow {i_{*}} {\tilde {h}}_{n}(X)\xrightarrow {q_{*}} {\tilde {h}}_{n}(X/A)\xrightarrow {\partial } {\tilde {h}}_{n-1}(A)\xrightarrow {i_{*}} \dots }
2020:
70:, one can see that the latter actually defines a homology theory. Nevertheless, none of these allow one to directly reduce homology to homotopy. This advantage of the Dold-Thom theorem makes it particularly interesting for
962:
2031:
904:
1930:
1033:
1176:
1038:
1603:
One should bear in mind that there is a variety of different proofs although this one is seemingly the most popular. For example, proofs have been established via
1659:. All sides except possibly the one at the bottom commute in this diagram. Therefore, one sees that the whole diagram commutes when considering where 1 ∈ π
1945:
1673:
gets mapped to. However, by using the suspension isomorphisms for homotopy respectively homology groups, the task reduces to showing the assertion for
909:
2112:{\displaystyle \operatorname {SP} \left(\bigvee _{\alpha }X_{\alpha }\right)\cong \prod _{\alpha }\operatorname {SP} (X_{\alpha }),}
1776:
and that it therefore has the weak homotopy type of a generalised
Eilenberg-MacLane space. The theorem amounts to saying that all
2584:
2565:
2487:
2456:
2352:
863:
1321:) consisting of connected complexes. First of all, as every CW complex is homotopy equivalent to a simplicial complex,
1271:. So it only remains to verify the axioms 2 and 4. The crux of this undertaking will be the first point. This is where
1263:
is a functor fulfilling property 1 as SP is a homotopy functor. Moreover, the third property is clear since one has SP(
1619:
In order to verify the compatibility with the
Hurewicz homomorphism, it suffices to show that the statement holds for
2505:
1852:
47:
with the infinite symmetric product defines a reduced homology theory. One of the main tools used in doing so are
1877:
1611:. One can also proof the theorem using other notions of a homology theory (the Eilenberg-Steenrod axioms e.g.).
997:
67:
1742:
Another application is a new proof of a theorem first stated by Moore. It basically predicates the following:
43:
groups. The most common version of its proof consists of showing that the composition of the homotopy group
2253:
32:
1702:. One gets the result by first forming the homotopy pushout square of the inclusions of the intersection
52:
2448:
58:
There are several other theorems constituting relations between homotopy and homology, for example the
2547:
1757:
1594:
414:
1349:. This will not change anything as SP is a homotopy functor. It suffices to prove by induction that
1141:{\displaystyle \qquad i_{*}\colon \varinjlim {\tilde {h}}_{n}(X_{\lambda })\to {\tilde {h}}_{n}(X),}
2327:
1151:
1462:
restricted to each of the preimages of these three sets is a quasifibration. It can be shown that
1761:
1699:
1604:
63:
1780:-invariants of a path-connected, commutative and associative H-space with strict unit vanish.
1458:
and shows that these two sets are, together with their intersection, distinguished, i.e. that
2517:
2394:
2248:
What distinguishes the Dold-Thom theorem from other alternative foundations of homology like
150:
1503:
is not even a fibration. However, that turns out not to be the case: Take an arbitrary path
2431:
2392:
Dold, Albrecht; Thom, René (1958), "Quasifaserungen und unendliche symmetrische
Produkte",
2025:
given by summing up the images of the coordinates. But as there are natural homeomorphisms
1330:
510:
1600:
Verifying the fourth axiom can be done quite elementary, in contrast to the previous one.
8:
2261:. So the Dold-Thom theorem yields a foundation of homology having an algebraic analogue.
2258:
1935:
if one takes the maps to be basepoint-preserving. Then the special H-space structure of
2530:
2419:
2381:
71:
20:
2442:
2501:
2483:
2452:
2411:
2385:
2348:
2257:
theory, but for homology theory only in a rather limited way using a formulation via
2522:
2515:
Spanier, Edwin (1959), "Infinite
Symmetric Products, Function Spaces and Duality",
2475:
2403:
2371:
2015:{\displaystyle f\colon \operatorname {SP} \left(\bigvee _{n}M(G_{n},n)\right)\to X}
1338:
242:
59:
40:
2303:
16:
On the homotopy groups of the infinite symmetric product of a connected CW complex
2427:
2249:
1482:) and the long exact sequence of such a one implies that axiom 2 is satisfied as
402:
28:
2171:) is the Hurewicz homomorphism and as H-spaces have abelian fundamental groups,
2362:
Bandklayder, Lauren (2019), "The Dold-Thom
Theorem via Factoriation Homology",
1608:
1272:
440:
48:
2376:
2578:
2569:
2438:
2415:
857:
406:
321:
439:
from the category of basepointed, connected CW complexes to the category of
2560:
2551:
1698:
One direct consequence of the Dold-Thom theorem is a new way to derive the
410:
122:
denotes reduced homology and SP stands for the infinite symmetric product.
2236:)) into the cartesian product is a weak homotopy equivalence. Therefore,
1630:
2534:
2479:
2423:
1420:= 0 this is trivially fulfilled. In the induction step, one decomposes
182:
51:. The theorem has been generalised in various ways, for example by the
36:
2240:
has the weak homotopy type of a generalised
Eilenberg-MacLane space.
2213:). This also implies that the natural inclusion of the weak product Π
245:. The common point of the two copies is supposed to be the point 0 ∈
238:
2526:
2407:
758:
714:
661:
616:
578:
2556:
957:{\displaystyle i_{\lambda }^{\mu }\colon X_{\lambda }\to X_{\mu }}
126:
It is also very useful that there exists an isomorphism φ : π
1750:
44:
2466:
May, J. Peter (1990), "Weak
Equivalences and Quasifibrations",
1614:
1730:
themselves. Then one applies SP to that square and finally π
2307:
413:
chose in their initial proof a slight modification of the
215:
The following example illustrates that the requirement of
2343:
Aguilar, Marcelo; Gitler, Samuel; Prieto, Carlos (2008).
845:) be the system of compact subspaces of a pointed space
2034:
1948:
1880:
1154:
1041:
1000:
912:
866:
569:
899:{\displaystyle i_{\lambda }\colon X_{\lambda }\to X}
2342:
1772:) has this property for every connected CW complex
2111:
2014:
1924:
1170:
1140:
1027:
956:
898:
776:
516:There are natural boundary homomorphisms ∂ :
219:being a CW complex cannot be dropped offhand: Let
1471:is then already distinguished itself. Therefore,
1184:One can show that for a reduced homology theory (
2576:
994:) is a direct system as well with the morphisms
2345:Algebraic Topology from a Homotopical Viewpoint
320:) defined by φ(, ) = () is a homeomorphism for
2557:The Dold-Thom theorem for infinity categories?
1749:A path-connected, commutative and associative
386:One wants to show that the family of functors
179:), meaning that one has a commutative diagram
1593:, hence different from the basepoint, so the
563:being connected, yielding an exact sequence
1615:Compatibility with the Hurewicz homomorphism
2566:Group structure on Eilenberg-MacLane spaces
2361:
2179:. Thanks to the Dold-Thom theorem, each SP(
1925:{\displaystyle \bigvee _{n}M(G_{n},n)\to X}
1478:is indeed a quasifibration on the whole SP(
1693:
2495:
2375:
2347:. Springer Science & Business Media.
1028:{\displaystyle {i_{\lambda }^{\mu }}_{*}}
2391:
1627:. This is because one then gets a prism
860:together with the inclusions. Denote by
2514:
2437:
2364:Journal of Homotopy and Related Sources
1756:with a strict identity element has the
417:, namely calling a family of functors (
249:meeting every circle. On the one hand,
2577:
381:
2243:
2196:)) is now an Eilenberg-MacLane space
1737:
1677:. But in this case the inclusion SP(
1548:). Then any lift of this path to SP(
196:is the map induced by the inclusion
2465:
1581:. But this means that its endpoint
1313:is a quasifibration for a CW pair (
241:of two copies of the cone over the
13:
2276:Dold and Thom (1958), Example 6.11
2122:with Π denoting the weak product,
1734:to the resulting pullback square.
1629:
1278:The goal is to prove that the map
715:
579:
274:) is trivial. On the other hand, π
181:
14:
2596:
2541:
1178:is required to be an isomorphism.
2470:, Lecture Notes in Mathematics,
849:containing the basepoint. Then (
1688:
1206:there is a natural isomorphism
1042:
570:
149:) which is compatible with the
62:. Another approach is given by
2585:Theorems in algebraic topology
2330:An essay by Thomas Barnet-Lamb
2321:
2312:
2297:
2288:
2285:Dold and Thom (1958), Satz 6.8
2279:
2270:
2175:also induces isomorphisms on π
2103:
2090:
2006:
1998:
1979:
1916:
1913:
1894:
1532:and interpret it as a path in
1429:into an open neighbourhood of
1297:) induced by the quotient map
1132:
1126:
1114:
1104:
1101:
1088:
1076:
941:
890:
751:
745:
727:
707:
693:
681:
654:
648:
636:
609:
603:
591:
334:But this implies that either π
77:
68:Freudenthal suspension theorem
1:
2336:
1685:) is a homotopy equivalence.
1171:{\displaystyle i_{\lambda *}}
260:) is an infinite group while
2496:Piccinini, Renzo A. (1992).
2294:Hatcher (2002), Theorem 2C.5
2254:Alexander-Spanier cohomology
1828:inducing an isomorphism on π
7:
2498:Lectures on Homotopy Theory
2163:) induced by the inclusion
509:), where ≃ denotes pointed
304:)) holds since φ : SP(
86:For a connected CW complex
53:Almgren isomorphism theorem
10:
2601:
2548:Why the Dold-Thom theorem?
2449:Cambridge University Press
2318:Hatcher (2002), Lemma 4.31
1838:≥ 2 and an isomorphism on
2377:10.1007/s40062-018-0219-1
2126:induces isomorphisms on π
1807:). Then there exist maps
1595:Homotopy lifting property
1374:is a quasifibration with
1035:. Then the homomorphism
415:Eilenberg-Steenrod axioms
2264:
1783:
1337:will be replaced by the
1762:Eilenberg-MacLane space
1700:Mayer-Vietoris sequence
1694:Mayer-Vietoris sequence
1647:) represented by a map
1597:fails to be fulfilled.
1496:One may wonder whether
445:reduced homology theory
2468:Springer Lecture Notes
2113:
2016:
1926:
1634:
1605:factorisation homology
1172:
1142:
1029:
958:
900:
778:
186:
64:stable homotopy theory
2518:Annals of Mathematics
2395:Annals of Mathematics
2328:The Dold-Thom theorem
2304:The Dold-Thom theorem
2114:
2017:
1927:
1637:for each Element ∈ π
1633:
1329:can be assumed to be
1173:
1143:
1030:
959:
901:
796:is the inclusion and
779:
185:
151:Hurewicz homomorphism
2032:
1946:
1878:
1871:). These give a map
1331:simplicial complexes
1152:
1039:
998:
910:
864:
812:is the quotient map.
567:
511:homotopy equivalence
39:are the same as its
1017:
927:
835:denotes the circle.
769:
718:
672:
627:
582:
382:Sketch of the proof
2480:10.1007/BFb0083834
2444:Algebraic Topology
2244:Algebraic geometry
2109:
2083:
2055:
2012:
1975:
1922:
1890:
1758:weak homotopy type
1738:A theorem of Moore
1635:
1168:
1138:
1064:
1025:
1003:
954:
913:
896:
774:
187:
84:Dold-Thom theorem.
72:algebraic geometry
21:algebraic topology
2489:978-3-540-52658-2
2458:978-0-521-79540-1
2398:, Second Series,
2354:978-0-387-22489-3
2074:
2046:
1966:
1881:
1760:of a generalised
1710:of two subspaces
1589:is a multiple of
1552:) is of the form
1524:approaching some
1341:of the inclusion
1117:
1079:
1057:
964:the inclusion if
770:
730:
719:
684:
673:
639:
628:
594:
583:
547:) for each pair (
378:) does not hold.
33:symmetric product
25:Dold-Thom theorem
2592:
2537:
2511:
2492:
2462:
2434:
2388:
2379:
2358:
2331:
2325:
2319:
2316:
2310:
2301:
2295:
2292:
2286:
2283:
2277:
2274:
2118:
2116:
2115:
2110:
2102:
2101:
2082:
2070:
2066:
2065:
2064:
2054:
2021:
2019:
2018:
2013:
2005:
2001:
1991:
1990:
1974:
1931:
1929:
1928:
1923:
1906:
1905:
1889:
1339:mapping cylinder
1275:come into play:
1177:
1175:
1174:
1169:
1167:
1166:
1147:
1145:
1144:
1139:
1125:
1124:
1119:
1118:
1110:
1100:
1099:
1087:
1086:
1081:
1080:
1072:
1065:
1052:
1051:
1034:
1032:
1031:
1026:
1024:
1023:
1018:
1016:
1011:
963:
961:
960:
955:
953:
952:
940:
939:
926:
921:
905:
903:
902:
897:
889:
888:
876:
875:
783:
781:
780:
775:
768:
767:
754:
744:
743:
732:
731:
723:
710:
703:
692:
691:
686:
685:
677:
671:
670:
657:
647:
646:
641:
640:
632:
626:
625:
612:
602:
601:
596:
595:
587:
574:
447:if they satisfy
243:Hawaiian earring
66:. Thanks to the
60:Hurewicz theorem
41:reduced homology
31:of the infinite
27:states that the
2600:
2599:
2595:
2594:
2593:
2591:
2590:
2589:
2575:
2574:
2544:
2527:10.2307/1970099
2508:
2490:
2459:
2408:10.2307/1970005
2355:
2339:
2334:
2326:
2322:
2317:
2313:
2302:
2298:
2293:
2289:
2284:
2280:
2275:
2271:
2267:
2246:
2231:
2218:
2208:
2191:
2178:
2158:
2147:
2139:
2131:
2097:
2093:
2078:
2060:
2056:
2050:
2045:
2041:
2033:
2030:
2029:
1986:
1982:
1970:
1965:
1961:
1947:
1944:
1943:
1901:
1897:
1885:
1879:
1876:
1875:
1866:
1846:
1833:
1819:
1802:
1796:
1786:
1740:
1733:
1696:
1691:
1664:
1642:
1617:
1609:simplicial sets
1588:
1572:
1566:
1560:
1511:
1502:
1488:
1477:
1470:
1457:
1447:
1438:
1428:
1415:
1406:
1399:
1382:
1373:
1364:
1355:
1333:. Furthermore,
1284:
1273:quasifibrations
1262:
1246:
1227:
1214:
1205:
1204:
1192:
1159:
1155:
1153:
1150:
1149:
1148:induced by the
1120:
1109:
1108:
1107:
1095:
1091:
1082:
1071:
1070:
1069:
1056:
1047:
1043:
1040:
1037:
1036:
1019:
1012:
1007:
1002:
1001:
999:
996:
995:
993:
986:
977:
970:
948:
944:
935:
931:
922:
917:
911:
908:
907:
884:
880:
871:
867:
865:
862:
861:
855:
844:
822:
763:
759:
733:
722:
721:
720:
699:
687:
676:
675:
674:
666:
662:
642:
631:
630:
629:
621:
617:
597:
586:
585:
584:
568:
565:
564:
542:
524:
504:
491:
482:
475:
438:
437:
425:
403:homology theory
401:∘ SP defines a
400:
394:
384:
373:
362:
351:
337:
296:
285:
277:
266:
255:
195:
174:
161:
144:
131:
121:
108:
95:
80:
49:quasifibrations
35:of a connected
29:homotopy groups
17:
12:
11:
5:
2598:
2588:
2587:
2573:
2572:
2563:
2554:
2543:
2542:External links
2540:
2539:
2538:
2512:
2506:
2493:
2488:
2463:
2457:
2439:Hatcher, Allen
2435:
2402:(2): 239–281,
2389:
2370:(2): 579–593,
2359:
2353:
2338:
2335:
2333:
2332:
2320:
2311:
2296:
2287:
2278:
2268:
2266:
2263:
2245:
2242:
2227:
2214:
2204:
2187:
2176:
2156:
2145:
2137:
2127:
2120:
2119:
2108:
2105:
2100:
2096:
2092:
2089:
2086:
2081:
2077:
2073:
2069:
2063:
2059:
2053:
2049:
2044:
2040:
2037:
2023:
2022:
2011:
2008:
2004:
2000:
1997:
1994:
1989:
1985:
1981:
1978:
1973:
1969:
1964:
1960:
1957:
1954:
1951:
1933:
1932:
1921:
1918:
1915:
1912:
1909:
1904:
1900:
1896:
1893:
1888:
1884:
1862:
1842:
1829:
1815:
1798:
1792:
1785:
1782:
1766:
1765:
1739:
1736:
1731:
1695:
1692:
1690:
1687:
1660:
1638:
1616:
1613:
1586:
1568:
1562:
1556:
1507:
1500:
1486:
1475:
1466:
1452:
1443:
1433:
1424:
1411:
1404:
1395:
1378:
1369:
1360:
1353:
1282:
1258:
1244:
1223:
1210:
1202:
1194:
1188:
1182:
1181:
1180:
1179:
1165:
1162:
1158:
1137:
1134:
1131:
1128:
1123:
1116:
1113:
1106:
1103:
1098:
1094:
1090:
1085:
1078:
1075:
1068:
1063:
1060:
1055:
1050:
1046:
1022:
1015:
1010:
1006:
991:
982:
975:
968:
951:
947:
943:
938:
934:
930:
925:
920:
916:
895:
892:
887:
883:
879:
874:
870:
853:
842:
836:
818:
813:
773:
766:
762:
757:
753:
750:
747:
742:
739:
736:
729:
726:
717:
713:
709:
706:
702:
698:
695:
690:
683:
680:
669:
665:
660:
656:
653:
650:
645:
638:
635:
624:
620:
615:
611:
608:
605:
600:
593:
590:
581:
577:
573:
537:
520:
514:
500:
487:
480:
473:
441:abelian groups
435:
427:
421:
396:
390:
383:
380:
371:
360:
349:
335:
294:
283:
275:
264:
253:
193:
170:
157:
140:
127:
124:
123:
117:
104:
91:
79:
76:
15:
9:
6:
4:
3:
2:
2597:
2586:
2583:
2582:
2580:
2571:
2570:StackExchange
2567:
2564:
2562:
2558:
2555:
2553:
2549:
2546:
2545:
2536:
2532:
2528:
2524:
2520:
2519:
2513:
2509:
2507:9780080872827
2503:
2499:
2494:
2491:
2485:
2481:
2477:
2473:
2469:
2464:
2460:
2454:
2450:
2446:
2445:
2440:
2436:
2433:
2429:
2425:
2421:
2417:
2413:
2409:
2405:
2401:
2397:
2396:
2390:
2387:
2383:
2378:
2373:
2369:
2365:
2360:
2356:
2350:
2346:
2341:
2340:
2329:
2324:
2315:
2309:
2305:
2300:
2291:
2282:
2273:
2269:
2262:
2260:
2255:
2251:
2241:
2239:
2235:
2230:
2226:
2222:
2217:
2212:
2207:
2203:
2199:
2195:
2190:
2186:
2182:
2174:
2170:
2166:
2162:
2155:
2151:
2143:
2136:≥ 2. But as π
2135:
2130:
2125:
2106:
2098:
2094:
2087:
2084:
2079:
2075:
2071:
2067:
2061:
2057:
2051:
2047:
2042:
2038:
2035:
2028:
2027:
2026:
2009:
2002:
1995:
1992:
1987:
1983:
1976:
1971:
1967:
1962:
1958:
1955:
1952:
1949:
1942:
1941:
1940:
1939:yields a map
1938:
1919:
1910:
1907:
1902:
1898:
1891:
1886:
1882:
1874:
1873:
1872:
1870:
1865:
1861:
1857:
1854:
1850:
1845:
1841:
1837:
1832:
1827:
1823:
1818:
1814:
1810:
1806:
1801:
1795:
1791:
1781:
1779:
1775:
1771:
1768:Note that SP(
1763:
1759:
1755:
1752:
1748:
1745:
1744:
1743:
1735:
1729:
1725:
1721:
1717:
1713:
1709:
1705:
1701:
1686:
1684:
1680:
1676:
1672:
1668:
1663:
1658:
1654:
1650:
1646:
1641:
1632:
1628:
1626:
1622:
1612:
1610:
1606:
1601:
1598:
1596:
1592:
1584:
1580:
1576:
1571:
1565:
1559:
1555:
1551:
1547:
1543:
1539:
1535:
1531:
1527:
1523:
1519:
1515:
1510:
1506:
1499:
1494:
1492:
1485:
1481:
1474:
1469:
1465:
1461:
1455:
1451:
1446:
1442:
1436:
1432:
1427:
1423:
1419:
1414:
1410:
1403:
1398:
1394:
1390:
1386:
1381:
1377:
1372:
1368:
1363:
1359:
1352:
1348:
1344:
1340:
1336:
1332:
1328:
1324:
1320:
1316:
1312:
1308:
1304:
1300:
1296:
1292:
1288:
1281:
1276:
1274:
1270:
1266:
1261:
1257:
1252:
1250:
1243:
1239:
1235:
1231:
1226:
1222:
1218:
1213:
1209:
1201:
1197:
1191:
1187:
1163:
1160:
1156:
1135:
1129:
1121:
1111:
1096:
1092:
1083:
1073:
1066:
1061:
1058:
1053:
1048:
1044:
1020:
1013:
1008:
1004:
990:
985:
981:
974:
967:
949:
945:
936:
932:
928:
923:
918:
914:
906:respectively
893:
885:
881:
877:
872:
868:
859:
858:direct system
852:
848:
841:
837:
834:
830:
826:
821:
817:
814:
811:
807:
803:
799:
795:
791:
787:
771:
764:
760:
755:
748:
740:
737:
734:
724:
711:
704:
700:
696:
688:
678:
667:
663:
658:
651:
643:
633:
622:
618:
613:
606:
598:
588:
575:
571:
562:
558:
554:
550:
546:
540:
536:
532:
528:
523:
519:
515:
512:
508:
503:
499:
495:
490:
486:
479:
472:
468:
464:
460:
456:
452:
451:
450:
449:
448:
446:
442:
434:
430:
424:
420:
416:
412:
408:
404:
399:
393:
389:
379:
377:
370:
366:
358:
355:
348:
344:
341:
332:
330:
326:
323:
319:
315:
311:
307:
303:
300:
292:
289:
281:
273:
270:
263:
259:
252:
248:
244:
240:
236:
233:
229:
226:
222:
218:
213:
211:
207:
203:
199:
192:
184:
180:
178:
173:
169:
165:
160:
155:
152:
148:
143:
139:
135:
130:
120:
116:
112:
107:
103:
99:
94:
89:
85:
82:
81:
75:
73:
69:
65:
61:
56:
54:
50:
46:
42:
38:
34:
30:
26:
22:
2561:MathOverflow
2552:MathOverflow
2516:
2500:. Elsevier.
2497:
2471:
2467:
2443:
2399:
2393:
2367:
2363:
2344:
2323:
2314:
2299:
2290:
2281:
2272:
2247:
2237:
2233:
2228:
2224:
2220:
2215:
2210:
2205:
2201:
2197:
2193:
2188:
2184:
2180:
2172:
2168:
2164:
2160:
2153:
2149:
2141:
2133:
2128:
2123:
2121:
2024:
1936:
1934:
1868:
1863:
1859:
1855:
1848:
1843:
1839:
1835:
1830:
1825:
1821:
1816:
1812:
1808:
1804:
1799:
1793:
1789:
1787:
1777:
1773:
1769:
1767:
1753:
1746:
1741:
1727:
1723:
1719:
1715:
1711:
1707:
1703:
1697:
1689:Applications
1682:
1678:
1674:
1670:
1666:
1661:
1656:
1652:
1648:
1644:
1639:
1636:
1624:
1620:
1618:
1602:
1599:
1590:
1582:
1578:
1574:
1569:
1563:
1557:
1553:
1549:
1545:
1541:
1537:
1533:
1529:
1525:
1521:
1517:
1516:∈ [0, 1) in
1513:
1508:
1504:
1497:
1495:
1490:
1483:
1479:
1472:
1467:
1463:
1459:
1453:
1449:
1444:
1440:
1434:
1430:
1425:
1421:
1417:
1412:
1408:
1401:
1396:
1392:
1388:
1384:
1379:
1375:
1370:
1366:
1361:
1357:
1350:
1346:
1342:
1334:
1326:
1322:
1318:
1314:
1310:
1306:
1302:
1298:
1294:
1290:
1286:
1279:
1277:
1268:
1264:
1259:
1255:
1253:
1248:
1241:
1237:
1233:
1229:
1224:
1220:
1216:
1211:
1207:
1199:
1195:
1189:
1185:
1183:
988:
983:
979:
972:
965:
850:
846:
839:
832:
828:
824:
819:
815:
809:
805:
801:
797:
793:
789:
785:
560:
556:
552:
548:
544:
538:
534:
530:
526:
521:
517:
506:
501:
497:
493:
488:
484:
477:
470:
466:
462:
458:
454:
444:
432:
428:
422:
418:
397:
391:
387:
385:
375:
368:
364:
356:
353:
346:
342:
339:
333:
328:
324:
317:
313:
309:
305:
301:
298:
290:
287:
279:
271:
268:
261:
257:
250:
246:
234:
231:
227:
224:
220:
216:
214:
209:
205:
201:
197:
190:
188:
176:
171:
167:
163:
158:
153:
146:
141:
137:
133:
128:
125:
118:
114:
110:
105:
101:
97:
92:
87:
83:
57:
24:
18:
2521:: 142–198,
1853:Moore space
831:≠ 1, where
78:The theorem
2474:: 91–101,
2337:References
1851:= 1 for a
1577:for every
827:) = 0 for
37:CW complex
2416:0003-486X
2386:256333418
2099:α
2088:
2080:α
2076:∏
2072:≅
2062:α
2052:α
2048:⋁
2039:
2007:→
1968:⋁
1959:
1953::
1917:→
1883:⋁
1493:) holds.
1254:Clearly,
1164:∗
1161:λ
1115:~
1105:→
1097:λ
1077:~
1067:
1062:→
1054::
1049:∗
1021:∗
1014:μ
1009:λ
950:μ
942:→
937:λ
929::
924:μ
919:λ
891:→
886:λ
878::
873:λ
772:…
765:∗
738:−
728:~
716:∂
682:~
668:∗
637:~
623:∗
592:~
580:∂
572:⋯
239:wedge sum
113:), where
90:one has π
2579:Category
2441:(2002).
1747:Theorem.
1489:() ≅ SP(
1356: :
756:→
712:→
659:→
614:→
576:→
45:functors
2535:1970099
2432:0097062
2424:1970005
2259:sheaves
1751:H-space
1681:) → SP(
1416:). For
1289:) → SP(
1236:) with
856:) is a
555:) with
469:, then
322:compact
312:) → SP(
308:) × SP(
237:be the
208:) → SP(
2533:
2504:
2486:
2455:
2430:
2422:
2414:
2384:
2351:
1567:with α
1391:) and
784:where
359:) or π
293:)) × π
282:)) ≅ π
189:where
23:, the
2531:JSTOR
2420:JSTOR
2382:S2CID
2265:Notes
2167:→ SP(
2144:) → π
1784:Proof
1722:into
1540:⊂ SP(
1383:= SP(
1285:: SP(
838:Let (
367:)) ≅
345:)) ≅
204:= SP(
2502:ISBN
2484:ISBN
2472:1425
2453:ISBN
2412:ISSN
2349:ISBN
2308:nLab
2250:Cech
2152:) =
2132:for
1824:) →
1788:Let
1726:and
1669:) ≅
1512:for
1439:and
1325:and
1267:) ≃
1219:) ≅
559:and
533:) →
496:) →
411:Thom
409:and
407:Dold
363:(SP(
338:(SP(
327:and
297:(SP(
286:(SP(
278:(SP(
166:) →
136:) →
100:) ≅
2568:on
2559:on
2550:on
2523:doi
2476:doi
2404:doi
2372:doi
2306:on
2252:or
2219:SP(
2148:SP(
1847:if
1834:if
1797:= π
1607:or
1251:).
1059:lim
453:If
395:= π
212:).
156:: π
132:SP(
96:SP(
19:In
2581::
2529:,
2482:,
2451:.
2447:.
2428:MR
2426:,
2418:,
2410:,
2400:67
2380:,
2368:14
2366:,
2232:,
2209:,
2192:,
2085:SP
2036:SP
1956:SP
1867:,
1820:,
1718:⊂
1714:,
1706:∩
1655:→
1651::
1623:=
1573:∈
1528:∈
1520:−
1456:−1
1448:−
1437:−1
1400:=
1365:→
1345:→
1317:,
1305:→
1301::
1242:h̃
1240:=
1232:;
1221:H̃
1208:h̃
1186:h̃
980:h̃
978:.
971:⊂
816:h̃
804:→
800::
792:→
788::
551:,
541:−1
535:h̃
518:h̃
498:h̃
485:h̃
483::
476:=
465:→
461::
457:≃
443:a
419:h̃
405:.
331:.
316:∨
230:∨
223:=
200::
168:H̃
138:H̃
115:H̃
102:H̃
74:.
55:.
2525::
2510:.
2478::
2461:.
2406::
2374::
2357:.
2238:X
2234:n
2229:n
2225:G
2223:(
2221:M
2216:n
2211:n
2206:n
2202:G
2200:(
2198:K
2194:n
2189:n
2185:G
2183:(
2181:M
2177:1
2173:f
2169:X
2165:X
2161:X
2159:(
2157:1
2154:H
2150:X
2146:1
2142:X
2140:(
2138:1
2134:n
2129:n
2124:f
2107:,
2104:)
2095:X
2091:(
2068:)
2058:X
2043:(
2010:X
2003:)
1999:)
1996:n
1993:,
1988:n
1984:G
1980:(
1977:M
1972:n
1963:(
1950:f
1937:X
1920:X
1914:)
1911:n
1908:,
1903:n
1899:G
1895:(
1892:M
1887:n
1869:n
1864:n
1860:G
1858:(
1856:M
1849:n
1844:1
1840:H
1836:n
1831:n
1826:X
1822:n
1817:n
1813:G
1811:(
1809:M
1805:X
1803:(
1800:n
1794:n
1790:G
1778:k
1774:Y
1770:Y
1764:.
1754:X
1732:*
1728:B
1724:A
1720:X
1716:B
1712:A
1708:B
1704:A
1683:S
1679:S
1675:S
1671:Z
1667:S
1665:(
1662:n
1657:X
1653:S
1649:f
1645:X
1643:(
1640:n
1625:S
1621:X
1591:a
1587:1
1585:α
1583:a
1579:t
1575:A
1570:t
1564:t
1561:α
1558:t
1554:x
1550:X
1546:A
1544:/
1542:X
1538:A
1536:/
1534:X
1530:A
1526:a
1522:A
1518:X
1514:t
1509:t
1505:x
1501:*
1498:p
1491:A
1487:*
1484:p
1480:X
1476:*
1473:p
1468:n
1464:B
1460:p
1454:n
1450:B
1445:n
1441:B
1435:n
1431:B
1426:n
1422:B
1418:n
1413:n
1409:B
1407:(
1405:*
1402:p
1397:n
1393:E
1389:A
1387:/
1385:X
1380:n
1376:B
1371:n
1367:B
1362:n
1358:E
1354:*
1351:p
1347:X
1343:A
1335:X
1327:A
1323:X
1319:A
1315:X
1311:A
1309:/
1307:X
1303:X
1299:p
1295:A
1293:/
1291:X
1287:X
1283:*
1280:p
1269:S
1265:S
1260:n
1256:h
1249:S
1247:(
1245:1
1238:G
1234:G
1230:X
1228:(
1225:n
1217:X
1215:(
1212:n
1203:0
1200:N
1198:∈
1196:n
1193:)
1190:n
1157:i
1136:,
1133:)
1130:X
1127:(
1122:n
1112:h
1102:)
1093:X
1089:(
1084:n
1074:h
1045:i
1005:i
992:λ
989:X
987:(
984:n
976:μ
973:X
969:λ
966:X
946:X
933:X
915:i
894:X
882:X
869:i
854:λ
851:X
847:X
843:λ
840:X
833:S
829:n
825:S
823:(
820:n
810:A
808:/
806:X
802:X
798:q
794:X
790:A
786:i
761:i
752:)
749:A
746:(
741:1
735:n
725:h
708:)
705:A
701:/
697:X
694:(
689:n
679:h
664:q
655:)
652:X
649:(
644:n
634:h
619:i
610:)
607:A
604:(
599:n
589:h
561:A
557:X
553:A
549:X
545:A
543:(
539:n
531:A
529:/
527:X
525:(
522:n
513:.
507:Y
505:(
502:n
494:X
492:(
489:n
481:*
478:g
474:*
471:f
467:Y
463:X
459:g
455:f
436:0
433:N
431:∈
429:n
426:)
423:n
398:n
392:n
388:h
376:X
374:(
372:1
369:H
365:X
361:1
357:H
354:C
352:(
350:1
347:H
343:H
340:C
336:1
329:Y
325:X
318:Y
314:X
310:Y
306:X
302:H
299:C
295:1
291:H
288:C
284:1
280:X
276:1
272:H
269:C
267:(
265:1
262:H
258:X
256:(
254:1
251:H
247:H
235:H
232:C
228:H
225:C
221:X
217:X
210:X
206:X
202:X
198:i
194:*
191:i
177:X
175:(
172:n
164:X
162:(
159:n
154:h
147:X
145:(
142:n
134:X
129:n
119:n
111:X
109:(
106:n
98:X
93:n
88:X
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.