357:
68:
60:
20:
52:
569:
622:
601:
139:
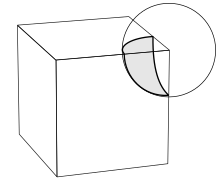
is thus a spherical polygon marked on this sphere. One advantage of this method is that the shape of the vertex figure is fixed (up to the scale of the sphere), whereas the method of intersecting with a plane can produce different shapes depending on the angle of the plane. Additionally, this method works for non-convex polyhedra.
580:
138:
Cromwell (1999) forms the vertex figure by intersecting the polyhedron with a sphere centered at the vertex, small enough that it intersects only edges and faces incident to the vertex. This can be visualized as making a spherical cut or scoop, centered on the vertex. The cut surface or vertex figure
125:
For an irregular polyhedron, cutting all edges incident to a given vertex at equal distances from the vertex may produce a figure that does not lie in a plane. A more general approach, valid for arbitrary convex polyhedra, is to make the cut along any plane which separates the given vertex from all
117:
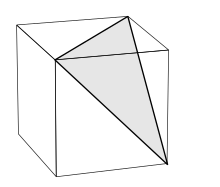
Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This is perhaps the most common approach, and the most easily understood. Different authors make the slice in different places. Wenninger (2003) cuts each
519:
Since the dual polytope of a regular polytope is also regular and represented by the Schläfli symbol indices reversed, it is easy to see the dual of the vertex figure is the cell of the dual polytope. For regular polyhedra, this is a special case of the
83:. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure.
126:
the other vertices, but is otherwise arbitrary. This construction determines the combinatorial structure of the vertex figure, similar to a set of connected vertices (see below), but not its precise geometry; it may be generalized to
147:
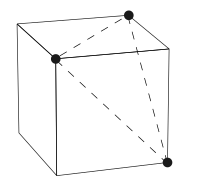
Many combinatorial and computational approaches (e.g. Skilling, 1975) treat a vertex figure as the ordered (or partially ordered) set of points of all the neighboring (connected via an edge) vertices to the given vertex.
696:
uniform polytopes will have a single edge type. In general, a uniform polytope can have as many edge types as active mirrors in the construction, since each active mirror produces one edge in the fundamental domain.
810:
around an edge. The other four edge figures are isosceles triangles on the base vertices of the pyramid. These represent the arrangement of two truncated cubes and one octahedron around the other edges.
638:
533:
90:(e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite
258:
notation, by listing the faces in sequence around the vertex. For example 3.4.4.4 is a vertex with one triangle and three squares, and it defines the uniform
130:
in any dimension. However, for non-convex polyhedra, there may not exist a plane near the vertex that cuts all of the faces incident to the vertex.
122:
construction cuts each connected edge at its midpoint. Other authors make the cut through the vertex at the other end of each edge.
980:
913:
286:
By considering the connectivity of these neighboring vertices, a vertex figure can be constructed for each vertex of a polytope:
1000:
946:
883:
309:
exists on or inside of a face of the original polytope connecting two alternate vertices from an original face.
677:. Edge figures are useful for expressing relations between the elements within regular and uniform polytopes.
231:
For nonconvex polyhedra, the vertex figure may also be nonconvex. Uniform polytopes, for instance, can have
345:
164:
comprises all the elements which are incident on the vertex; edges, faces, etc. More formally it is the (
995:
826:
783:
541:
506:
Example, the vertex figure for a hypercube {4,3,3}, the vertex figure is a regular tetrahedron {3,3}.
649:, and the others with one octahedron, and two truncated cubes. These can be seen as two types of
751:
is a polygon representing the arrangement of a set of facets around an edge. For example, the
86:
More precise formal definitions can vary quite widely, according to circumstance. For example
988:
748:
480:
255:
95:
8:
259:
251:(vertex-transitive) polytopes because one vertex figure can define the entire polytope.
118:
edge a unit distance from the vertex, as does
Coxeter (1948). For uniform polyhedra the
1022:
1017:
611:
476:
448:
377:
961:
942:
760:
590:
361:
291:
157:
76:
868:
806:. One is a square edge figure at the apex of the pyramid. This represents the four
689:
573:
548:. One octahedron and four truncated cubes meet at each vertex form a space-filling
244:
964:
193:. The geometrical vertex figure and the vertex star may be understood as distinct
820:
756:
693:
568:
521:
510:
381:
341:
313:
248:
127:
102:
795:
791:
615:
562:
545:
1011:
637:
532:
356:
67:
59:
19:
549:
369:
302:
232:
91:
51:
621:
119:
254:
For polyhedra with regular faces, a vertex figure can be represented in
799:
744:
594:
266:
222:
214:
80:
36:
969:
600:
579:
384:
and the vertex figure can be trivially extracted from this notation.
365:
344:
may be found from the original polyhedron's vertex figure using the "
106:
99:
40:
28:
470:
Example, the vertex figure for a cube {4,3}, is the triangle {3}.
331:... and so on to higher order elements in higher order polytopes.
218:
87:
265:
If the polytope is isogonal, the vertex figure will exist in a
35:, broadly speaking, is the figure exposed when a corner of a
941:
2008, John H. Conway, Heidi
Burgiel, Chaim Goodman-Strauss,
527:
513:{4,3,4}, the vertex figure is a regular octahedron {3,4}.
959:
376:
If a polytope is regular, it can be represented by a
920:
J. Skilling, The
Complete Set of Uniform Polyhedra,
387:
In general a regular polytope with Schläfli symbol {
142:
700:Regular polytopes (and honeycombs) have a single
298:coincides with a vertex of the original polytope.
1009:
213:−1)-polytope. For example, a vertex figure of a
16:Shape made by slicing off a corner of a polytope
823:- an abstract concept related to vertex figure.
704:which is also regular. For a regular polytope {
692:around a given edge. Regular and single-ringed
228:In general a vertex figure need not be planar.
688:−2)-polytope, representing the arrangement of
243:Vertex figures are especially significant for
281:
189:This set of elements is elsewhere known as a
893:H.S.M. Coxeter (et al.), Uniform Polyhedra,
335:
320:exists on or inside a cell of the original
340:For a uniform polyhedron, the face of the
743:In four dimensions, the edge figure of a
133:
653:. These are seen as the vertices of the
636:
531:
355:
66:
58:
50:
18:
528:An example vertex figure of a honeycomb
1010:
160:, the vertex figure at a given vertex
151:
55:"Whole-edge" vertex figure of the cube
978:
960:
235:for faces and/or for vertex figures.
200:
23:"Half-edge" vertex figure of the cube
536:truncated cubic honeycomb (partial).
351:
802:cells. Here there are two types of
238:
71:Point-set vertex figure of the cube
63:Spherical vertex figure of the cube
13:
645:has two edge types, one with four
112:
14:
1034:
953:
763:, and for a regular 4-polytope {
620:
599:
578:
567:
276:
143:As the set of connected vertices
877:
1001:Consistent Vertex Descriptions
869:Klitzing: Vertex figures, etc.
862:
853:
844:
632:
221:, and the vertex figure for a
197:of the same abstract section.
46:
1:
935:, CUP hbk (1983) ppbk (2003).
911:H.M. Cundy and A.P. Rollett,
832:
509:Also the vertex figure for a
105:and other higher-dimensional
917:, Oxford Univ. Press (1961).
7:
814:
10:
1039:
890:, Hbk (1948), ppbk (1973).
850:Coxeter, H. et al. (1954).
481:space-filling tessellation
282:From the adjacent vertices
96:space-filling tessellation
827:List of regular polytopes
784:truncated cubic honeycomb
643:truncated cubic honeycomb
542:truncated cubic honeycomb
495:}, the vertex figure is {
459:}, the vertex figure is {
360:The vertex figure of the
939:The Symmetries of Things
928:(1975) pp. 111–135.
901:(1954) pp. 401–450.
837:
522:Dorman Luke construction
336:Dorman Luke construction
985:Glossary for Hyperspace
540:The vertex figure of a
658:
537:
373:
205:A vertex figure of an
186:is the greatest face.
134:As a spherical polygon
72:
64:
56:
24:
949:(p289 Vertex figures)
640:
535:
359:
94:or, by extension, to
70:
62:
54:
22:
859:Skilling, J. (1975).
794:vertex figure, with
782:Less trivially, the
256:vertex configuration
75:Take some corner or
991:on 4 February 2007.
979:Olshevsky, George.
914:Mathematical Models
260:rhombicuboctahedron
152:Abstract definition
962:Weisstein, Eric W.
908:, CUP pbk. (1999).
775:} is the polygon {
659:
612:isosceles triangle
538:
477:regular 4-polytope
449:regular polyhedron
374:
201:General properties
158:abstract polytopes
73:
65:
57:
25:
947:978-1-56881-220-5
888:Regular Polytopes
630:
629:
362:great icosahedron
352:Regular polytopes
225:is a polyhedron.
209:-polytope is an (
156:In the theory of
1030:
992:
987:. Archived from
975:
974:
884:H. S. M. Coxeter
871:
866:
860:
857:
851:
848:
624:
603:
582:
574:Schlegel diagram
571:
555:
554:
544:is a nonuniform
407:} has cells as {
348:" construction.
239:Isogonal figures
128:convex polytopes
1038:
1037:
1033:
1032:
1031:
1029:
1028:
1027:
1008:
1007:
981:"Vertex figure"
965:"Vertex figure"
956:
880:
875:
874:
867:
863:
858:
854:
849:
845:
840:
835:
821:Simplicial link
817:
808:truncated cubes
790:{4,3,4}, has a
789:
757:cubic honeycomb
694:coxeter diagram
661:Related to the
647:truncated cubes
635:
625:
616:truncated cubes
604:
583:
572:
561:: A nonuniform
530:
511:cubic honeycomb
378:Schläfli symbol
354:
342:dual polyhedron
338:
324:-polytope (for
284:
279:
269:surface of the
241:
203:
184:
173:
154:
145:
136:
115:
113:As a flat slice
49:
43:is sliced off.
17:
12:
11:
5:
1036:
1026:
1025:
1020:
1004:
1003:
998:
996:Vertex Figures
993:
976:
955:
954:External links
952:
951:
950:
936:
931:M. Wenninger,
929:
918:
909:
902:
891:
879:
876:
873:
872:
861:
852:
842:
841:
839:
836:
834:
831:
830:
829:
824:
816:
813:
796:truncated cube
792:square pyramid
787:
755:for a regular
634:
631:
628:
627:
618:
607:
606:
597:
586:
585:
576:
565:
563:square pyramid
546:square pyramid
529:
526:
517:
516:
515:
514:
507:
473:
472:
471:
425:vertex figures
353:
350:
337:
334:
333:
332:
329:
310:
299:
283:
280:
278:
275:
240:
237:
202:
199:
182:
171:
153:
150:
144:
141:
135:
132:
114:
111:
48:
45:
15:
9:
6:
4:
3:
2:
1035:
1024:
1021:
1019:
1016:
1015:
1013:
1006:
1002:
999:
997:
994:
990:
986:
982:
977:
972:
971:
966:
963:
958:
957:
948:
944:
940:
937:
934:
930:
927:
923:
919:
916:
915:
910:
907:
904:P. Cromwell,
903:
900:
896:
892:
889:
885:
882:
881:
870:
865:
856:
847:
843:
828:
825:
822:
819:
818:
812:
809:
805:
801:
797:
793:
785:
780:
778:
774:
770:
766:
762:
759:{4,3,4} is a
758:
754:
750:
746:
741:
739:
735:
731:
727:
723:
719:
715:
711:
707:
703:
698:
695:
691:
687:
683:
678:
676:
675:vertex figure
672:
671:vertex figure
668:
664:
663:vertex figure
656:
655:vertex figure
652:
648:
644:
639:
623:
619:
617:
613:
609:
608:
602:
598:
596:
593:base from an
592:
589:Created as a
588:
587:
581:
577:
575:
570:
566:
564:
560:
559:Vertex figure
557:
556:
553:
551:
547:
543:
534:
525:
523:
512:
508:
505:
504:
502:
498:
494:
490:
486:
482:
478:
474:
469:
468:
466:
462:
458:
454:
450:
446:
445:
444:
442:
438:
434:
430:
426:
422:
418:
414:
410:
406:
402:
398:
394:
390:
385:
383:
380:and both the
379:
371:
367:
364:is a regular
363:
358:
349:
347:
343:
330:
327:
323:
319:
318:vertex figure
315:
311:
308:
307:vertex figure
304:
300:
297:
296:vertex figure
293:
289:
288:
287:
277:Constructions
274:
272:
268:
263:
261:
257:
252:
250:
246:
236:
234:
233:star polygons
229:
226:
224:
220:
216:
212:
208:
198:
196:
192:
187:
185:
178:
174:
167:
163:
159:
149:
140:
131:
129:
123:
121:
110:
108:
104:
101:
97:
93:
89:
84:
82:
78:
69:
61:
53:
44:
42:
38:
34:
33:vertex figure
30:
21:
1005:
989:the original
984:
968:
938:
932:
925:
921:
912:
905:
898:
894:
887:
878:Bibliography
864:
855:
846:
807:
804:edge figures
803:
781:
776:
772:
768:
764:
752:
742:
737:
733:
729:
725:
721:
717:
713:
709:
705:
701:
699:
685:
681:
679:
674:
670:
666:
662:
660:
654:
651:edge figures
650:
646:
642:
584:Perspective
558:
550:tessellation
539:
518:
500:
496:
492:
488:
484:
464:
460:
456:
452:
440:
436:
432:
428:
424:
420:
416:
412:
408:
404:
400:
396:
392:
388:
386:
375:
370:star polygon
339:
325:
321:
317:
306:
295:
285:
270:
264:
253:
242:
230:
227:
210:
206:
204:
195:realizations
194:
190:
188:
180:
176:
169:
168:−1)-section
165:
161:
155:
146:
137:
124:
116:
85:
74:
32:
26:
933:Dual Models
922:Phil. Trans
895:Phil. Trans
753:edge figure
749:3-honeycomb
726:edge figure
702:edge figure
684:will be a (
682:edge figure
667:edge figure
633:Edge figure
614:sides from
346:Dorman Luke
191:vertex star
120:Dorman Luke
47:Definitions
1012:Categories
833:References
800:octahedron
745:4-polytope
605:(3.3.3.3)
595:octahedron
267:hyperplane
247:and other
223:4-polytope
215:polyhedron
81:polyhedron
37:polyhedron
1023:Polytopes
1018:Polyhedra
970:MathWorld
906:Polyhedra
610:And four
366:pentagram
107:polytopes
815:See also
626:(3.8.8)
328:> 3).
273:-space.
249:isogonal
245:uniforms
179:, where
100:polytope
41:polytope
29:geometry
724:}, the
669:is the
423:}, and
316:of the
305:of the
294:of the
219:polygon
92:tilings
88:Coxeter
945:
924:. 278
897:. 246
761:square
690:facets
591:square
475:For a
467:-gon.
447:For a
372:{5/2}.
292:vertex
77:vertex
838:Notes
736:,...,
720:,...,
673:of a
665:, an
463:}, a
435:,...,
419:,...,
399:,...,
312:Each
301:Each
290:Each
217:is a
103:cells
98:with
79:of a
943:ISBN
798:and
728:is {
641:The
427:as {
382:cell
314:face
303:edge
31:, a
788:0,1
779:}.
747:or
740:}.
680:An
503:}.
479:or
443:}.
368:or
39:or
27:In
1014::
983:.
967:.
886:,
552:.
524:.
262:.
109:.
973:.
926:A
899:A
786:t
777:r
773:r
771:,
769:q
767:,
765:p
738:z
734:s
732:,
730:r
722:z
718:s
716:,
714:r
712:,
710:q
708:,
706:p
686:n
657:.
501:r
499:,
497:q
493:r
491:,
489:q
487:,
485:p
483:{
465:q
461:q
457:q
455:,
453:p
451:{
441:z
439:,
437:y
433:c
431:,
429:b
421:y
417:c
415:,
413:b
411:,
409:a
405:z
403:,
401:y
397:c
395:,
393:b
391:,
389:a
326:n
322:n
271:n
211:n
207:n
183:n
181:F
177:V
175:/
172:n
170:F
166:n
162:V
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.