20:
762:
3467:
2074:
3479:
360:
2369:(also called ′slice genus′) of a knot is therefore defined as the smallest genus of an embedded surface in 4-space of which the knot is the boundary. As before, we distinguish the topological and smooth 4-genus. Knots with 4-genus 0 are slice knots because a disk, the simplest surface, has genus 0. The 4-genus is always smaller or equal to the knot's
2348:
This is useful because the critical points with respect to the radial function r carry geometrical meaning. At saddle points, trivial components are added or destroyed (band moves, also called fusion and fission). For slice knots any number of these band moves are possible, whereas for ribbon knots
2340:
This can be illustrated also with the first figure at the top of this article: If a small disk at the local minimum on the bottom left is cut out then the boundary of the surface at this place is a trivial knot and the surface is a cylinder. At the other end of the cylinder we have a slice knot. If
2077:
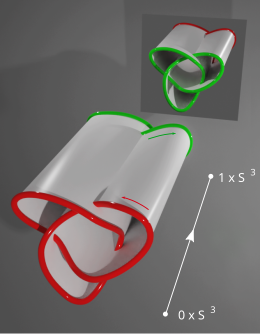
Top: The composition of two knot concordances shows the transitivity in a geometric way. Bottom: A concordance of genus 1 between two knots. If the knot on the left is trivial then the knot on the right has a smooth 4-genus of 0 or 1 — it is the boundary of an embedded surface of genus 1 but could
765:
Using the trefoil knot we illustrate the reflexivity of the concordance relation: every knot is concordant to itself. In the definition of concordance two reversions of orientations occur: The knot orientation is reversed (green and red arrow) and also the orientation of 3-space. The effect of the
2376:
Examples for knots with different values for their topological and smooth 4-genus are listed in the following table. The Conway knot 11n34 is, as already mentioned, the first example in the knot tables for a topologically but not smoothly slice knot. Judging from the values in the table we could
374:
Note, that the disk in the illustration on the right does not have self-intersections in 4-space. These only occur in the projection to three-dimensional space. Therefore, the disk is ′correctly′ embedded at every point but not at the singularity (it is not locally-flat there).
770:
Every ribbon knot is a smoothly slice knot because—with the exception of the ribbon singularities—the knot already bounds an embedded disk (in 3-space). The ribbon singularities may be deformed in a small neighbourhood into 4-space so that the disk is embedded.
2000:. Since the determinant of the figure-eight knot is 5, which is not a square number, this knot is not slice and it follows that its order in the concordance group is 2. Of course, knots with a finite order in the concordance group always have signature 0.
2377:
conclude that the smooth and the topological 4-genus always differ by 1, when they are not equal. This is not the case, however, and the difference can be arbitrarily large. It is not known, though, (as of 2017), whether there are
343:
Every smoothly slice knot is topologically slice because a smoothly embedded disk is locally flat. Usually, smoothly slice knots are also just called slice. Both types of slice knots are important in 3- and 4-dimensional topology.
341:
251:
2065:) are always topologically slice, but not necessarily smoothly slice (the Conway knot is an example for that). Rasmussen's s-invariant vanishes for smoothly slice, but in general not for topologically slice knots.
2352:
In the illustration on the right the geometrical description of the concordance is rotated by 90° and the parameter r is renamed to t. This name fits well to a time interpretation of a surface ′movie′.
2308:
and therefore two mirrored trefoils are shown as boundary of the cylinder. Connecting the two knots by cutting out a strip from the cylinder yields a disk, showing that for all knots the connected sum
1998:
1550:
371:
over the knot which is a disk in the 4-ball with the required property with the exception that it is not locally-flat or smooth at the singularity (it works for the trivial knot, though).
1708:
168:
1630:
1590:
471:
2185:
78:
2275:
2230:
2063:
1923:
1766:
1465:
814:
1383:. Up to this crossing number there are no topologically slice knots which are not smoothly slice. Starting with crossing number 11 there is such an example, however: The
421:
2335:
1494:
561:
2525:
2497:
2469:
2441:
2413:
1381:
1354:
1327:
1300:
1273:
1246:
753:
which is called the (topological or smooth) knot concordance group. The neutral element in this group is the set of slice knots (topological or smooth, respectively).
1219:
1192:
1165:
1138:
1111:
1084:
1057:
1839:
1030:
1003:
976:
949:
922:
501:
2552:
2302:
2134:
2107:
2025:
1872:
1427:
895:
868:
841:
743:
716:
689:
662:
635:
608:
532:
117:
1813:
1731:
581:
263:
2232:). The orientations of the two knots have to be consistent to the cylinder's orientation, which is illustrated in the third figure. The boundary of
176:
2082:
As an alternative to the above definition of concordance using slice knots there is also a second equivalent definition. Two oriented knots
2030:
On the other hand, invariants with different properties for the two concordance variants exist: Knots with trivial
Alexander polynomial (
351:
and it is an open question whether there are any smoothly slice knots which are not ribbon knots (′Slice-ribbon conjecture′).
2844:
1928:
3412:
3331:
1775:
is an invariant of concordance classes and the signature of slice knots is zero. Furthermore, the signature map is a
1499:
2878:
2373:
because this invariant is defined using
Seifert surfaces which are embedded already in three-dimensional space.
3505:
2711:
1391:) is a topologically but not smoothly slice knot. On the other hand, the Kinoshita-Terasaka knot, a so-called ′
1647:
3326:
3321:
3197:
2718:, in: A. Marin, L. Guillou: A la recherche de la topologie perdue, Progress in Mathematics, Birkhäuser 1986.
3483:
2898:
1400:
367:
The conditions locally-flat or smooth are essential in the definition: For every knot we can construct the
130:
2960:
1595:
1555:
433:
27:, showing minima, saddles and a maximum, and as an illustration a movie for the Kinoshita–Terasaka knot
3030:
3025:
2966:
2837:
2305:
2139:
428:
50:
2812:
2337:
is slice. In both definitions a knot is slice if and only if it is concordant to the trivial knot.
2235:
2190:
2033:
1885:
1736:
1432:
781:
534:
where in addition the orientation is reversed. The relationship ′concordant′ is reflexive because
3158:
2370:
386:
2311:
1470:
537:
473:
is slice. In the same way as before, we distinguish topologically and smoothly concordant. With
3372:
3341:
1392:
2643:
2503:
2475:
2447:
2419:
2391:
1359:
1332:
1305:
1278:
1251:
1224:
3202:
1197:
1170:
1143:
1116:
1089:
1062:
1035:
749:. The equivalence classes together with the connected sum of knots as operation then form an
1818:
1008:
981:
954:
927:
900:
476:
3471:
3242:
2830:
2787:
2531:
2280:
2112:
2085:
2007:
1850:
1788:
1641:
1405:
873:
846:
819:
746:
721:
694:
667:
640:
613:
586:
510:
95:
2740:
The mirror variants of the knots have to be chosen in a way that the total signature is 0.
2004:
For both variants of the concordance group it is unknown whether elements of finite order
1733:
with integer coefficients (Fox-Milnor condition). It follows that the knot's determinant (
8:
3279:
3262:
2362:
1772:
1467:
are known. Composite slice knots up to crossing number 12 are, besides those of the form
254:
1783:: The signature of the sum of two concordance classes is the sum of the two signatures.
3300:
3247:
2861:
2857:
2341:
the disk (or cylinder) is smoothly embedded it can be slightly deformed to a so-called
1798:
1716:
1711:
1388:
566:
258:
36:
3397:
3346:
3296:
3252:
3212:
3207:
3125:
1845:
3432:
3257:
3153:
2888:
2655:
1640:
The following properties are valid for topologically and smoothly slice knots: The
19:
3392:
3356:
3291:
3237:
3192:
3185:
3075:
2987:
2870:
2691:
1879:
368:
2822:
2682:
for the notation and list of slice knots (genus-4D = 0 and genus-4D (Top.) = 0).
2658: – Link equivalence relation weaker than isotopy but stronger than homotopy
336:{\displaystyle B^{4}=\{\mathbf {x} \in \mathbb {R} ^{4}:|\mathbf {x} |\leq 1\}.}
3452:
3351:
3313:
3232:
3145:
3020:
3012:
2972:
2639:
2361:
An analogous definition as for slice knots may be done with surfaces of larger
2136:
are concordant if they are the boundary of a (locally flat or smooth) cylinder
761:
120:
3499:
3387:
3175:
3168:
3163:
2707:
1429:, not slice. All topologically and smoothly slice knots with crossing number
750:
39:
in 3-dimensional space that bounds an embedded disk in 4-dimensional space.
3402:
3382:
3286:
3269:
3065:
3002:
2342:
1792:
1776:
246:{\displaystyle S^{3}=\{\mathbf {x} \in \mathbb {R} ^{4}:|\mathbf {x} |=1\}}
24:
3417:
3180:
3085:
2954:
2934:
2924:
2916:
2908:
2853:
2753:
2366:
1875:
1795:
is ±2 and the signature of the concordance class of the connected sum of
1384:
504:
348:
3437:
3377:
3274:
3227:
3222:
3217:
3047:
2944:
1396:
775:
124:
2068:
3442:
3110:
2749:
2679:
89:
2800:
On 2-bridge knots with differing smooth and topological slice genera
2073:
1787:
It follows that the concordance group contains elements of infinite
3427:
3037:
347:
Smoothly slice knots are often illustrated using knots diagrams of
171:
1780:
2817:, Banff International Research Station, 2017, Problem 25, p. 12.
3447:
3095:
3055:
359:
3336:
2758:
Singularities of 2-Spheres in 4-Space and
Cobordism of Knots.
1844:
The concordance group also contains elements of order 2: The
378:
3407:
2629:, Chapter 7 in „Handbook of Knot Theory“, Elsevier, 2005
583:. It is also possible to show that it is transitive: if
2782:
For the orientation of a product see Tammo tom Dieck:
1993:{\displaystyle 4_{1}\sharp 4_{1}=4_{1}\sharp -4_{1}=0}
2534:
2506:
2478:
2450:
2422:
2394:
2349:
only fusions may occur and fissions are not allowed.
2314:
2283:
2238:
2193:
2142:
2115:
2088:
2036:
2010:
1931:
1888:
1853:
1821:
1801:
1739:
1719:
1650:
1598:
1558:
1502:
1473:
1435:
1408:
1362:
1335:
1308:
1281:
1254:
1227:
1200:
1173:
1146:
1119:
1092:
1065:
1038:
1011:
984:
957:
930:
903:
876:
849:
822:
784:
724:
697:
670:
643:
616:
589:
569:
540:
513:
479:
436:
389:
266:
179:
133:
98:
53:
2727:Ribbon diagrams for them can be found in: C. Lamm,
2069:
Geometrical description of the concordance relation
2546:
2519:
2491:
2463:
2435:
2407:
2329:
2296:
2269:
2224:
2179:
2128:
2101:
2057:
2019:
1992:
1917:
1866:
1833:
1807:
1760:
1725:
1702:
1624:
1584:
1544:
1488:
1459:
1421:
1375:
1348:
1321:
1294:
1267:
1240:
1213:
1186:
1159:
1132:
1105:
1078:
1051:
1024:
997:
970:
943:
916:
889:
862:
835:
808:
737:
710:
683:
656:
629:
602:
575:
555:
526:
495:
465:
415:
335:
245:
162:
111:
72:
2852:
2802:, Proc. Amer. Math. Soc. 144, p. 5435–5442, 2016.
745:. Since the relation is also symmetric, it is an
3497:
1545:{\displaystyle 6_{1}\sharp 3_{1}\sharp -3_{1}}
2838:
2786:, EMS Textbooks in Mathematics, 2008 (online
2644:Slice knots: knot theory in the 4th dimension
2814:Thirty Years of Floer Theory for 3-manifolds
327:
280:
240:
193:
16:Knot that bounds an embedded disk in 4-space
2698:Ann. of Math. 191, No. 2, p. 581–591, 2020.
2845:
2831:
379:Slice knots and the knot concordance group
1399:are, except for the trivial knot and the
1395:′ of the Conway knot, is smoothly slice.
293:
206:
2729:The Search for Nonsymmetric Ribbon Knots
2072:
1703:{\displaystyle \Delta (t)=f(t)f(t^{-1})}
760:
358:
18:
3498:
2771:Khovanov homology and the slice genus.
2627:A Survey of Classical Knot Concordance
2615:, Publish or Perish, 1976, Chapter 8.E
2826:
2622:, Carus Mathematical Monographs, 1993
3478:
354:
163:{\displaystyle S^{3}=\partial B^{4}}
2760:Osaka J. Math. 3, p. 257–267, 1966.
2674:See C. Livingston and A. H. Moore:
1925:. In the concordance group we find
13:
2731:, Exp. Math. 30, p. 349–363, 2021.
2680:https://knotinfo.math.indiana.edu/
2676:KnotInfo: Table of Knot Invariants
2318:
2037:
1968:
1942:
1743:
1651:
1644:of a slice knot can be written as
1625:{\displaystyle 3_{1}\sharp 8_{11}}
1609:
1585:{\displaystyle 3_{1}\sharp 8_{10}}
1569:
1526:
1513:
1477:
544:
466:{\displaystyle K_{1}\sharp -K_{2}}
447:
147:
14:
3517:
2773:Inv. Math. 182, p. 419–447, 2010.
2633:
1552:, the two more interesting knots
3477:
3466:
3465:
2381:knots with a difference > 1.
312:
284:
225:
197:
2805:
2605:
774:There are 21 non-trivial slice
766:latter is the knot's mirroring.
3332:Dowker–Thistlethwaite notation
2792:
2776:
2763:
2743:
2734:
2721:
2701:
2685:
2668:
2264:
2252:
2219:
2207:
2180:{\displaystyle C=S^{1}\times }
2174:
2162:
2046:
2040:
1779:from concordance group to the
1755:
1746:
1697:
1681:
1675:
1669:
1660:
1654:
1448:
1442:
797:
791:
317:
307:
230:
220:
88:, if it is the boundary of an
73:{\displaystyle K\subset S^{3}}
1:
2696:The Conway knot is not slice.
2662:
1635:
42:
2716:Cobordism of Classical Knots
2270:{\displaystyle S^{3}\times }
2225:{\displaystyle S^{3}\times }
2187:(in the 4-dimensional space
2058:{\displaystyle \Delta (t)=1}
1918:{\displaystyle 4_{1}=-4_{1}}
1761:{\displaystyle =\Delta (-1)}
1460:{\displaystyle cr(K)\leq 12}
809:{\displaystyle cr(K)\leq 10}
127:, respectively. Here we use
7:
2649:
756:
416:{\displaystyle K_{1},K_{2}}
10:
3522:
2811:See the conference report
2356:
2330:{\displaystyle K\sharp -K}
1489:{\displaystyle K\sharp -K}
556:{\displaystyle K\sharp -K}
363:Cone over the trefoil knot
3461:
3365:
3322:Alexander–Briggs notation
3309:
3144:
3046:
3011:
2869:
2520:{\displaystyle 10_{161}}
2492:{\displaystyle 10_{154}}
2464:{\displaystyle 10_{152}}
2436:{\displaystyle 10_{145}}
2408:{\displaystyle 10_{139}}
1882:, and therefore we have
1376:{\displaystyle 10_{155}}
1349:{\displaystyle 10_{153}}
1322:{\displaystyle 10_{140}}
1295:{\displaystyle 10_{137}}
1268:{\displaystyle 10_{129}}
1241:{\displaystyle 10_{123}}
563:is slice for every knot
257:of the four-dimensional
82:topologically slice knot
3413:List of knots and links
2961:Kinoshita–Terasaka knot
1214:{\displaystyle 10_{99}}
1187:{\displaystyle 10_{87}}
1160:{\displaystyle 10_{75}}
1133:{\displaystyle 10_{48}}
1106:{\displaystyle 10_{42}}
1079:{\displaystyle 10_{35}}
1052:{\displaystyle 10_{22}}
23:A smooth slice disk in
2548:
2521:
2493:
2465:
2437:
2409:
2331:
2298:
2271:
2226:
2181:
2130:
2103:
2079:
2059:
2021:
1994:
1919:
1868:
1835:
1834:{\displaystyle \pm 2n}
1809:
1768:) is a square number.
1762:
1727:
1704:
1626:
1586:
1546:
1490:
1461:
1423:
1377:
1350:
1323:
1296:
1269:
1242:
1215:
1188:
1161:
1134:
1107:
1080:
1053:
1026:
1025:{\displaystyle 10_{3}}
999:
998:{\displaystyle 9_{46}}
972:
971:{\displaystyle 9_{41}}
945:
944:{\displaystyle 9_{27}}
918:
917:{\displaystyle 8_{20}}
891:
864:
837:
810:
767:
739:
712:
685:
658:
631:
604:
577:
557:
528:
497:
496:{\displaystyle -K_{2}}
467:
417:
364:
337:
247:
164:
113:
74:
28:
3506:Slice knots and links
3203:Finite type invariant
2798:P. Feller, D. McCoy:
2549:
2547:{\displaystyle 11n34}
2522:
2494:
2466:
2438:
2410:
2332:
2299:
2297:{\displaystyle S^{3}}
2272:
2227:
2182:
2131:
2129:{\displaystyle K_{2}}
2104:
2102:{\displaystyle K_{1}}
2076:
2060:
2022:
2020:{\displaystyle >2}
1995:
1920:
1869:
1867:{\displaystyle 4_{1}}
1836:
1810:
1791:: The signature of a
1763:
1728:
1705:
1627:
1587:
1547:
1491:
1462:
1424:
1422:{\displaystyle 6_{1}}
1378:
1351:
1324:
1297:
1270:
1243:
1216:
1189:
1162:
1135:
1108:
1081:
1054:
1027:
1000:
973:
946:
919:
892:
890:{\displaystyle 8_{9}}
865:
863:{\displaystyle 8_{8}}
838:
836:{\displaystyle 6_{1}}
811:
778:with crossing number
764:
740:
738:{\displaystyle K_{3}}
713:
711:{\displaystyle K_{1}}
686:
684:{\displaystyle K_{3}}
659:
657:{\displaystyle K_{2}}
632:
630:{\displaystyle K_{2}}
605:
603:{\displaystyle K_{1}}
578:
558:
529:
527:{\displaystyle K_{2}}
498:
468:
418:
362:
338:
248:
165:
114:
112:{\displaystyle B^{4}}
75:
22:
2625:Charles Livingston:
2618:Charles Livingston:
2532:
2504:
2476:
2448:
2420:
2392:
2312:
2281:
2236:
2191:
2140:
2113:
2086:
2034:
2008:
1929:
1886:
1851:
1841:and therefore not 0.
1819:
1799:
1737:
1717:
1648:
1642:Alexander polynomial
1596:
1556:
1500:
1471:
1433:
1406:
1360:
1333:
1306:
1279:
1252:
1225:
1198:
1171:
1144:
1117:
1090:
1063:
1036:
1009:
982:
955:
928:
901:
874:
847:
820:
782:
747:equivalence relation
722:
695:
668:
641:
614:
587:
567:
538:
511:
477:
434:
387:
264:
177:
131:
96:
51:
3373:Alexander's theorem
383:Two oriented knots
92:disk in the 4-ball
86:smoothly slice knot
2784:Algebraic Topology
2544:
2517:
2489:
2461:
2433:
2405:
2327:
2294:
2267:
2222:
2177:
2126:
2099:
2080:
2078:also bound a disk.
2055:
2017:
1990:
1915:
1864:
1831:
1805:
1758:
1723:
1712:Laurent polynomial
1700:
1622:
1582:
1542:
1486:
1457:
1419:
1389:John Horton Conway
1373:
1346:
1319:
1292:
1265:
1238:
1211:
1184:
1157:
1130:
1103:
1076:
1049:
1022:
995:
968:
941:
914:
887:
860:
833:
806:
768:
735:
708:
681:
654:
627:
600:
573:
553:
524:
493:
463:
413:
365:
333:
243:
160:
109:
70:
29:
3493:
3492:
3347:Reidemeister move
3213:Khovanov homology
3208:Hyperbolic volume
2769:Jacob Rasmussen:
2603:
2602:
1846:figure-eight knot
1808:{\displaystyle n}
1726:{\displaystyle f}
718:is concordant to
664:is concordant to
610:is concordant to
576:{\displaystyle K}
355:Cone construction
37:mathematical knot
3513:
3481:
3480:
3469:
3468:
3433:Tait conjectures
3136:
3135:
3121:
3120:
3106:
3105:
2998:
2997:
2983:
2982:
2967:(−2,3,7) pretzel
2847:
2840:
2833:
2824:
2823:
2818:
2809:
2803:
2796:
2790:
2780:
2774:
2767:
2761:
2747:
2741:
2738:
2732:
2725:
2719:
2705:
2699:
2689:
2683:
2672:
2656:Link concordance
2558:4-genus (smooth)
2553:
2551:
2550:
2545:
2526:
2524:
2523:
2518:
2516:
2515:
2498:
2496:
2495:
2490:
2488:
2487:
2470:
2468:
2467:
2462:
2460:
2459:
2442:
2440:
2439:
2434:
2432:
2431:
2414:
2412:
2411:
2406:
2404:
2403:
2384:
2383:
2336:
2334:
2333:
2328:
2303:
2301:
2300:
2295:
2293:
2292:
2276:
2274:
2273:
2268:
2248:
2247:
2231:
2229:
2228:
2223:
2203:
2202:
2186:
2184:
2183:
2178:
2158:
2157:
2135:
2133:
2132:
2127:
2125:
2124:
2108:
2106:
2105:
2100:
2098:
2097:
2064:
2062:
2061:
2056:
2026:
2024:
2023:
2018:
1999:
1997:
1996:
1991:
1983:
1982:
1967:
1966:
1954:
1953:
1941:
1940:
1924:
1922:
1921:
1916:
1914:
1913:
1898:
1897:
1873:
1871:
1870:
1865:
1863:
1862:
1840:
1838:
1837:
1832:
1814:
1812:
1811:
1806:
1767:
1765:
1764:
1759:
1732:
1730:
1729:
1724:
1709:
1707:
1706:
1701:
1696:
1695:
1631:
1629:
1628:
1623:
1621:
1620:
1608:
1607:
1591:
1589:
1588:
1583:
1581:
1580:
1568:
1567:
1551:
1549:
1548:
1543:
1541:
1540:
1525:
1524:
1512:
1511:
1495:
1493:
1492:
1487:
1466:
1464:
1463:
1458:
1428:
1426:
1425:
1420:
1418:
1417:
1382:
1380:
1379:
1374:
1372:
1371:
1355:
1353:
1352:
1347:
1345:
1344:
1328:
1326:
1325:
1320:
1318:
1317:
1301:
1299:
1298:
1293:
1291:
1290:
1274:
1272:
1271:
1266:
1264:
1263:
1247:
1245:
1244:
1239:
1237:
1236:
1220:
1218:
1217:
1212:
1210:
1209:
1193:
1191:
1190:
1185:
1183:
1182:
1166:
1164:
1163:
1158:
1156:
1155:
1139:
1137:
1136:
1131:
1129:
1128:
1112:
1110:
1109:
1104:
1102:
1101:
1085:
1083:
1082:
1077:
1075:
1074:
1058:
1056:
1055:
1050:
1048:
1047:
1031:
1029:
1028:
1023:
1021:
1020:
1004:
1002:
1001:
996:
994:
993:
977:
975:
974:
969:
967:
966:
950:
948:
947:
942:
940:
939:
923:
921:
920:
915:
913:
912:
896:
894:
893:
888:
886:
885:
869:
867:
866:
861:
859:
858:
842:
840:
839:
834:
832:
831:
815:
813:
812:
807:
744:
742:
741:
736:
734:
733:
717:
715:
714:
709:
707:
706:
690:
688:
687:
682:
680:
679:
663:
661:
660:
655:
653:
652:
636:
634:
633:
628:
626:
625:
609:
607:
606:
601:
599:
598:
582:
580:
579:
574:
562:
560:
559:
554:
533:
531:
530:
525:
523:
522:
502:
500:
499:
494:
492:
491:
472:
470:
469:
464:
462:
461:
446:
445:
422:
420:
419:
414:
412:
411:
399:
398:
342:
340:
339:
334:
320:
315:
310:
302:
301:
296:
287:
276:
275:
252:
250:
249:
244:
233:
228:
223:
215:
214:
209:
200:
189:
188:
169:
167:
166:
161:
159:
158:
143:
142:
118:
116:
115:
110:
108:
107:
80:is said to be a
79:
77:
76:
71:
69:
68:
3521:
3520:
3516:
3515:
3514:
3512:
3511:
3510:
3496:
3495:
3494:
3489:
3457:
3361:
3327:Conway notation
3311:
3305:
3292:Tricolorability
3140:
3134:
3131:
3130:
3129:
3119:
3116:
3115:
3114:
3104:
3101:
3100:
3099:
3091:
3081:
3071:
3061:
3042:
3021:Composite knots
3007:
2996:
2993:
2992:
2991:
2988:Borromean rings
2981:
2978:
2977:
2976:
2950:
2940:
2930:
2920:
2912:
2904:
2894:
2884:
2865:
2851:
2821:
2810:
2806:
2797:
2793:
2781:
2777:
2768:
2764:
2748:
2744:
2739:
2735:
2726:
2722:
2706:
2702:
2692:Lisa Piccirillo
2690:
2686:
2673:
2669:
2665:
2652:
2636:
2613:Knots and Links
2608:
2533:
2530:
2529:
2511:
2507:
2505:
2502:
2501:
2483:
2479:
2477:
2474:
2473:
2455:
2451:
2449:
2446:
2445:
2427:
2423:
2421:
2418:
2417:
2399:
2395:
2393:
2390:
2389:
2359:
2313:
2310:
2309:
2304:with different
2288:
2284:
2282:
2279:
2278:
2243:
2239:
2237:
2234:
2233:
2198:
2194:
2192:
2189:
2188:
2153:
2149:
2141:
2138:
2137:
2120:
2116:
2114:
2111:
2110:
2093:
2089:
2087:
2084:
2083:
2071:
2035:
2032:
2031:
2009:
2006:
2005:
1978:
1974:
1962:
1958:
1949:
1945:
1936:
1932:
1930:
1927:
1926:
1909:
1905:
1893:
1889:
1887:
1884:
1883:
1858:
1854:
1852:
1849:
1848:
1820:
1817:
1816:
1800:
1797:
1796:
1738:
1735:
1734:
1718:
1715:
1714:
1688:
1684:
1649:
1646:
1645:
1638:
1616:
1612:
1603:
1599:
1597:
1594:
1593:
1576:
1572:
1563:
1559:
1557:
1554:
1553:
1536:
1532:
1520:
1516:
1507:
1503:
1501:
1498:
1497:
1472:
1469:
1468:
1434:
1431:
1430:
1413:
1409:
1407:
1404:
1403:
1367:
1363:
1361:
1358:
1357:
1340:
1336:
1334:
1331:
1330:
1313:
1309:
1307:
1304:
1303:
1286:
1282:
1280:
1277:
1276:
1259:
1255:
1253:
1250:
1249:
1232:
1228:
1226:
1223:
1222:
1205:
1201:
1199:
1196:
1195:
1178:
1174:
1172:
1169:
1168:
1151:
1147:
1145:
1142:
1141:
1124:
1120:
1118:
1115:
1114:
1097:
1093:
1091:
1088:
1087:
1070:
1066:
1064:
1061:
1060:
1043:
1039:
1037:
1034:
1033:
1016:
1012:
1010:
1007:
1006:
989:
985:
983:
980:
979:
962:
958:
956:
953:
952:
935:
931:
929:
926:
925:
908:
904:
902:
899:
898:
881:
877:
875:
872:
871:
854:
850:
848:
845:
844:
827:
823:
821:
818:
817:
783:
780:
779:
759:
729:
725:
723:
720:
719:
702:
698:
696:
693:
692:
675:
671:
669:
666:
665:
648:
644:
642:
639:
638:
621:
617:
615:
612:
611:
594:
590:
588:
585:
584:
568:
565:
564:
539:
536:
535:
518:
514:
512:
509:
508:
487:
483:
478:
475:
474:
457:
453:
441:
437:
435:
432:
431:
423:are said to be
407:
403:
394:
390:
388:
385:
384:
381:
357:
316:
311:
306:
297:
292:
291:
283:
271:
267:
265:
262:
261:
229:
224:
219:
210:
205:
204:
196:
184:
180:
178:
175:
174:
154:
150:
138:
134:
132:
129:
128:
103:
99:
97:
94:
93:
64:
60:
52:
49:
48:
45:
17:
12:
11:
5:
3519:
3509:
3508:
3491:
3490:
3488:
3487:
3475:
3462:
3459:
3458:
3456:
3455:
3453:Surgery theory
3450:
3445:
3440:
3435:
3430:
3425:
3420:
3415:
3410:
3405:
3400:
3395:
3390:
3385:
3380:
3375:
3369:
3367:
3363:
3362:
3360:
3359:
3354:
3352:Skein relation
3349:
3344:
3339:
3334:
3329:
3324:
3318:
3316:
3307:
3306:
3304:
3303:
3297:Unknotting no.
3294:
3289:
3284:
3283:
3282:
3272:
3267:
3266:
3265:
3260:
3255:
3250:
3245:
3235:
3230:
3225:
3220:
3215:
3210:
3205:
3200:
3195:
3190:
3189:
3188:
3178:
3173:
3172:
3171:
3161:
3156:
3150:
3148:
3142:
3141:
3139:
3138:
3132:
3123:
3117:
3108:
3102:
3093:
3089:
3083:
3079:
3073:
3069:
3063:
3059:
3052:
3050:
3044:
3043:
3041:
3040:
3035:
3034:
3033:
3028:
3017:
3015:
3009:
3008:
3006:
3005:
3000:
2994:
2985:
2979:
2970:
2964:
2958:
2952:
2948:
2942:
2938:
2932:
2928:
2922:
2918:
2914:
2910:
2906:
2902:
2896:
2892:
2886:
2882:
2875:
2873:
2867:
2866:
2850:
2849:
2842:
2835:
2827:
2820:
2819:
2804:
2791:
2775:
2762:
2742:
2733:
2720:
2712:Cameron Gordon
2700:
2684:
2666:
2664:
2661:
2660:
2659:
2651:
2648:
2647:
2646:
2640:Peter Teichner
2635:
2634:External links
2632:
2631:
2630:
2623:
2616:
2611:Dale Rolfsen:
2607:
2604:
2601:
2600:
2597:
2594:
2591:
2588:
2585:
2582:
2581:4-genus (top.)
2578:
2577:
2574:
2571:
2568:
2565:
2562:
2559:
2555:
2554:
2543:
2540:
2537:
2527:
2514:
2510:
2499:
2486:
2482:
2471:
2458:
2454:
2443:
2430:
2426:
2415:
2402:
2398:
2387:
2358:
2355:
2343:Morse position
2326:
2323:
2320:
2317:
2291:
2287:
2266:
2263:
2260:
2257:
2254:
2251:
2246:
2242:
2221:
2218:
2215:
2212:
2209:
2206:
2201:
2197:
2176:
2173:
2170:
2167:
2164:
2161:
2156:
2152:
2148:
2145:
2123:
2119:
2096:
2092:
2070:
2067:
2054:
2051:
2048:
2045:
2042:
2039:
2016:
2013:
2002:
2001:
1989:
1986:
1981:
1977:
1973:
1970:
1965:
1961:
1957:
1952:
1948:
1944:
1939:
1935:
1912:
1908:
1904:
1901:
1896:
1892:
1861:
1857:
1842:
1830:
1827:
1824:
1804:
1757:
1754:
1751:
1748:
1745:
1742:
1722:
1699:
1694:
1691:
1687:
1683:
1680:
1677:
1674:
1671:
1668:
1665:
1662:
1659:
1656:
1653:
1637:
1634:
1619:
1615:
1611:
1606:
1602:
1579:
1575:
1571:
1566:
1562:
1539:
1535:
1531:
1528:
1523:
1519:
1515:
1510:
1506:
1485:
1482:
1479:
1476:
1456:
1453:
1450:
1447:
1444:
1441:
1438:
1416:
1412:
1401:Stevedore knot
1370:
1366:
1343:
1339:
1316:
1312:
1289:
1285:
1262:
1258:
1235:
1231:
1208:
1204:
1181:
1177:
1154:
1150:
1127:
1123:
1100:
1096:
1073:
1069:
1046:
1042:
1019:
1015:
992:
988:
965:
961:
938:
934:
911:
907:
884:
880:
857:
853:
830:
826:
805:
802:
799:
796:
793:
790:
787:
758:
755:
732:
728:
705:
701:
678:
674:
651:
647:
624:
620:
597:
593:
572:
552:
549:
546:
543:
521:
517:
503:we denote the
490:
486:
482:
460:
456:
452:
449:
444:
440:
410:
406:
402:
397:
393:
380:
377:
356:
353:
332:
329:
326:
323:
319:
314:
309:
305:
300:
295:
290:
286:
282:
279:
274:
270:
242:
239:
236:
232:
227:
222:
218:
213:
208:
203:
199:
195:
192:
187:
183:
157:
153:
149:
146:
141:
137:
106:
102:
67:
63:
59:
56:
44:
41:
25:Morse position
15:
9:
6:
4:
3:
2:
3518:
3507:
3504:
3503:
3501:
3486:
3485:
3476:
3474:
3473:
3464:
3463:
3460:
3454:
3451:
3449:
3446:
3444:
3441:
3439:
3436:
3434:
3431:
3429:
3426:
3424:
3421:
3419:
3416:
3414:
3411:
3409:
3406:
3404:
3401:
3399:
3396:
3394:
3391:
3389:
3388:Conway sphere
3386:
3384:
3381:
3379:
3376:
3374:
3371:
3370:
3368:
3364:
3358:
3355:
3353:
3350:
3348:
3345:
3343:
3340:
3338:
3335:
3333:
3330:
3328:
3325:
3323:
3320:
3319:
3317:
3315:
3308:
3302:
3298:
3295:
3293:
3290:
3288:
3285:
3281:
3278:
3277:
3276:
3273:
3271:
3268:
3264:
3261:
3259:
3256:
3254:
3251:
3249:
3246:
3244:
3241:
3240:
3239:
3236:
3234:
3231:
3229:
3226:
3224:
3221:
3219:
3216:
3214:
3211:
3209:
3206:
3204:
3201:
3199:
3196:
3194:
3191:
3187:
3184:
3183:
3182:
3179:
3177:
3174:
3170:
3167:
3166:
3165:
3162:
3160:
3159:Arf invariant
3157:
3155:
3152:
3151:
3149:
3147:
3143:
3127:
3124:
3112:
3109:
3097:
3094:
3087:
3084:
3077:
3074:
3067:
3064:
3057:
3054:
3053:
3051:
3049:
3045:
3039:
3036:
3032:
3029:
3027:
3024:
3023:
3022:
3019:
3018:
3016:
3014:
3010:
3004:
3001:
2989:
2986:
2974:
2971:
2968:
2965:
2962:
2959:
2956:
2953:
2946:
2943:
2936:
2933:
2926:
2923:
2921:
2915:
2913:
2907:
2900:
2897:
2890:
2887:
2880:
2877:
2876:
2874:
2872:
2868:
2863:
2859:
2855:
2848:
2843:
2841:
2836:
2834:
2829:
2828:
2825:
2816:
2815:
2808:
2801:
2795:
2788:
2785:
2779:
2772:
2766:
2759:
2755:
2751:
2746:
2737:
2730:
2724:
2717:
2713:
2709:
2708:Andrew Casson
2704:
2697:
2693:
2688:
2681:
2677:
2671:
2667:
2657:
2654:
2653:
2645:
2641:
2638:
2637:
2628:
2624:
2621:
2617:
2614:
2610:
2609:
2598:
2595:
2592:
2589:
2586:
2583:
2580:
2579:
2575:
2572:
2569:
2566:
2563:
2560:
2557:
2556:
2541:
2538:
2535:
2528:
2512:
2508:
2500:
2484:
2480:
2472:
2456:
2452:
2444:
2428:
2424:
2416:
2400:
2396:
2388:
2386:
2385:
2382:
2380:
2374:
2372:
2368:
2364:
2354:
2350:
2346:
2344:
2338:
2324:
2321:
2315:
2307:
2289:
2285:
2261:
2258:
2255:
2249:
2244:
2240:
2216:
2213:
2210:
2204:
2199:
2195:
2171:
2168:
2165:
2159:
2154:
2150:
2146:
2143:
2121:
2117:
2094:
2090:
2075:
2066:
2052:
2049:
2043:
2028:
2014:
2011:
1987:
1984:
1979:
1975:
1971:
1963:
1959:
1955:
1950:
1946:
1937:
1933:
1910:
1906:
1902:
1899:
1894:
1890:
1881:
1877:
1859:
1855:
1847:
1843:
1828:
1825:
1822:
1802:
1794:
1790:
1786:
1785:
1784:
1782:
1778:
1774:
1769:
1752:
1749:
1740:
1720:
1713:
1692:
1689:
1685:
1678:
1672:
1666:
1663:
1657:
1643:
1633:
1617:
1613:
1604:
1600:
1577:
1573:
1564:
1560:
1537:
1533:
1529:
1521:
1517:
1508:
1504:
1483:
1480:
1474:
1454:
1451:
1445:
1439:
1436:
1414:
1410:
1402:
1398:
1394:
1390:
1387:(named after
1386:
1368:
1364:
1341:
1337:
1314:
1310:
1287:
1283:
1260:
1256:
1233:
1229:
1206:
1202:
1179:
1175:
1152:
1148:
1125:
1121:
1098:
1094:
1071:
1067:
1044:
1040:
1017:
1013:
990:
986:
963:
959:
936:
932:
909:
905:
882:
878:
855:
851:
828:
824:
803:
800:
794:
788:
785:
777:
772:
763:
754:
752:
751:abelian group
748:
730:
726:
703:
699:
676:
672:
649:
645:
622:
618:
595:
591:
570:
550:
547:
541:
519:
515:
506:
488:
484:
480:
458:
454:
450:
442:
438:
430:
429:connected sum
426:
408:
404:
400:
395:
391:
376:
372:
370:
361:
352:
350:
345:
330:
324:
321:
303:
298:
288:
277:
272:
268:
260:
256:
237:
234:
216:
211:
201:
190:
185:
181:
173:
155:
151:
144:
139:
135:
126:
122:
104:
100:
91:
87:
83:
65:
61:
57:
54:
40:
38:
34:
26:
21:
3482:
3470:
3422:
3398:Double torus
3383:Braid theory
3198:Crossing no.
3193:Crosscap no.
2879:Figure-eight
2813:
2807:
2799:
2794:
2783:
2778:
2770:
2765:
2757:
2745:
2736:
2728:
2723:
2715:
2703:
2695:
2687:
2675:
2670:
2626:
2619:
2612:
2606:Bibliography
2378:
2375:
2360:
2351:
2347:
2339:
2306:orientations
2081:
2029:
2003:
1876:amphicheiral
1815:trefoils is
1793:trefoil knot
1777:homomorphism
1770:
1639:
816:. These are
773:
769:
505:mirror image
424:
382:
373:
366:
349:ribbon knots
346:
121:locally flat
85:
81:
46:
32:
30:
3233:Linking no.
3154:Alternating
2955:Conway knot
2935:Carrick mat
2889:Three-twist
2854:Knot theory
2754:John Milnor
2620:Knot theory
2379:alternating
1397:Twist knots
1385:Conway knot
776:prime knots
119:, which is
3393:Complement
3357:Tabulation
3314:operations
3238:Polynomial
3228:Link group
3223:Knot group
3186:Invertible
3164:Bridge no.
3146:Invariants
3076:Cinquefoil
2945:Perko pair
2871:Hyperbolic
2789:, p. 373).
2663:References
1880:invertible
1636:Invariants
425:concordant
43:Definition
33:slice knot
3287:Stick no.
3243:Alexander
3181:Chirality
3126:Solomon's
3086:Septafoil
3013:Satellite
2973:Whitehead
2899:Stevedore
2750:Ralph Fox
2322:−
2319:♯
2250:×
2205:×
2160:×
2038:Δ
1972:−
1969:♯
1943:♯
1903:−
1823:±
1773:signature
1750:−
1744:Δ
1690:−
1652:Δ
1610:♯
1570:♯
1530:−
1527:♯
1514:♯
1481:−
1478:♯
1452:≤
801:≤
548:−
545:♯
481:−
451:−
448:♯
427:, if the
322:≤
289:∈
202:∈
148:∂
58:⊂
3500:Category
3472:Category
3342:Mutation
3310:Notation
3263:Kauffman
3176:Brunnian
3169:2-bridge
3038:Knot sum
2969:(12n242)
2650:See also
2277:are two
1781:integers
757:Examples
255:boundary
172:3-sphere
90:embedded
3484:Commons
3403:Fibered
3301:problem
3270:Pretzel
3248:Bracket
3066:Trefoil
3003:L10a140
2963:(11n42)
2957:(11n34)
2925:Endless
2367:4-genus
2357:4-genus
2027:exist.
1710:with a
253:is the
47:A knot
3448:Writhe
3418:Ribbon
3253:HOMFLY
3096:Unlink
3056:Unknot
3031:Square
3026:Granny
2365:. The
1393:mutant
170:: the
125:smooth
3438:Twist
3423:Slice
3378:Berge
3366:Other
3337:Flype
3275:Prime
3258:Jones
3218:Genus
3048:Torus
2862:links
2858:knots
2371:genus
2363:genus
1789:order
691:then
84:or a
35:is a
3443:Wild
3408:Knot
3312:and
3299:and
3280:list
3111:Hopf
2860:and
2109:and
2012:>
1878:and
1771:The
1592:and
1496:and
1356:and
637:and
369:cone
259:ball
3428:Sum
2949:161
2947:(10
2513:161
2485:154
2457:152
2429:145
2401:139
1874:is
1369:155
1342:153
1315:140
1288:137
1261:129
1234:123
507:of
123:or
3502::
3128:(4
3113:(2
3098:(0
3088:(7
3078:(5
3068:(3
3058:(0
2990:(6
2975:(5
2939:18
2937:(8
2927:(7
2901:(6
2891:(5
2881:(4
2756::
2752:,
2714::
2710:,
2694::
2678:,
2642::
2599:0
2576:1
2542:34
2536:11
2509:10
2481:10
2453:10
2425:10
2397:10
2345:.
1632:.
1618:11
1578:10
1455:12
1365:10
1338:10
1329:,
1311:10
1302:,
1284:10
1275:,
1257:10
1248:,
1230:10
1221:,
1207:99
1203:10
1194:,
1180:87
1176:10
1167:,
1153:75
1149:10
1140:,
1126:48
1122:10
1113:,
1099:42
1095:10
1086:,
1072:35
1068:10
1059:,
1045:22
1041:10
1032:,
1014:10
1005:,
991:46
978:,
964:41
951:,
937:27
924:,
910:20
897:,
870:,
843:,
804:10
31:A
3137:)
3133:1
3122:)
3118:1
3107:)
3103:1
3092:)
3090:1
3082:)
3080:1
3072:)
3070:1
3062:)
3060:1
2999:)
2995:2
2984:)
2980:1
2951:)
2941:)
2931:)
2929:4
2919:3
2917:6
2911:2
2909:6
2905:)
2903:1
2895:)
2893:2
2885:)
2883:1
2864:)
2856:(
2846:e
2839:t
2832:v
2596:2
2593:2
2590:3
2587:1
2584:3
2573:3
2570:3
2567:4
2564:2
2561:4
2539:n
2325:K
2316:K
2290:3
2286:S
2265:]
2262:1
2259:,
2256:0
2253:[
2245:3
2241:S
2220:]
2217:1
2214:,
2211:0
2208:[
2200:3
2196:S
2175:]
2172:1
2169:,
2166:0
2163:[
2155:1
2151:S
2147:=
2144:C
2122:2
2118:K
2095:1
2091:K
2053:1
2050:=
2047:)
2044:t
2041:(
2015:2
1988:0
1985:=
1980:1
1976:4
1964:1
1960:4
1956:=
1951:1
1947:4
1938:1
1934:4
1911:1
1907:4
1900:=
1895:1
1891:4
1860:1
1856:4
1829:n
1826:2
1803:n
1756:)
1753:1
1747:(
1741:=
1721:f
1698:)
1693:1
1686:t
1682:(
1679:f
1676:)
1673:t
1670:(
1667:f
1664:=
1661:)
1658:t
1655:(
1614:8
1605:1
1601:3
1574:8
1565:1
1561:3
1538:1
1534:3
1522:1
1518:3
1509:1
1505:6
1484:K
1475:K
1449:)
1446:K
1443:(
1440:r
1437:c
1415:1
1411:6
1018:3
987:9
960:9
933:9
906:8
883:9
879:8
856:8
852:8
829:1
825:6
798:)
795:K
792:(
789:r
786:c
731:3
727:K
704:1
700:K
677:3
673:K
650:2
646:K
623:2
619:K
596:1
592:K
571:K
551:K
542:K
520:2
516:K
489:2
485:K
459:2
455:K
443:1
439:K
409:2
405:K
401:,
396:1
392:K
331:.
328:}
325:1
318:|
313:x
308:|
304::
299:4
294:R
285:x
281:{
278:=
273:4
269:B
241:}
238:1
235:=
231:|
226:x
221:|
217::
212:4
207:R
198:x
194:{
191:=
186:3
182:S
156:4
152:B
145:=
140:3
136:S
105:4
101:B
66:3
62:S
55:K
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.