564:
31:
146:
In a weighted, undirected network, it is possible to calculate the cut that separates a particular pair of vertices from each other and has minimum possible weight. A system of cuts that solves this problem for every possible vertex pair can be collected into a structure known as the
139:, the minimum cut separates the source and sink vertices and minimizes the total sum of the capacities of the edges that are directed from the source side of the cut to the sink side of the cut. As shown in the
203:
problems are a family of combinatorial optimization problems in which a graph is to be partitioned into two or more parts with additional constraints such as balancing the sizes of the two sides of the cut.
34:
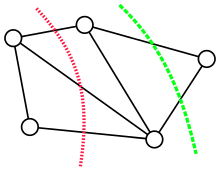
A graph and two of its cuts. The dotted line in red represents a cut with three crossing edges. The dashed line in green represents one of the minimum cuts of this graph, crossing only two edges.
356:
424:
248:
190:
380:
287:
517:
461:
65:
Variations of the minimum cut problem consider weighted graphs, directed graphs, terminals, and partitioning the vertices into more than two sets.
205:
143:, the weight of this cut equals the maximum amount of flow that can be sent from the source to the sink in the given network.
292:
489:
68:
The weighted min-cut problem allowing both positive and negative weights can be trivially transformed into a weighted
224:
and edge weights are their distances. This is however often impractical due do the high computational complexity for
548:
465:
606:
601:
579:
572:
51:
596:
385:
261:
value. In this case, some algorithms used in maxflow problem could also be used to solve this question.
359:
92:
provides an efficient randomized method for finding the cut. In this case, the minimum cut equals the
582:
incorrectly led you here, you may wish to change the link to point directly to the intended article.
254:
140:
115:, this problem can be solved in polynomial time, though the algorithm is not practical for large
17:
93:
85:
484:
89:
227:
516:
Dahlhaus, E.; Johnson, D. S.; Papadimitriou, C. H.; Seymour, P. D.; Yannakakis, M. (1994).
84:, weighted graphs limited to non-negative weights can be solved in polynomial time by the
8:
209:
169:
540:
365:
272:
213:
148:
59:
55:
62:
of the vertices of a graph into two disjoint subsets) that is minimal in some metric.
480:
162:, this problem can be solved in polynomial time. However, in general this problem is
544:
532:
498:
440:
217:
81:
200:
111:
connected components by removing as few edges as possible. For a fixed value of
575:
includes a list of related items that share the same name (or similar names).
536:
590:
100:
221:
159:
136:
39:
502:
435:
163:
127:
When two terminal nodes are given, they are typically referred to as the
69:
99:
A generalization of the minimum cut problem without terminals is the
443:, an analogous concept to minimum cuts for vertices instead of edges
220:
method, where the nodes are data samples assumed to be taken from a
515:
154:
A generalization of the minimum cut problem with terminals is the
30:
258:
563:
358:
distinct minimum cuts. This bound is tight in the sense that a
107:, in which the goal is to partition the graph into at least
485:"A Polynomial Algorithm for the k-cut Problem for Fixed k"
208:
can be viewed as a specific case of normalized min-cut
27:
Partition of a graph by removing fewest possible edges
388:
368:
295:
275:
230:
172:
88:. In the special case when the graph is unweighted,
478:
351:{\displaystyle {\binom {n}{2}}={\frac {n(n-1)}{2}}}
418:
374:
350:
281:
242:
184:
312:
299:
588:
569:Index of articles associated with the same name
257:, 2 nodes' Minimum cut value is equal to their
72:problem by flipping the sign in all weights.
561:
158:-terminal cut, or multi-terminal cut. In a
264:
75:
206:Segmentation-based object categorization
29:
14:
589:
518:"The Complexity of Multiterminal Cuts"
122:
419:{\displaystyle {\frac {n(n-1)}{2}}}
216:. It can also be used as a generic
24:
490:Mathematics of Operations Research
303:
25:
618:
562:
195:
509:
472:
454:
407:
395:
339:
327:
289:vertices can at the most have
13:
1:
447:
7:
429:
80:The minimum cut problem in
10:
623:
537:10.1137/S0097539792225297
525:SIAM Journal on Computing
255:max-flow min-cut theorem
141:max-flow min-cut theorem
479:Goldschmidt, Olivier;
462:"4 Min-Cut Algorithms"
420:
376:
352:
283:
265:Number of minimum cuts
244:
243:{\displaystyle k>2}
186:
86:Stoer-Wagner algorithm
76:Without terminal nodes
35:
421:
382:vertices has exactly
377:
353:
284:
245:
187:
33:
607:Network flow problem
602:Graph theory objects
503:10.1287/moor.19.1.24
386:
366:
293:
273:
228:
170:
210:spectral clustering
185:{\displaystyle k=3}
123:With terminal nodes
597:Set index articles
481:Hochbaum, Dorit S.
416:
372:
348:
279:
240:
214:image segmentation
182:
90:Karger's algorithm
36:
573:set index article
414:
375:{\displaystyle n}
346:
310:
282:{\displaystyle n}
94:edge connectivity
16:(Redirected from
614:
583:
566:
556:
555:
553:
547:. Archived from
522:
513:
507:
506:
476:
470:
469:
464:. Archived from
458:
441:Vertex separator
425:
423:
422:
417:
415:
410:
390:
381:
379:
378:
373:
357:
355:
354:
349:
347:
342:
322:
317:
316:
315:
302:
288:
286:
285:
280:
249:
247:
246:
241:
191:
189:
188:
183:
157:
118:
114:
110:
104:
21:
622:
621:
617:
616:
615:
613:
612:
611:
587:
586:
585:
584:
577:
576:
570:
560:
559:
551:
520:
514:
510:
477:
473:
460:
459:
455:
450:
432:
391:
389:
387:
384:
383:
367:
364:
363:
323:
321:
311:
298:
297:
296:
294:
291:
290:
274:
271:
270:
267:
229:
226:
225:
201:Graph partition
198:
171:
168:
167:
155:
125:
116:
112:
108:
102:
78:
28:
23:
22:
15:
12:
11:
5:
620:
610:
609:
604:
599:
568:
567:
558:
557:
554:on 2018-12-25.
531:(4): 864–894.
508:
471:
468:on 2016-08-05.
452:
451:
449:
446:
445:
444:
438:
431:
428:
426:minimum cuts.
413:
409:
406:
403:
400:
397:
394:
371:
360:(simple) cycle
345:
341:
338:
335:
332:
329:
326:
320:
314:
309:
306:
301:
278:
266:
263:
239:
236:
233:
197:
194:
181:
178:
175:
151:of the graph.
149:Gomory–Hu tree
124:
121:
96:of the graph.
77:
74:
26:
9:
6:
4:
3:
2:
619:
608:
605:
603:
600:
598:
595:
594:
592:
581:
580:internal link
574:
565:
550:
546:
542:
538:
534:
530:
526:
519:
512:
504:
500:
496:
492:
491:
486:
482:
475:
467:
463:
457:
453:
442:
439:
437:
434:
433:
427:
411:
404:
401:
398:
392:
369:
361:
343:
336:
333:
330:
324:
318:
307:
304:
276:
269:A graph with
262:
260:
256:
251:
237:
234:
231:
223:
219:
215:
211:
207:
202:
193:
179:
176:
173:
165:
161:
152:
150:
144:
142:
138:
134:
130:
120:
106:
97:
95:
91:
87:
83:
73:
71:
66:
63:
61:
57:
53:
49:
45:
41:
32:
19:
549:the original
528:
524:
511:
494:
488:
474:
466:the original
456:
268:
252:
222:metric space
199:
196:Applications
160:planar graph
153:
145:
137:flow network
132:
128:
126:
98:
79:
67:
64:
47:
43:
40:graph theory
37:
436:Maximum cut
212:applied to
166:, even for
70:maximum cut
44:minimum cut
591:Categories
448:References
218:clustering
82:undirected
497:: 24–37.
402:−
334:−
60:partition
483:(1994).
430:See also
131:and the
101:minimum
545:1123876
259:maxflow
253:Due to
164:NP-hard
135:. In a
48:min-cut
18:Min-cut
578:If an
543:
129:source
571:This
552:(PDF)
541:S2CID
521:(PDF)
54:is a
52:graph
50:of a
235:>
133:sink
105:-cut
42:, a
533:doi
499:doi
362:on
119:.
58:(a
56:cut
46:or
38:In
593::
539:.
529:23
527:.
523:.
495:19
493:.
487:.
250:.
192:.
535::
505:.
501::
412:2
408:)
405:1
399:n
396:(
393:n
370:n
344:2
340:)
337:1
331:n
328:(
325:n
319:=
313:)
308:2
305:n
300:(
277:n
238:2
232:k
180:3
177:=
174:k
156:k
117:k
113:k
109:k
103:k
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.