57:
5418:
5954:
5231:
5794:
1074:
5196:
4665:
3024:
4530:
4808:
2740:
4260:
3357:
5413:{\displaystyle {\begin{matrix}{\textbf {Hom}}(L,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(L,Y)\\i^{*}\downarrow &&\downarrow i^{*}\\{\textbf {Hom}}(K,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(K,Y)\end{matrix}}}
5949:{\displaystyle \pi _{n}(X,x)=\left\{\alpha :\Delta ^{n}\to X:{\begin{matrix}\Delta ^{n}&{\overset {\alpha }{\to }}&X\\\uparrow &&\uparrow x\\\partial \Delta ^{n}&\to &\Delta ^{0}\end{matrix}}\right\}}
4401:
4079:
3751:
with an infinity groupoid. It is conjectured that the homotopy category of geometric realizations of infinity groupoids is equivalent to the homotopy category of homotopy types. This is called the homotopy hypothesis.
206:
5629:
5552:
2188:
3973:
6158:
3553:
6689:
5053:
840:
4546:
3616:
4946:
3253:
2134:
467:
4029:
2090:
2274:
6206:
3877:
1217:
6332:
3498:
3441:
2015:
2820:
2568:
1257:
4719:
6283:
4449:
4016:
1413:
2487:
910:
5786:
1625:
4877:
620:
5648:
of a fibrant simplicial set may be defined combinatorially, using horns, in a way that agrees with the homotopy groups of the topological space which realizes it. For a Kan complex
6059:
5987:
5045:
4163:
2828:
324:
6760:
6501:
5705:
2400:
1773:
272:
1295:
1574:
1347:
1111:
1036:
526:
378:
5223:
3725:
712:
4457:
3749:
3652:
6374:
5747:
3157:
3124:
3087:
1173:
4307:
6436:
4973:
3832:
3805:
2042:
1374:
1063:
553:
494:
409:
117:
6789:
6721:
6558:
1937:
1477:
1445:
968:
5013:
4727:
6400:
1141:
2576:
936:
6238:
6014:
5475:
5448:
1967:
1004:
744:
674:
4171:
3186:
4121:
3054:
3264:
1734:
1671:
1648:
6598:
6578:
6529:
5666:
3778:
2423:
2358:
2338:
2318:
2298:
2208:
1901:
1873:
1853:
1833:
1813:
1793:
1711:
1691:
1541:
1521:
1315:
643:
573:
235:
88:
6462:
3698:
335:
4315:
4024:
6334:
gives their addition. This map is well-defined up to simplicial homotopy classes of maps, giving the group structure. Moreover, the groups
125:
5557:
5480:
2142:
5191:{\displaystyle {\textbf {Hom}}(L,X)\xrightarrow {(i^{*},p_{*})} {\textbf {Hom}}(K,X)\times _{{\textbf {Hom}}(K,Y)}{\textbf {Hom}}(L,Y)}
3885:
6067:
3503:
6606:
4660:{\displaystyle {\text{ev}}_{*}:{\text{Hom}}_{s{\text{Sets}}}(K,{\textbf {Hom}}(X,Y))\to {\text{Hom}}_{s{\text{Sets}}}(X\times K,Y)}
2210:
is a Kan complex. Conversely, every Kan complex has this property, hence it gives a simple technical condition for a Kan complex.
3807:
is not a Kan complex. The construction of a counter example in general can be found by looking at a low dimensional example, say
749:
3558:
69:
6985:
6900:
4882:
3209:
2098:
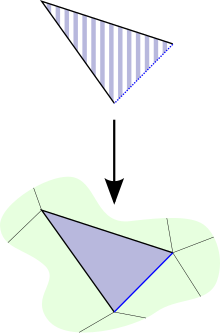
1815:. The diagram to the right is an example in two dimensions. Since the black V in the lower diagram is filled in by the blue
426:
2047:
2240:
7019:
6166:
3837:
1178:
6288:
3453:
3381:
1976:
3618:
are correspond to Kan complexes of some simplicial set. In fact, this set can be constructed explicitly using the
2748:
2496:
1222:
4673:
6243:
4409:
3981:
1379:
6822:
2431:
848:
419:-th face removed. This may be formally defined in various ways, as for instance the union of the images of the
5752:
1583:
4816:
3201:
3019:{\displaystyle (s_{i}f)(t_{0},\dots ,t_{n+1})=f(t_{0},\dots ,t_{i-1},t_{i}+t_{i+1},t_{i+2},\dots ,t_{n+1})\,}
581:
6838:
6019:
5962:
5018:
4129:
277:
7011:
3619:
6726:
6467:
5671:
2366:
2224:
1739:
242:
6817:
4525:{\displaystyle X\times \Delta ^{m}\xrightarrow {1\times \theta } X\times \Delta ^{n}\xrightarrow {f} Y}
1262:
1546:
1320:
1084:
1009:
499:
351:
5204:
3703:
1492:
679:
212:
3730:
3633:
7051:
7046:
6337:
5710:
5225:
is in the function complex in the category of simplicial sets) induced from the commutative diagram
3372:
3129:
3096:
3059:
1146:
4268:
6405:
4951:
4803:{\displaystyle X\times K\xrightarrow {1\times g} X\times {\textbf {Hom}}(X,Y)\xrightarrow {ev} Y}
3810:
3783:
2020:
1352:
1041:
531:
472:
387:
95:
6765:
6697:
6534:
5477:
is the pushforward map given by post-composition. In particular, the previous fibration implies
1910:
1450:
1418:
35:
structure on simplicial sets and are therefore of fundamental importance. Kan complexes are the
2735:{\displaystyle (d_{i}f)(t_{0},\dots ,t_{n-1})=f(t_{0},\dots ,t_{i-1},0,t_{i},\dots ,t_{n-1})\,}
941:
60:
The striped blue simplex in the domain has to exist in order for this map to be a Kan fibration
4986:
6796:
6379:
4255:{\displaystyle {\textbf {Hom}}_{n}(X,Y)={\text{Hom}}_{s{\text{Sets}}}(X\times \Delta ^{n},Y)}
3622:
of a chain complex and taking the underlying simplicial set of the simplicial abelian group.
1120:
3630:
Another important source of examples are the simplicial sets associated to a small groupoid
915:
7029:
6995:
6792:
6211:
5992:
5453:
5426:
3375:, its geometric realization is homotopy equivalent to a product of Eilenberg-Maclane spaces
3352:{\displaystyle {\text{Hom}}_{\text{Top}}(|X|,Y)\cong {\text{Hom}}_{s{\text{Sets}}}(X,S(Y))}
1946:
977:
717:
647:
6933:
Friedman, Greg (2016-10-03). "An elementary illustrated introduction to simplicial sets".
3162:
8:
4100:
3090:
3033:
1716:
1653:
1630:
6934:
6583:
6563:
6514:
5651:
4018:
because the maps have to be order preserving. If there was a map, it would have to send
3763:
2408:
2343:
2323:
2303:
2283:
2193:
1886:
1858:
1838:
1818:
1798:
1778:
1696:
1676:
1526:
1506:
1300:
628:
558:
220:
73:
6441:
6163:
Defining the group structure requires a little more work. Essentially, given two maps
3657:
216:
7015:
6981:
6906:
6896:
3447:
2228:
6973:
6827:
3368:
3197:
7025:
6991:
6800:
4396:{\displaystyle \theta ^{*}:{\textbf {Hom}}(X,Y)_{n}\to {\textbf {Hom}}(X,Y)_{m}}
4074:{\displaystyle {\begin{aligned}0\mapsto 0\\1\mapsto 1\\2\mapsto 0\end{aligned}}}
6833:
6812:
5645:
1970:
1940:
36:
32:
28:
6977:
1580:), this definition can be written in terms of simplices. The image of the map
7040:
6910:
7003:
6965:
6951:
1577:
6580:
in the homotopy category of simplicial sets. Then, the homotopy groups of
4406:(since the first factor of Hom is contravariant) defined by sending a map
6791:. These fibrant replacements can be thought of a topological analogue of
40:
6890:
3654:. This is defined as the geometric realization of the simplicial set
1969:
is the terminal object and so a Kan complex is exactly the same as a
1835:-simplex, if the black V above maps down to it then the striped blue
1484:
201:{\displaystyle \Delta ^{n}(i)=\mathrm {Hom} _{\mathbf {\Delta } }(,)}
5369:
5267:
5083:
4788:
4744:
4513:
4481:
3126:, any continuous function defined on these faces can be extended to
5989:
is mapped to a point is equivalent to the definition of the sphere
2320:-simplex of X to be a continuous map from the standard topological
1488:
6939:
5624:{\displaystyle i^{*}:{\textbf {Hom}}(L,Y)\to {\textbf {Hom}}(K,Y)}
5547:{\displaystyle p_{*}:{\textbf {Hom}}(L,X)\to {\textbf {Hom}}(L,Y)}
2183:{\displaystyle \iota :\Lambda _{k}^{n}\hookrightarrow \Delta ^{n}}
714:. Explicitly, this condition can be written as follows. Write the
4540:
This complex has the following exponential law of simplicial sets
3968:{\displaystyle {\begin{matrix}\mapsto &\mapsto \end{matrix}}}
215:
functor to this simplicial set gives a space homeomorphic to the
56:
6153:{\displaystyle B^{n}=\{x\in \mathbb {R} ^{n}:||x||_{eu}\leq 1\}}
1073:
5788:
of simplicial sets fitting into a certain commutative diagram:
4092:
3548:{\displaystyle \mathbb {CP} ^{\infty }\simeq K(\mathbb {Z} ,2)}
3362:
6684:{\displaystyle \pi _{n}(X,x):=\pi _{n}({\hat {X}},{\hat {x}})}
676:-simplices satisfying a compatibility condition, one for each
3978:
gives a counter example since it cannot be extended to a map
3625:
1878:
1627:
can be thought of as a horn as described above. Asking that
1939:, the one-point simplicial set, is a Kan fibration. In the
835:{\displaystyle (s_{0},\dots ,s_{k-1},s_{k+1},\dots ,s_{n})}
555:
look like the black V at the top of the adjacent image. If
6952:
An elementary illustrated introduction to simplicial sets
3611:{\displaystyle L_{q}^{\infty }\simeq K(\mathbb {Z} /q,2)}
2218:
326:
such that the coordinates are non-negative and sum to 1.
4941:{\displaystyle \iota _{n}\in {\text{Hom}}_{\Delta }(,)}
3248:{\displaystyle |\cdot |:s{\text{Sets}}\to {\text{Top}}}
51:
5857:
5236:
3890:
3191:
2129:{\displaystyle \alpha ={\tilde {\alpha }}\circ \iota }
1973:. Equivalently, this could be stated as: if every map
1736:(together with one other face). Then the required map
6768:
6729:
6700:
6609:
6586:
6566:
6537:
6517:
6506:
6470:
6444:
6408:
6382:
6340:
6291:
6246:
6214:
6169:
6070:
6022:
5995:
5965:
5797:
5755:
5713:
5674:
5654:
5560:
5483:
5456:
5429:
5234:
5207:
5056:
5021:
4989:
4954:
4885:
4819:
4730:
4676:
4549:
4460:
4412:
4318:
4271:
4174:
4132:
4103:
4027:
3984:
3888:
3840:
3813:
3786:
3766:
3733:
3706:
3660:
3636:
3561:
3506:
3456:
3384:
3367:
It can be shown that the simplicial set underlying a
3267:
3212:
3165:
3132:
3099:
3062:
3036:
2831:
2751:
2579:
2499:
2493:
To make this into a simplicial set, define face maps
2434:
2411:
2369:
2346:
2326:
2306:
2286:
2243:
2196:
2145:
2101:
2050:
2023:
1979:
1949:
1913:
1889:
1861:
1841:
1821:
1801:
1781:
1742:
1719:
1699:
1679:
1656:
1633:
1586:
1549:
1529:
1509:
1453:
1421:
1382:
1355:
1323:
1303:
1265:
1225:
1181:
1149:
1123:
1087:
1044:
1012:
980:
944:
918:
851:
752:
720:
682:
650:
631:
584:
561:
534:
502:
475:
429:
390:
354:
280:
245:
223:
128:
98:
76:
2223:
An important example comes from the construction of
462:{\displaystyle \Delta ^{n-1}\rightarrow \Delta ^{n}}
31:. Kan fibrations are the fibrations of the standard
5639:
2085:{\displaystyle {\tilde {\alpha }}:\Delta ^{n}\to X}
6783:
6754:
6715:
6683:
6592:
6572:
6552:
6523:
6495:
6456:
6430:
6394:
6368:
6326:
6277:
6232:
6200:
6152:
6053:
6008:
5981:
5948:
5780:
5741:
5699:
5660:
5623:
5546:
5469:
5450:is the pull-back map given by pre-composiiton and
5442:
5412:
5217:
5190:
5039:
5007:
4967:
4940:
4871:
4802:
4713:
4659:
4524:
4443:
4395:
4301:
4254:
4157:
4115:
4073:
4010:
3967:
3871:
3826:
3799:
3772:
3755:
3743:
3719:
3692:
3646:
3610:
3547:
3492:
3435:
3351:
3247:
3180:
3151:
3118:
3081:
3048:
3018:
2814:
2734:
2562:
2481:
2417:
2405:Taking the set of these maps for all non-negative
2394:
2352:
2332:
2312:
2292:
2268:
2202:
2182:
2128:
2084:
2036:
2009:
1961:
1931:
1895:
1867:
1855:-simplex has to exist, along with the dotted blue
1847:
1827:
1807:
1787:
1767:
1728:
1705:
1685:
1665:
1642:
1619:
1568:
1535:
1515:
1471:
1439:
1407:
1368:
1341:
1309:
1289:
1251:
1211:
1167:
1135:
1105:
1057:
1030:
998:
962:
930:
904:
834:
738:
706:
668:
637:
614:
567:
547:
520:
488:
461:
403:
372:
318:
266:
229:
200:
111:
82:
4123:there is an associated simplicial set called the
16:Map between simplicial sets with lifting property
7038:
7010:. Chicago Lectures in Mathematics. Chicago, IL:
6874:May uses this simplicial definition; see page 25
4978:
2269:{\displaystyle S:{\text{Top}}\to s{\text{Sets}}}
1068:
39:in this model category. The name is in honor of
6201:{\displaystyle \alpha ,\beta :\Delta ^{n}\to X}
3872:{\displaystyle \Lambda _{0}^{2}\to \Delta ^{1}}
1212:{\displaystyle s:\Lambda _{k}^{n}\rightarrow X}
6830:(also called quasi-category, ∞-category)
6963:
6327:{\displaystyle d_{n}\omega :\Delta ^{n}\to X}
3493:{\displaystyle S^{1}\simeq K(\mathbb {Z} ,1)}
3436:{\displaystyle \prod _{i\in I}K(A_{i},n_{i})}
2010:{\displaystyle \alpha :\Lambda _{k}^{n}\to X}
6888:
6147:
6084:
4093:Simplicial enrichment and function complexes
3363:Simplicial sets underlying simplicial groups
2815:{\displaystyle s_{i}:S_{n}(X)\to S_{n+1}(X)}
2563:{\displaystyle d_{i}:S_{n}(X)\to S_{n-1}(X)}
1956:
1950:
1926:
1920:
1252:{\displaystyle y:\Delta ^{n}\rightarrow Y\,}
6511:Using model categories, any simplicial set
4714:{\displaystyle f:K\to {\textbf {Hom}}(X,Y)}
3196:It is worth noting the singular functor is
1875:-simplex, mapping down in the obvious way.
6278:{\displaystyle \omega :\Delta ^{n+1}\to X}
4444:{\displaystyle f:X\times \Delta ^{n}\to Y}
4011:{\displaystyle \Delta ^{2}\to \Delta ^{1}}
1673:corresponds to requiring that there is an
1408:{\displaystyle x:\Delta ^{n}\rightarrow X}
6938:
6889:Goerss, Paul G.; Jardin, John F. (2009).
6095:
4087:
4084:but this isn't a map of simplicial sets.
3626:Geometric realizations of small groupoids
3587:
3532:
3512:
3509:
3477:
3015:
2731:
2482:{\displaystyle S(X)=\coprod _{n}S_{n}(X)}
1879:Kan complexes defined from Kan fibrations
1248:
905:{\displaystyle d_{i}s_{j}=d_{j-1}s_{i}\,}
901:
248:
7008:Simplicial objects in algebraic topology
6932:
6438:, it is defined as the homotopy classes
5781:{\displaystyle \alpha :\Delta ^{n}\to X}
3371:is always fibrant. In particular, for a
1620:{\displaystyle fs:\Lambda _{k}^{n}\to Y}
1072:
469:corresponding to all the other faces of
55:
4872:{\displaystyle ev(x,f)=f(x,\iota _{n})}
974:These conditions are satisfied for the
615:{\displaystyle s:\Lambda _{k}^{n}\to X}
411:, corresponding to the boundary of the
329:
7039:
2219:Simplicial sets from singular homology
119:, is the representable simplicial set
1479:. Stated this way, the definition is
6884:
6882:
6880:
6054:{\displaystyle B^{n}/\partial B^{n}}
5982:{\displaystyle \partial \Delta ^{n}}
5040:{\displaystyle i:K\hookrightarrow L}
5015:and an inclusion of simplicial sets
4165:, where the simplices are defined as
4158:{\displaystyle {\textbf {Hom}}(X,Y)}
1498:
319:{\displaystyle (t_{0},\dots ,t_{n})}
52:Definition of the standard n-simplex
7002:
5601:
5576:
5524:
5499:
5386:
5343:
5284:
5241:
5210:
5168:
5144:
5117:
5059:
4764:
4691:
4593:
4366:
4334:
4178:
4135:
3192:Relation with geometric realization
1077:Lifting diagram for a Kan fibration
13:
6755:{\displaystyle x:\Delta ^{0}\to X}
6737:
6507:Homotopy groups of simplicial sets
6496:{\displaystyle x:\Delta ^{0}\to X}
6478:
6309:
6254:
6183:
6038:
5970:
5966:
5928:
5911:
5907:
5861:
5838:
5763:
5700:{\displaystyle x:\Delta ^{0}\to X}
5682:
4956:
4906:
4535:
4500:
4468:
4426:
4234:
3999:
3986:
3860:
3842:
3815:
3788:
3736:
3712:
3682:
3665:
3639:
3572:
3517:
3134:
3101:
3064:
2395:{\displaystyle f:\Delta _{n}\to X}
2377:
2171:
2153:
2067:
2025:
1987:
1795:whose faces include the horn from
1768:{\displaystyle x:\Delta ^{n}\to X}
1750:
1713:whose faces make up the horn from
1597:
1551:
1390:
1357:
1325:
1233:
1189:
1046:
1014:
592:
536:
504:
477:
450:
431:
392:
356:
267:{\displaystyle \mathbb {R} ^{n+1}}
159:
156:
153:
130:
100:
14:
7063:
6877:
2340:-simplex (as described above) to
1503:Using the correspondence between
1290:{\displaystyle f\circ s=y\circ i}
6560:which is homotopy equivalent to
5640:Homotopy groups of Kan complexes
2017:from a horn has an extension to
1569:{\displaystyle \Delta ^{n}\to X}
1495:), whence the name "fibration".
1342:{\displaystyle \Lambda _{k}^{n}}
1106:{\displaystyle f:X\rightarrow Y}
1031:{\displaystyle \Lambda _{k}^{n}}
521:{\displaystyle \Lambda _{k}^{2}}
373:{\displaystyle \Lambda _{k}^{n}}
165:
68: ≥ 0, recall that the
6957:
5634:
5218:{\displaystyle {\textbf {Hom}}}
3756:Non-example: standard n-simplex
3720:{\displaystyle B{\mathcal {G}}}
3555:, and the infinite lens spaces
1523:-simplices of a simplicial set
707:{\displaystyle 0\leq k\leq n-1}
575:is a simplicial set, then maps
6926:
6917:
6868:
6859:
6856:See Goerss and Jardine, page 7
6850:
6823:Simplicially enriched category
6793:resolutions of a chain complex
6775:
6746:
6707:
6678:
6672:
6657:
6648:
6632:
6620:
6544:
6487:
6451:
6445:
6425:
6419:
6363:
6351:
6318:
6269:
6227:
6215:
6192:
6128:
6122:
6114:
6109:
5922:
5897:
5891:
5874:
5847:
5820:
5808:
5772:
5749:is defined as the set of maps
5736:
5724:
5691:
5618:
5606:
5596:
5593:
5581:
5541:
5529:
5519:
5516:
5504:
5403:
5391:
5360:
5348:
5324:
5318:
5301:
5289:
5258:
5246:
5185:
5173:
5161:
5149:
5134:
5122:
5110:
5084:
5076:
5064:
5031:
4999:
4935:
4932:
4926:
4920:
4914:
4911:
4866:
4847:
4838:
4826:
4781:
4769:
4708:
4696:
4686:
4654:
4636:
4616:
4613:
4610:
4598:
4582:
4435:
4384:
4371:
4361:
4352:
4339:
4296:
4290:
4287:
4284:
4278:
4249:
4224:
4201:
4189:
4152:
4140:
4061:
4048:
4035:
3995:
3958:
3946:
3943:
3940:
3928:
3923:
3911:
3908:
3905:
3893:
3856:
3744:{\displaystyle {\mathcal {G}}}
3727:. We could have also replaced
3687:
3661:
3647:{\displaystyle {\mathcal {G}}}
3605:
3583:
3542:
3528:
3487:
3473:
3430:
3404:
3346:
3343:
3337:
3325:
3302:
3292:
3284:
3280:
3237:
3222:
3214:
3175:
3169:
3012:
2898:
2889:
2851:
2848:
2832:
2809:
2803:
2784:
2781:
2775:
2728:
2646:
2637:
2599:
2596:
2580:
2557:
2551:
2532:
2529:
2523:
2476:
2470:
2444:
2438:
2386:
2255:
2167:
2114:
2076:
2057:
2001:
1917:
1759:
1611:
1560:
1399:
1242:
1203:
1097:
993:
981:
829:
753:
733:
721:
663:
651:
606:
446:
313:
281:
195:
192:
186:
180:
174:
171:
145:
139:
46:
1:
6844:
6369:{\displaystyle \pi _{n}(X,x)}
5742:{\displaystyle \pi _{n}(X,x)}
4979:Kan fibrations and pull-backs
3446:In particular, this includes
3202:geometric realization functor
3152:{\displaystyle \Delta _{n+1}}
3119:{\displaystyle \Delta _{n+1}}
3082:{\displaystyle \Delta _{n+1}}
1168:{\displaystyle 0\leq k\leq n}
1069:Definition of a Kan fibration
625:correspond to collections of
6839:Fibration of simplicial sets
4302:{\displaystyle \theta :\to }
1775:corresponds to a simplex in
7:
7012:University of Chicago Press
6972:. Basel: Birkhäuser Basel.
6806:
6431:{\displaystyle \pi _{0}(X)}
4968:{\displaystyle \Delta ^{n}}
3827:{\displaystyle \Delta ^{1}}
3800:{\displaystyle \Delta ^{n}}
2213:
2037:{\displaystyle \Delta ^{n}}
1369:{\displaystyle \Delta ^{n}}
1058:{\displaystyle \Delta ^{n}}
548:{\displaystyle \Delta ^{2}}
489:{\displaystyle \Delta ^{n}}
404:{\displaystyle \Delta ^{n}}
112:{\displaystyle \Delta ^{n}}
10:
7068:
6970:Simplicial Homotopy Theory
6892:Simplicial Homotopy Theory
6818:Simplicial homotopy theory
6784:{\displaystyle {\hat {X}}}
6716:{\displaystyle {\hat {x}}}
6553:{\displaystyle {\hat {X}}}
6531:has a fibrant replacement
6061:for the standard unit ball
3760:It turns out the standard
2044:, meaning there is a lift
1932:{\displaystyle X\to \{*\}}
1472:{\displaystyle y=f\circ x}
1440:{\displaystyle s=x\circ i}
333:
27:are part of the theory of
6978:10.1007/978-3-0348-8707-6
3700:and is typically denoted
1493:homotopy lifting property
1081:A map of simplicial sets
963:{\displaystyle i,j\neq k}
274:consisting of all points
239:: the convex subspace of
5008:{\displaystyle p:X\to Y}
4983:Given a (Kan) fibration
4948:lifted to the n-simplex
3373:simplicial abelian group
348:, this has a subcomplex
6395:{\displaystyle n\geq 2}
6208:there is an associated
5047:, there is a fibration
4309:there is an induced map
4265:and for an ordinal map
3620:Dold–Kan correspondence
3030:Since the union of any
1136:{\displaystyle n\geq 1}
6785:
6756:
6717:
6692:
6685:
6594:
6574:
6554:
6525:
6497:
6458:
6432:
6396:
6370:
6328:
6279:
6234:
6202:
6161:
6154:
6055:
6010:
5983:
5957:
5950:
5782:
5743:
5701:
5662:
5625:
5548:
5471:
5444:
5421:
5414:
5219:
5199:
5192:
5041:
5009:
4969:
4942:
4873:
4811:
4804:
4715:
4668:
4661:
4533:
4526:
4445:
4404:
4397:
4303:
4263:
4256:
4159:
4117:
4088:Categorical properties
4082:
4075:
4012:
3976:
3969:
3873:
3828:
3801:
3774:
3745:
3721:
3694:
3648:
3612:
3549:
3494:
3444:
3437:
3360:
3353:
3258:giving the isomorphism
3256:
3249:
3182:
3153:
3120:
3083:
3050:
3020:
2816:
2736:
2564:
2483:
2419:
2396:
2354:
2334:
2314:
2294:
2278:
2270:
2204:
2184:
2139:for the inclusion map
2137:
2130:
2086:
2038:
2011:
1963:
1933:
1897:
1869:
1849:
1829:
1809:
1789:
1769:
1730:
1707:
1687:
1667:
1644:
1621:
1576:(a consequence of the
1570:
1537:
1517:
1473:
1441:
1409:
1376:), there exists a map
1370:
1343:
1311:
1291:
1253:
1213:
1169:
1137:
1107:
1078:
1059:
1032:
1000:
964:
932:
931:{\displaystyle i<j}
906:
836:
740:
708:
670:
639:
616:
569:
549:
522:
490:
463:
405:
374:
320:
268:
231:
202:
113:
84:
61:
6797:projective resolution
6786:
6757:
6718:
6686:
6602:
6595:
6575:
6555:
6526:
6498:
6459:
6433:
6397:
6371:
6329:
6280:
6235:
6233:{\displaystyle (n+1)}
6203:
6155:
6063:
6056:
6011:
6009:{\displaystyle S^{n}}
5984:
5951:
5790:
5783:
5744:
5702:
5663:
5626:
5549:
5472:
5470:{\displaystyle p_{*}}
5445:
5443:{\displaystyle i^{*}}
5415:
5227:
5220:
5193:
5049:
5042:
5010:
4970:
4943:
4874:
4805:
4723:
4716:
4662:
4542:
4527:
4453:
4446:
4398:
4311:
4304:
4257:
4167:
4160:
4118:
4076:
4020:
4013:
3970:
3881:
3874:
3829:
3802:
3775:
3746:
3722:
3695:
3649:
3613:
3550:
3495:
3438:
3377:
3354:
3260:
3250:
3205:
3183:
3154:
3121:
3084:
3051:
3021:
2817:
2737:
2565:
2484:
2420:
2397:
2355:
2335:
2315:
2295:
2271:
2236:
2205:
2185:
2131:
2094:
2087:
2039:
2012:
1964:
1962:{\displaystyle \{*\}}
1943:for simplicial sets,
1934:
1898:
1870:
1850:
1830:
1810:
1790:
1770:
1731:
1708:
1688:
1668:
1645:
1622:
1571:
1538:
1518:
1474:
1442:
1410:
1371:
1344:
1312:
1292:
1254:
1214:
1170:
1138:
1108:
1076:
1060:
1033:
1001:
999:{\displaystyle (n-1)}
965:
933:
907:
837:
746:-simplices as a list
741:
739:{\displaystyle (n-1)}
709:
671:
669:{\displaystyle (n-1)}
640:
617:
570:
550:
523:
491:
464:
406:
375:
321:
269:
232:
217:topological standard
213:geometric realization
203:
114:
85:
59:
6895:. Birkhäuser Basel.
6766:
6727:
6698:
6607:
6584:
6564:
6535:
6515:
6468:
6442:
6406:
6380:
6338:
6289:
6244:
6212:
6167:
6068:
6020:
5993:
5963:
5795:
5753:
5711:
5672:
5652:
5558:
5481:
5454:
5427:
5232:
5205:
5054:
5019:
4987:
4952:
4883:
4817:
4728:
4721:to the composite map
4674:
4547:
4458:
4410:
4316:
4269:
4172:
4130:
4101:
4097:For simplicial sets
4025:
3982:
3886:
3838:
3811:
3784:
3764:
3731:
3704:
3658:
3634:
3559:
3504:
3454:
3382:
3265:
3210:
3181:{\displaystyle S(X)}
3163:
3130:
3097:
3060:
3034:
2829:
2749:
2745:and degeneracy maps
2577:
2497:
2432:
2425:gives a graded set,
2409:
2367:
2344:
2324:
2304:
2300:, define a singular
2284:
2241:
2194:
2143:
2099:
2048:
2021:
1977:
1947:
1911:
1887:
1859:
1839:
1819:
1799:
1779:
1740:
1717:
1697:
1677:
1654:
1631:
1584:
1547:
1527:
1507:
1451:
1419:
1380:
1353:
1321:
1317:is the inclusion of
1301:
1263:
1223:
1179:
1147:
1121:
1085:
1042:
1010:
978:
942:
916:
849:
750:
718:
680:
648:
629:
582:
559:
532:
500:
496:. Horns of the form
473:
427:
388:
352:
330:Definition of a horn
278:
243:
221:
126:
96:
74:
5380:
5278:
5113:
4795:
4754:
4517:
4491:
4116:{\displaystyle X,Y}
3855:
3576:
3159:, which shows that
3091:deformation retract
3049:{\displaystyle n+1}
2166:
2000:
1610:
1338:
1202:
1175:, and for any maps
1027:
605:
517:
415:-simplex, with the
369:
6781:
6752:
6713:
6681:
6590:
6570:
6550:
6521:
6493:
6454:
6428:
6392:
6366:
6324:
6275:
6230:
6198:
6150:
6051:
6006:
5979:
5946:
5939:
5778:
5739:
5697:
5658:
5621:
5544:
5467:
5440:
5410:
5408:
5215:
5188:
5037:
5005:
4965:
4938:
4869:
4800:
4711:
4670:which sends a map
4657:
4522:
4451:to the composition
4441:
4393:
4299:
4252:
4155:
4113:
4071:
4069:
4008:
3965:
3963:
3869:
3841:
3824:
3797:
3770:
3741:
3717:
3690:
3644:
3608:
3562:
3545:
3490:
3448:classifying spaces
3433:
3400:
3349:
3245:
3188:is a Kan complex.
3178:
3149:
3116:
3079:
3046:
3016:
2812:
2732:
2560:
2479:
2459:
2415:
2392:
2350:
2330:
2310:
2290:
2266:
2225:singular simplices
2200:
2180:
2152:
2126:
2082:
2034:
2007:
1986:
1959:
1929:
1893:
1865:
1845:
1825:
1805:
1785:
1765:
1729:{\displaystyle fs}
1726:
1703:
1683:
1666:{\displaystyle yi}
1663:
1643:{\displaystyle fs}
1640:
1617:
1596:
1566:
1533:
1513:
1469:
1437:
1405:
1366:
1339:
1324:
1307:
1287:
1249:
1209:
1188:
1165:
1133:
1103:
1079:
1055:
1028:
1013:
996:
960:
928:
902:
832:
736:
704:
666:
635:
612:
591:
565:
545:
518:
503:
486:
459:
401:
370:
355:
316:
264:
227:
198:
109:
80:
62:
6987:978-3-0348-9737-2
6964:Goerss, Paul G.;
6902:978-3-0346-0188-7
6778:
6710:
6675:
6660:
6600:can be defined as
6593:{\displaystyle X}
6573:{\displaystyle X}
6547:
6524:{\displaystyle X}
5880:
5661:{\displaystyle X}
5603:
5578:
5526:
5501:
5388:
5381:
5345:
5286:
5279:
5243:
5212:
5170:
5146:
5119:
5114:
5061:
4903:
4796:
4766:
4755:
4693:
4632:
4623:
4595:
4578:
4569:
4554:
4518:
4492:
4368:
4336:
4220:
4211:
4180:
4137:
3834:. Taking the map
3773:{\displaystyle n}
3385:
3321:
3312:
3277:
3272:
3243:
3235:
2450:
2418:{\displaystyle n}
2353:{\displaystyle X}
2333:{\displaystyle n}
2313:{\displaystyle n}
2293:{\displaystyle X}
2264:
2253:
2229:singular homology
2203:{\displaystyle X}
2117:
2060:
1896:{\displaystyle X}
1883:A simplicial set
1868:{\displaystyle 1}
1848:{\displaystyle 2}
1828:{\displaystyle 2}
1808:{\displaystyle s}
1788:{\displaystyle X}
1706:{\displaystyle Y}
1686:{\displaystyle n}
1536:{\displaystyle X}
1516:{\displaystyle n}
1499:Technical remarks
1310:{\displaystyle i}
842:and require that
638:{\displaystyle n}
568:{\displaystyle X}
336:Horn of a simplex
230:{\displaystyle n}
83:{\displaystyle n}
7059:
7033:
6999:
6966:Jardine, John F.
6945:
6944:
6942:
6930:
6924:
6921:
6915:
6914:
6886:
6875:
6872:
6866:
6863:
6857:
6854:
6828:Weak Kan complex
6790:
6788:
6787:
6782:
6780:
6779:
6771:
6761:
6759:
6758:
6753:
6745:
6744:
6722:
6720:
6719:
6714:
6712:
6711:
6703:
6690:
6688:
6687:
6682:
6677:
6676:
6668:
6662:
6661:
6653:
6647:
6646:
6619:
6618:
6599:
6597:
6596:
6591:
6579:
6577:
6576:
6571:
6559:
6557:
6556:
6551:
6549:
6548:
6540:
6530:
6528:
6527:
6522:
6502:
6500:
6499:
6494:
6486:
6485:
6463:
6461:
6460:
6457:{\displaystyle }
6455:
6437:
6435:
6434:
6429:
6418:
6417:
6401:
6399:
6398:
6393:
6376:are Abelian for
6375:
6373:
6372:
6367:
6350:
6349:
6333:
6331:
6330:
6325:
6317:
6316:
6301:
6300:
6284:
6282:
6281:
6276:
6268:
6267:
6239:
6237:
6236:
6231:
6207:
6205:
6204:
6199:
6191:
6190:
6159:
6157:
6156:
6151:
6140:
6139:
6131:
6125:
6117:
6112:
6104:
6103:
6098:
6080:
6079:
6060:
6058:
6057:
6052:
6050:
6049:
6037:
6032:
6031:
6016:as the quotient
6015:
6013:
6012:
6007:
6005:
6004:
5988:
5986:
5985:
5980:
5978:
5977:
5959:Notice the fact
5955:
5953:
5952:
5947:
5945:
5941:
5940:
5936:
5935:
5919:
5918:
5895:
5881:
5873:
5869:
5868:
5846:
5845:
5807:
5806:
5787:
5785:
5784:
5779:
5771:
5770:
5748:
5746:
5745:
5740:
5723:
5722:
5706:
5704:
5703:
5698:
5690:
5689:
5667:
5665:
5664:
5659:
5631:are fibrations.
5630:
5628:
5627:
5622:
5605:
5604:
5580:
5579:
5570:
5569:
5553:
5551:
5550:
5545:
5528:
5527:
5503:
5502:
5493:
5492:
5476:
5474:
5473:
5468:
5466:
5465:
5449:
5447:
5446:
5441:
5439:
5438:
5419:
5417:
5416:
5411:
5409:
5390:
5389:
5379:
5378:
5365:
5347:
5346:
5336:
5335:
5322:
5317:
5316:
5288:
5287:
5277:
5276:
5263:
5245:
5244:
5224:
5222:
5221:
5216:
5214:
5213:
5197:
5195:
5194:
5189:
5172:
5171:
5165:
5164:
5148:
5147:
5121:
5120:
5109:
5108:
5096:
5095:
5079:
5063:
5062:
5046:
5044:
5043:
5038:
5014:
5012:
5011:
5006:
4974:
4972:
4971:
4966:
4964:
4963:
4947:
4945:
4944:
4939:
4910:
4909:
4904:
4901:
4895:
4894:
4878:
4876:
4875:
4870:
4865:
4864:
4809:
4807:
4806:
4801:
4784:
4768:
4767:
4740:
4720:
4718:
4717:
4712:
4695:
4694:
4666:
4664:
4663:
4658:
4635:
4634:
4633:
4630:
4624:
4621:
4597:
4596:
4581:
4580:
4579:
4576:
4570:
4567:
4561:
4560:
4555:
4552:
4531:
4529:
4528:
4523:
4509:
4508:
4507:
4477:
4476:
4475:
4450:
4448:
4447:
4442:
4434:
4433:
4402:
4400:
4399:
4394:
4392:
4391:
4370:
4369:
4360:
4359:
4338:
4337:
4328:
4327:
4308:
4306:
4305:
4300:
4261:
4259:
4258:
4253:
4242:
4241:
4223:
4222:
4221:
4218:
4212:
4209:
4188:
4187:
4182:
4181:
4164:
4162:
4161:
4156:
4139:
4138:
4125:function complex
4122:
4120:
4119:
4114:
4080:
4078:
4077:
4072:
4070:
4017:
4015:
4014:
4009:
4007:
4006:
3994:
3993:
3974:
3972:
3971:
3966:
3964:
3878:
3876:
3875:
3870:
3868:
3867:
3854:
3849:
3833:
3831:
3830:
3825:
3823:
3822:
3806:
3804:
3803:
3798:
3796:
3795:
3779:
3777:
3776:
3771:
3750:
3748:
3747:
3742:
3740:
3739:
3726:
3724:
3723:
3718:
3716:
3715:
3699:
3697:
3696:
3693:{\displaystyle }
3691:
3686:
3685:
3676:
3675:
3653:
3651:
3650:
3645:
3643:
3642:
3617:
3615:
3614:
3609:
3595:
3590:
3575:
3570:
3554:
3552:
3551:
3546:
3535:
3521:
3520:
3515:
3499:
3497:
3496:
3491:
3480:
3466:
3465:
3450:. So the spaces
3442:
3440:
3439:
3434:
3429:
3428:
3416:
3415:
3399:
3369:simplicial group
3358:
3356:
3355:
3350:
3324:
3323:
3322:
3319:
3313:
3310:
3295:
3287:
3279:
3278:
3275:
3273:
3270:
3254:
3252:
3251:
3246:
3244:
3241:
3236:
3233:
3225:
3217:
3187:
3185:
3184:
3179:
3158:
3156:
3155:
3150:
3148:
3147:
3125:
3123:
3122:
3117:
3115:
3114:
3088:
3086:
3085:
3080:
3078:
3077:
3055:
3053:
3052:
3047:
3025:
3023:
3022:
3017:
3011:
3010:
2986:
2985:
2967:
2966:
2948:
2947:
2935:
2934:
2910:
2909:
2888:
2887:
2863:
2862:
2844:
2843:
2821:
2819:
2818:
2813:
2802:
2801:
2774:
2773:
2761:
2760:
2741:
2739:
2738:
2733:
2727:
2726:
2702:
2701:
2683:
2682:
2658:
2657:
2636:
2635:
2611:
2610:
2592:
2591:
2569:
2567:
2566:
2561:
2550:
2549:
2522:
2521:
2509:
2508:
2488:
2486:
2485:
2480:
2469:
2468:
2458:
2424:
2422:
2421:
2416:
2401:
2399:
2398:
2393:
2385:
2384:
2359:
2357:
2356:
2351:
2339:
2337:
2336:
2331:
2319:
2317:
2316:
2311:
2299:
2297:
2296:
2291:
2275:
2273:
2272:
2267:
2265:
2262:
2254:
2251:
2233:singular functor
2209:
2207:
2206:
2201:
2189:
2187:
2186:
2181:
2179:
2178:
2165:
2160:
2135:
2133:
2132:
2127:
2119:
2118:
2110:
2091:
2089:
2088:
2083:
2075:
2074:
2062:
2061:
2053:
2043:
2041:
2040:
2035:
2033:
2032:
2016:
2014:
2013:
2008:
1999:
1994:
1968:
1966:
1965:
1960:
1938:
1936:
1935:
1930:
1907:if the map from
1902:
1900:
1899:
1894:
1874:
1872:
1871:
1866:
1854:
1852:
1851:
1846:
1834:
1832:
1831:
1826:
1814:
1812:
1811:
1806:
1794:
1792:
1791:
1786:
1774:
1772:
1771:
1766:
1758:
1757:
1735:
1733:
1732:
1727:
1712:
1710:
1709:
1704:
1692:
1690:
1689:
1684:
1672:
1670:
1669:
1664:
1650:factors through
1649:
1647:
1646:
1641:
1626:
1624:
1623:
1618:
1609:
1604:
1575:
1573:
1572:
1567:
1559:
1558:
1542:
1540:
1539:
1534:
1522:
1520:
1519:
1514:
1478:
1476:
1475:
1470:
1446:
1444:
1443:
1438:
1414:
1412:
1411:
1406:
1398:
1397:
1375:
1373:
1372:
1367:
1365:
1364:
1348:
1346:
1345:
1340:
1337:
1332:
1316:
1314:
1313:
1308:
1296:
1294:
1293:
1288:
1258:
1256:
1255:
1250:
1241:
1240:
1218:
1216:
1215:
1210:
1201:
1196:
1174:
1172:
1171:
1166:
1142:
1140:
1139:
1134:
1112:
1110:
1109:
1104:
1064:
1062:
1061:
1056:
1054:
1053:
1037:
1035:
1034:
1029:
1026:
1021:
1005:
1003:
1002:
997:
969:
967:
966:
961:
937:
935:
934:
929:
911:
909:
908:
903:
900:
899:
890:
889:
871:
870:
861:
860:
841:
839:
838:
833:
828:
827:
809:
808:
790:
789:
765:
764:
745:
743:
742:
737:
713:
711:
710:
705:
675:
673:
672:
667:
644:
642:
641:
636:
621:
619:
618:
613:
604:
599:
574:
572:
571:
566:
554:
552:
551:
546:
544:
543:
527:
525:
524:
519:
516:
511:
495:
493:
492:
487:
485:
484:
468:
466:
465:
460:
458:
457:
445:
444:
410:
408:
407:
402:
400:
399:
384:-th horn inside
379:
377:
376:
371:
368:
363:
325:
323:
322:
317:
312:
311:
293:
292:
273:
271:
270:
265:
263:
262:
251:
236:
234:
233:
228:
207:
205:
204:
199:
170:
169:
168:
162:
138:
137:
118:
116:
115:
110:
108:
107:
89:
87:
86:
81:
19:In mathematics,
7067:
7066:
7062:
7061:
7060:
7058:
7057:
7056:
7052:Homotopy theory
7047:Simplicial sets
7037:
7036:
7022:
6988:
6960:
6948:
6931:
6927:
6923:See May, page 3
6922:
6918:
6903:
6887:
6878:
6873:
6869:
6865:See May, page 2
6864:
6860:
6855:
6851:
6847:
6809:
6801:flat resolution
6770:
6769:
6767:
6764:
6763:
6740:
6736:
6728:
6725:
6724:
6702:
6701:
6699:
6696:
6695:
6667:
6666:
6652:
6651:
6642:
6638:
6614:
6610:
6608:
6605:
6604:
6585:
6582:
6581:
6565:
6562:
6561:
6539:
6538:
6536:
6533:
6532:
6516:
6513:
6512:
6509:
6481:
6477:
6469:
6466:
6465:
6464:of vertex maps
6443:
6440:
6439:
6413:
6409:
6407:
6404:
6403:
6381:
6378:
6377:
6345:
6341:
6339:
6336:
6335:
6312:
6308:
6296:
6292:
6290:
6287:
6286:
6257:
6253:
6245:
6242:
6241:
6213:
6210:
6209:
6186:
6182:
6168:
6165:
6164:
6132:
6127:
6126:
6121:
6113:
6108:
6099:
6094:
6093:
6075:
6071:
6069:
6066:
6065:
6045:
6041:
6033:
6027:
6023:
6021:
6018:
6017:
6000:
5996:
5994:
5991:
5990:
5973:
5969:
5964:
5961:
5960:
5938:
5937:
5931:
5927:
5925:
5920:
5914:
5910:
5904:
5903:
5894:
5888:
5887:
5882:
5872:
5870:
5864:
5860:
5856:
5841:
5837:
5830:
5826:
5802:
5798:
5796:
5793:
5792:
5766:
5762:
5754:
5751:
5750:
5718:
5714:
5712:
5709:
5708:
5685:
5681:
5673:
5670:
5669:
5653:
5650:
5649:
5646:homotopy groups
5642:
5637:
5600:
5599:
5575:
5574:
5565:
5561:
5559:
5556:
5555:
5523:
5522:
5498:
5497:
5488:
5484:
5482:
5479:
5478:
5461:
5457:
5455:
5452:
5451:
5434:
5430:
5428:
5425:
5424:
5407:
5406:
5385:
5384:
5382:
5374:
5370:
5363:
5342:
5341:
5338:
5337:
5331:
5327:
5321:
5312:
5308:
5305:
5304:
5283:
5282:
5280:
5272:
5268:
5261:
5240:
5239:
5235:
5233:
5230:
5229:
5209:
5208:
5206:
5203:
5202:
5167:
5166:
5143:
5142:
5141:
5137:
5116:
5115:
5104:
5100:
5091:
5087:
5058:
5057:
5055:
5052:
5051:
5020:
5017:
5016:
4988:
4985:
4984:
4981:
4959:
4955:
4953:
4950:
4949:
4905:
4900:
4899:
4890:
4886:
4884:
4881:
4880:
4860:
4856:
4818:
4815:
4814:
4763:
4762:
4729:
4726:
4725:
4690:
4689:
4675:
4672:
4671:
4629:
4625:
4620:
4619:
4592:
4591:
4575:
4571:
4566:
4565:
4556:
4551:
4550:
4548:
4545:
4544:
4538:
4536:Exponential law
4503:
4499:
4471:
4467:
4459:
4456:
4455:
4429:
4425:
4411:
4408:
4407:
4387:
4383:
4365:
4364:
4355:
4351:
4333:
4332:
4323:
4319:
4317:
4314:
4313:
4270:
4267:
4266:
4237:
4233:
4217:
4213:
4208:
4207:
4183:
4177:
4176:
4175:
4173:
4170:
4169:
4134:
4133:
4131:
4128:
4127:
4102:
4099:
4098:
4095:
4090:
4068:
4067:
4055:
4054:
4042:
4041:
4028:
4026:
4023:
4022:
4002:
3998:
3989:
3985:
3983:
3980:
3979:
3962:
3961:
3926:
3889:
3887:
3884:
3883:
3863:
3859:
3850:
3845:
3839:
3836:
3835:
3818:
3814:
3812:
3809:
3808:
3791:
3787:
3785:
3782:
3781:
3765:
3762:
3761:
3758:
3735:
3734:
3732:
3729:
3728:
3711:
3710:
3705:
3702:
3701:
3681:
3680:
3668:
3664:
3659:
3656:
3655:
3638:
3637:
3635:
3632:
3631:
3628:
3591:
3586:
3571:
3566:
3560:
3557:
3556:
3531:
3516:
3508:
3507:
3505:
3502:
3501:
3476:
3461:
3457:
3455:
3452:
3451:
3424:
3420:
3411:
3407:
3389:
3383:
3380:
3379:
3365:
3318:
3314:
3309:
3308:
3291:
3283:
3274:
3269:
3268:
3266:
3263:
3262:
3240:
3232:
3221:
3213:
3211:
3208:
3207:
3194:
3164:
3161:
3160:
3137:
3133:
3131:
3128:
3127:
3104:
3100:
3098:
3095:
3094:
3067:
3063:
3061:
3058:
3057:
3035:
3032:
3031:
3000:
2996:
2975:
2971:
2956:
2952:
2943:
2939:
2924:
2920:
2905:
2901:
2877:
2873:
2858:
2854:
2839:
2835:
2830:
2827:
2826:
2791:
2787:
2769:
2765:
2756:
2752:
2750:
2747:
2746:
2716:
2712:
2697:
2693:
2672:
2668:
2653:
2649:
2625:
2621:
2606:
2602:
2587:
2583:
2578:
2575:
2574:
2539:
2535:
2517:
2513:
2504:
2500:
2498:
2495:
2494:
2464:
2460:
2454:
2433:
2430:
2429:
2410:
2407:
2406:
2380:
2376:
2368:
2365:
2364:
2345:
2342:
2341:
2325:
2322:
2321:
2305:
2302:
2301:
2285:
2282:
2281:
2261:
2250:
2242:
2239:
2238:
2227:used to define
2221:
2216:
2195:
2192:
2191:
2174:
2170:
2161:
2156:
2144:
2141:
2140:
2109:
2108:
2100:
2097:
2096:
2070:
2066:
2052:
2051:
2049:
2046:
2045:
2028:
2024:
2022:
2019:
2018:
1995:
1990:
1978:
1975:
1974:
1948:
1945:
1944:
1912:
1909:
1908:
1888:
1885:
1884:
1881:
1860:
1857:
1856:
1840:
1837:
1836:
1820:
1817:
1816:
1800:
1797:
1796:
1780:
1777:
1776:
1753:
1749:
1741:
1738:
1737:
1718:
1715:
1714:
1698:
1695:
1694:
1678:
1675:
1674:
1655:
1652:
1651:
1632:
1629:
1628:
1605:
1600:
1585:
1582:
1581:
1554:
1550:
1548:
1545:
1544:
1528:
1525:
1524:
1508:
1505:
1504:
1501:
1452:
1449:
1448:
1420:
1417:
1416:
1393:
1389:
1381:
1378:
1377:
1360:
1356:
1354:
1351:
1350:
1333:
1328:
1322:
1319:
1318:
1302:
1299:
1298:
1264:
1261:
1260:
1236:
1232:
1224:
1221:
1220:
1197:
1192:
1180:
1177:
1176:
1148:
1145:
1144:
1122:
1119:
1118:
1086:
1083:
1082:
1071:
1049:
1045:
1043:
1040:
1039:
1038:sitting inside
1022:
1017:
1011:
1008:
1007:
979:
976:
975:
943:
940:
939:
917:
914:
913:
895:
891:
879:
875:
866:
862:
856:
852:
850:
847:
846:
823:
819:
798:
794:
779:
775:
760:
756:
751:
748:
747:
719:
716:
715:
681:
678:
677:
649:
646:
645:
630:
627:
626:
600:
595:
583:
580:
579:
560:
557:
556:
539:
535:
533:
530:
529:
528:sitting inside
512:
507:
501:
498:
497:
480:
476:
474:
471:
470:
453:
449:
434:
430:
428:
425:
424:
395:
391:
389:
386:
385:
364:
359:
353:
350:
349:
338:
332:
307:
303:
288:
284:
279:
276:
275:
252:
247:
246:
244:
241:
240:
222:
219:
218:
164:
163:
152:
151:
133:
129:
127:
124:
123:
103:
99:
97:
94:
93:
75:
72:
71:
54:
49:
37:fibrant objects
29:simplicial sets
17:
12:
11:
5:
7065:
7055:
7054:
7049:
7035:
7034:
7020:
7000:
6986:
6959:
6956:
6955:
6954:
6947:
6946:
6925:
6916:
6901:
6876:
6867:
6858:
6848:
6846:
6843:
6842:
6841:
6836:
6831:
6825:
6820:
6815:
6813:Model category
6808:
6805:
6777:
6774:
6751:
6748:
6743:
6739:
6735:
6732:
6709:
6706:
6680:
6674:
6671:
6665:
6659:
6656:
6650:
6645:
6641:
6637:
6634:
6631:
6628:
6625:
6622:
6617:
6613:
6589:
6569:
6546:
6543:
6520:
6508:
6505:
6492:
6489:
6484:
6480:
6476:
6473:
6453:
6450:
6447:
6427:
6424:
6421:
6416:
6412:
6391:
6388:
6385:
6365:
6362:
6359:
6356:
6353:
6348:
6344:
6323:
6320:
6315:
6311:
6307:
6304:
6299:
6295:
6274:
6271:
6266:
6263:
6260:
6256:
6252:
6249:
6229:
6226:
6223:
6220:
6217:
6197:
6194:
6189:
6185:
6181:
6178:
6175:
6172:
6149:
6146:
6143:
6138:
6135:
6130:
6124:
6120:
6116:
6111:
6107:
6102:
6097:
6092:
6089:
6086:
6083:
6078:
6074:
6048:
6044:
6040:
6036:
6030:
6026:
6003:
5999:
5976:
5972:
5968:
5944:
5934:
5930:
5926:
5924:
5921:
5917:
5913:
5909:
5906:
5905:
5902:
5899:
5896:
5893:
5890:
5889:
5886:
5883:
5879:
5876:
5871:
5867:
5863:
5859:
5858:
5855:
5852:
5849:
5844:
5840:
5836:
5833:
5829:
5825:
5822:
5819:
5816:
5813:
5810:
5805:
5801:
5777:
5774:
5769:
5765:
5761:
5758:
5738:
5735:
5732:
5729:
5726:
5721:
5717:
5696:
5693:
5688:
5684:
5680:
5677:
5657:
5641:
5638:
5636:
5633:
5620:
5617:
5614:
5611:
5608:
5598:
5595:
5592:
5589:
5586:
5583:
5573:
5568:
5564:
5543:
5540:
5537:
5534:
5531:
5521:
5518:
5515:
5512:
5509:
5506:
5496:
5491:
5487:
5464:
5460:
5437:
5433:
5405:
5402:
5399:
5396:
5393:
5383:
5377:
5373:
5368:
5364:
5362:
5359:
5356:
5353:
5350:
5340:
5339:
5334:
5330:
5326:
5323:
5320:
5315:
5311:
5307:
5306:
5303:
5300:
5297:
5294:
5291:
5281:
5275:
5271:
5266:
5262:
5260:
5257:
5254:
5251:
5248:
5238:
5237:
5187:
5184:
5181:
5178:
5175:
5163:
5160:
5157:
5154:
5151:
5140:
5136:
5133:
5130:
5127:
5124:
5112:
5107:
5103:
5099:
5094:
5090:
5086:
5082:
5078:
5075:
5072:
5069:
5066:
5036:
5033:
5030:
5027:
5024:
5004:
5001:
4998:
4995:
4992:
4980:
4977:
4962:
4958:
4937:
4934:
4931:
4928:
4925:
4922:
4919:
4916:
4913:
4908:
4898:
4893:
4889:
4868:
4863:
4859:
4855:
4852:
4849:
4846:
4843:
4840:
4837:
4834:
4831:
4828:
4825:
4822:
4799:
4794:
4791:
4787:
4783:
4780:
4777:
4774:
4771:
4761:
4758:
4753:
4750:
4747:
4743:
4739:
4736:
4733:
4710:
4707:
4704:
4701:
4698:
4688:
4685:
4682:
4679:
4656:
4653:
4650:
4647:
4644:
4641:
4638:
4628:
4618:
4615:
4612:
4609:
4606:
4603:
4600:
4590:
4587:
4584:
4574:
4564:
4559:
4537:
4534:
4521:
4516:
4512:
4506:
4502:
4498:
4495:
4490:
4487:
4484:
4480:
4474:
4470:
4466:
4463:
4440:
4437:
4432:
4428:
4424:
4421:
4418:
4415:
4390:
4386:
4382:
4379:
4376:
4373:
4363:
4358:
4354:
4350:
4347:
4344:
4341:
4331:
4326:
4322:
4298:
4295:
4292:
4289:
4286:
4283:
4280:
4277:
4274:
4251:
4248:
4245:
4240:
4236:
4232:
4229:
4226:
4216:
4206:
4203:
4200:
4197:
4194:
4191:
4186:
4154:
4151:
4148:
4145:
4142:
4112:
4109:
4106:
4094:
4091:
4089:
4086:
4066:
4063:
4060:
4057:
4056:
4053:
4050:
4047:
4044:
4043:
4040:
4037:
4034:
4031:
4030:
4005:
4001:
3997:
3992:
3988:
3960:
3957:
3954:
3951:
3948:
3945:
3942:
3939:
3936:
3933:
3930:
3927:
3925:
3922:
3919:
3916:
3913:
3910:
3907:
3904:
3901:
3898:
3895:
3892:
3891:
3866:
3862:
3858:
3853:
3848:
3844:
3821:
3817:
3794:
3790:
3769:
3757:
3754:
3738:
3714:
3709:
3689:
3684:
3679:
3674:
3671:
3667:
3663:
3641:
3627:
3624:
3607:
3604:
3601:
3598:
3594:
3589:
3585:
3582:
3579:
3574:
3569:
3565:
3544:
3541:
3538:
3534:
3530:
3527:
3524:
3519:
3514:
3511:
3489:
3486:
3483:
3479:
3475:
3472:
3469:
3464:
3460:
3432:
3427:
3423:
3419:
3414:
3410:
3406:
3403:
3398:
3395:
3392:
3388:
3364:
3361:
3348:
3345:
3342:
3339:
3336:
3333:
3330:
3327:
3317:
3307:
3304:
3301:
3298:
3294:
3290:
3286:
3282:
3239:
3231:
3228:
3224:
3220:
3216:
3193:
3190:
3177:
3174:
3171:
3168:
3146:
3143:
3140:
3136:
3113:
3110:
3107:
3103:
3076:
3073:
3070:
3066:
3045:
3042:
3039:
3028:
3027:
3014:
3009:
3006:
3003:
2999:
2995:
2992:
2989:
2984:
2981:
2978:
2974:
2970:
2965:
2962:
2959:
2955:
2951:
2946:
2942:
2938:
2933:
2930:
2927:
2923:
2919:
2916:
2913:
2908:
2904:
2900:
2897:
2894:
2891:
2886:
2883:
2880:
2876:
2872:
2869:
2866:
2861:
2857:
2853:
2850:
2847:
2842:
2838:
2834:
2811:
2808:
2805:
2800:
2797:
2794:
2790:
2786:
2783:
2780:
2777:
2772:
2768:
2764:
2759:
2755:
2743:
2742:
2730:
2725:
2722:
2719:
2715:
2711:
2708:
2705:
2700:
2696:
2692:
2689:
2686:
2681:
2678:
2675:
2671:
2667:
2664:
2661:
2656:
2652:
2648:
2645:
2642:
2639:
2634:
2631:
2628:
2624:
2620:
2617:
2614:
2609:
2605:
2601:
2598:
2595:
2590:
2586:
2582:
2559:
2556:
2553:
2548:
2545:
2542:
2538:
2534:
2531:
2528:
2525:
2520:
2516:
2512:
2507:
2503:
2491:
2490:
2478:
2475:
2472:
2467:
2463:
2457:
2453:
2449:
2446:
2443:
2440:
2437:
2414:
2403:
2402:
2391:
2388:
2383:
2379:
2375:
2372:
2349:
2329:
2309:
2289:
2280:Given a space
2260:
2257:
2249:
2246:
2220:
2217:
2215:
2212:
2199:
2177:
2173:
2169:
2164:
2159:
2155:
2151:
2148:
2125:
2122:
2116:
2113:
2107:
2104:
2081:
2078:
2073:
2069:
2065:
2059:
2056:
2031:
2027:
2006:
2003:
1998:
1993:
1989:
1985:
1982:
1971:fibrant object
1958:
1955:
1952:
1941:model category
1928:
1925:
1922:
1919:
1916:
1892:
1880:
1877:
1864:
1844:
1824:
1804:
1784:
1764:
1761:
1756:
1752:
1748:
1745:
1725:
1722:
1702:
1682:
1662:
1659:
1639:
1636:
1616:
1613:
1608:
1603:
1599:
1595:
1592:
1589:
1565:
1562:
1557:
1553:
1543:and morphisms
1532:
1512:
1500:
1497:
1468:
1465:
1462:
1459:
1456:
1436:
1433:
1430:
1427:
1424:
1404:
1401:
1396:
1392:
1388:
1385:
1363:
1359:
1336:
1331:
1327:
1306:
1286:
1283:
1280:
1277:
1274:
1271:
1268:
1247:
1244:
1239:
1235:
1231:
1228:
1208:
1205:
1200:
1195:
1191:
1187:
1184:
1164:
1161:
1158:
1155:
1152:
1132:
1129:
1126:
1102:
1099:
1096:
1093:
1090:
1070:
1067:
1052:
1048:
1025:
1020:
1016:
1006:-simplices of
995:
992:
989:
986:
983:
972:
971:
959:
956:
953:
950:
947:
927:
924:
921:
898:
894:
888:
885:
882:
878:
874:
869:
865:
859:
855:
831:
826:
822:
818:
815:
812:
807:
804:
801:
797:
793:
788:
785:
782:
778:
774:
771:
768:
763:
759:
755:
735:
732:
729:
726:
723:
703:
700:
697:
694:
691:
688:
685:
665:
662:
659:
656:
653:
634:
623:
622:
611:
608:
603:
598:
594:
590:
587:
564:
542:
538:
515:
510:
506:
483:
479:
456:
452:
448:
443:
440:
437:
433:
398:
394:
367:
362:
358:
334:Main article:
331:
328:
315:
310:
306:
302:
299:
296:
291:
287:
283:
261:
258:
255:
250:
226:
209:
208:
197:
194:
191:
188:
185:
182:
179:
176:
173:
167:
161:
158:
155:
150:
147:
144:
141:
136:
132:
106:
102:
79:
53:
50:
48:
45:
33:model category
25:Kan fibrations
15:
9:
6:
4:
3:
2:
7064:
7053:
7050:
7048:
7045:
7044:
7042:
7031:
7027:
7023:
7021:0-226-51180-4
7017:
7013:
7009:
7005:
7004:May, J. Peter
7001:
6997:
6993:
6989:
6983:
6979:
6975:
6971:
6967:
6962:
6961:
6953:
6950:
6949:
6941:
6936:
6929:
6920:
6912:
6908:
6904:
6898:
6894:
6893:
6885:
6883:
6881:
6871:
6862:
6853:
6849:
6840:
6837:
6835:
6832:
6829:
6826:
6824:
6821:
6819:
6816:
6814:
6811:
6810:
6804:
6802:
6798:
6794:
6772:
6749:
6741:
6733:
6730:
6723:is a lift of
6704:
6691:
6669:
6663:
6654:
6643:
6639:
6635:
6629:
6626:
6623:
6615:
6611:
6601:
6587:
6567:
6541:
6518:
6504:
6490:
6482:
6474:
6471:
6448:
6422:
6414:
6410:
6389:
6386:
6383:
6360:
6357:
6354:
6346:
6342:
6321:
6313:
6305:
6302:
6297:
6293:
6272:
6264:
6261:
6258:
6250:
6247:
6224:
6221:
6218:
6195:
6187:
6179:
6176:
6173:
6170:
6160:
6144:
6141:
6136:
6133:
6118:
6105:
6100:
6090:
6087:
6081:
6076:
6072:
6062:
6046:
6042:
6034:
6028:
6024:
6001:
5997:
5974:
5956:
5942:
5932:
5915:
5900:
5884:
5877:
5865:
5853:
5850:
5842:
5834:
5831:
5827:
5823:
5817:
5814:
5811:
5803:
5799:
5789:
5775:
5767:
5759:
5756:
5733:
5730:
5727:
5719:
5715:
5694:
5686:
5678:
5675:
5668:and a vertex
5655:
5647:
5632:
5615:
5612:
5609:
5590:
5587:
5584:
5571:
5566:
5562:
5538:
5535:
5532:
5513:
5510:
5507:
5494:
5489:
5485:
5462:
5458:
5435:
5431:
5420:
5400:
5397:
5394:
5375:
5371:
5366:
5357:
5354:
5351:
5332:
5328:
5313:
5309:
5298:
5295:
5292:
5273:
5269:
5264:
5255:
5252:
5249:
5226:
5198:
5182:
5179:
5176:
5158:
5155:
5152:
5138:
5131:
5128:
5125:
5105:
5101:
5097:
5092:
5088:
5080:
5073:
5070:
5067:
5048:
5034:
5028:
5025:
5022:
5002:
4996:
4993:
4990:
4976:
4960:
4929:
4923:
4917:
4896:
4891:
4887:
4861:
4857:
4853:
4850:
4844:
4841:
4835:
4832:
4829:
4823:
4820:
4810:
4797:
4792:
4789:
4785:
4778:
4775:
4772:
4759:
4756:
4751:
4748:
4745:
4741:
4737:
4734:
4731:
4722:
4705:
4702:
4699:
4683:
4680:
4677:
4667:
4651:
4648:
4645:
4642:
4639:
4626:
4607:
4604:
4601:
4588:
4585:
4572:
4562:
4557:
4541:
4532:
4519:
4514:
4510:
4504:
4496:
4493:
4488:
4485:
4482:
4478:
4472:
4464:
4461:
4452:
4438:
4430:
4422:
4419:
4416:
4413:
4403:
4388:
4380:
4377:
4374:
4356:
4348:
4345:
4342:
4329:
4324:
4320:
4310:
4293:
4281:
4275:
4272:
4262:
4246:
4243:
4238:
4230:
4227:
4214:
4204:
4198:
4195:
4192:
4184:
4166:
4149:
4146:
4143:
4126:
4110:
4107:
4104:
4085:
4081:
4064:
4058:
4051:
4045:
4038:
4032:
4019:
4003:
3990:
3975:
3955:
3952:
3949:
3937:
3934:
3931:
3920:
3917:
3914:
3902:
3899:
3896:
3880:
3864:
3851:
3846:
3819:
3792:
3767:
3753:
3707:
3677:
3672:
3669:
3623:
3621:
3602:
3599:
3596:
3592:
3580:
3577:
3567:
3563:
3539:
3536:
3525:
3522:
3484:
3481:
3470:
3467:
3462:
3458:
3449:
3443:
3425:
3421:
3417:
3412:
3408:
3401:
3396:
3393:
3390:
3386:
3376:
3374:
3370:
3359:
3340:
3334:
3331:
3328:
3315:
3305:
3299:
3296:
3288:
3259:
3255:
3229:
3226:
3218:
3204:
3203:
3199:
3198:right adjoint
3189:
3172:
3166:
3144:
3141:
3138:
3111:
3108:
3105:
3092:
3074:
3071:
3068:
3043:
3040:
3037:
3007:
3004:
3001:
2997:
2993:
2990:
2987:
2982:
2979:
2976:
2972:
2968:
2963:
2960:
2957:
2953:
2949:
2944:
2940:
2936:
2931:
2928:
2925:
2921:
2917:
2914:
2911:
2906:
2902:
2895:
2892:
2884:
2881:
2878:
2874:
2870:
2867:
2864:
2859:
2855:
2845:
2840:
2836:
2825:
2824:
2823:
2806:
2798:
2795:
2792:
2788:
2778:
2770:
2766:
2762:
2757:
2753:
2723:
2720:
2717:
2713:
2709:
2706:
2703:
2698:
2694:
2690:
2687:
2684:
2679:
2676:
2673:
2669:
2665:
2662:
2659:
2654:
2650:
2643:
2640:
2632:
2629:
2626:
2622:
2618:
2615:
2612:
2607:
2603:
2593:
2588:
2584:
2573:
2572:
2571:
2554:
2546:
2543:
2540:
2536:
2526:
2518:
2514:
2510:
2505:
2501:
2473:
2465:
2461:
2455:
2451:
2447:
2441:
2435:
2428:
2427:
2426:
2412:
2389:
2381:
2373:
2370:
2363:
2362:
2361:
2347:
2327:
2307:
2287:
2277:
2258:
2247:
2244:
2235:
2234:
2231:, called the
2230:
2226:
2211:
2197:
2175:
2162:
2157:
2149:
2146:
2136:
2123:
2120:
2111:
2105:
2102:
2093:
2079:
2071:
2063:
2054:
2029:
2004:
1996:
1991:
1983:
1980:
1972:
1953:
1942:
1923:
1914:
1906:
1890:
1876:
1862:
1842:
1822:
1802:
1782:
1762:
1754:
1746:
1743:
1723:
1720:
1700:
1680:
1660:
1657:
1637:
1634:
1614:
1606:
1601:
1593:
1590:
1587:
1579:
1563:
1555:
1530:
1510:
1496:
1494:
1490:
1486:
1482:
1466:
1463:
1460:
1457:
1454:
1434:
1431:
1428:
1425:
1422:
1402:
1394:
1386:
1383:
1361:
1334:
1329:
1304:
1284:
1281:
1278:
1275:
1272:
1269:
1266:
1245:
1237:
1229:
1226:
1206:
1198:
1193:
1185:
1182:
1162:
1159:
1156:
1153:
1150:
1130:
1127:
1124:
1116:
1115:Kan fibration
1100:
1094:
1091:
1088:
1075:
1066:
1050:
1023:
1018:
990:
987:
984:
957:
954:
951:
948:
945:
925:
922:
919:
896:
892:
886:
883:
880:
876:
872:
867:
863:
857:
853:
845:
844:
843:
824:
820:
816:
813:
810:
805:
802:
799:
795:
791:
786:
783:
780:
776:
772:
769:
766:
761:
757:
730:
727:
724:
701:
698:
695:
692:
689:
686:
683:
660:
657:
654:
632:
609:
601:
596:
588:
585:
578:
577:
576:
562:
540:
513:
508:
481:
454:
441:
438:
435:
422:
418:
414:
396:
383:
365:
360:
347:
344: ≤
343:
337:
327:
308:
304:
300:
297:
294:
289:
285:
259:
256:
253:
238:
224:
214:
211:Applying the
189:
183:
177:
148:
142:
134:
122:
121:
120:
104:
91:
77:
67:
58:
44:
42:
38:
34:
30:
26:
22:
21:Kan complexes
7007:
6969:
6958:Bibliography
6928:
6919:
6891:
6870:
6861:
6852:
6693:
6603:
6510:
6162:
6064:
5958:
5791:
5643:
5635:Applications
5422:
5228:
5200:
5050:
4982:
4812:
4724:
4669:
4543:
4539:
4454:
4405:
4312:
4264:
4168:
4124:
4096:
4083:
4021:
3977:
3882:
3759:
3629:
3445:
3378:
3366:
3261:
3257:
3206:
3195:
3089:is a strong
3029:
2744:
2492:
2404:
2279:
2237:
2232:
2222:
2138:
2095:
1904:
1903:is called a
1882:
1693:-simplex in
1578:Yoneda lemma
1502:
1481:very similar
1480:
1117:if, for any
1114:
1080:
973:
624:
420:
416:
412:
381:
345:
341:
339:
210:
65:
63:
24:
20:
18:
6795:(such as a
5707:, as a set
1905:Kan complex
1483:to that of
47:Definitions
7041:Categories
6845:References
6834:∞-groupoid
6285:such that
6240:-simplice
1491:(see also
1485:fibrations
1415:such that
1259:such that
41:Daniel Kan
7006:(1992) .
6940:0809.4221
6911:837507571
6776:^
6747:→
6738:Δ
6708:^
6673:^
6658:^
6640:π
6612:π
6545:^
6488:→
6479:Δ
6411:π
6387:≥
6343:π
6319:→
6310:Δ
6303:ω
6270:→
6255:Δ
6248:ω
6193:→
6184:Δ
6177:β
6171:α
6142:≤
6091:∈
6039:∂
5971:Δ
5967:∂
5929:Δ
5923:→
5912:Δ
5908:∂
5898:↑
5892:↑
5878:α
5875:→
5862:Δ
5848:→
5839:Δ
5832:α
5800:π
5773:→
5764:Δ
5757:α
5716:π
5692:→
5683:Δ
5597:→
5567:∗
5520:→
5490:∗
5463:∗
5436:∗
5376:∗
5333:∗
5325:↓
5319:↓
5314:∗
5274:∗
5139:×
5106:∗
5093:∗
5032:↪
5000:→
4957:Δ
4907:Δ
4897:∈
4888:ι
4858:ι
4760:×
4749:×
4735:×
4687:→
4643:×
4617:→
4558:∗
4501:Δ
4497:×
4489:θ
4486:×
4469:Δ
4465:×
4436:→
4427:Δ
4423:×
4362:→
4325:∗
4321:θ
4288:→
4273:θ
4235:Δ
4231:×
4062:↦
4049:↦
4036:↦
4000:Δ
3996:→
3987:Δ
3944:↦
3909:↦
3861:Δ
3857:→
3843:Λ
3816:Δ
3789:Δ
3780:-simplex
3666:Δ
3578:≃
3573:∞
3523:≃
3518:∞
3468:≃
3394:∈
3387:∏
3306:≅
3238:→
3219:⋅
3135:Δ
3102:Δ
3065:Δ
3056:faces of
2991:…
2929:−
2915:…
2868:…
2785:→
2721:−
2707:…
2677:−
2663:…
2630:−
2616:…
2544:−
2533:→
2452:∐
2387:→
2378:Δ
2256:→
2172:Δ
2168:↪
2154:Λ
2147:ι
2124:ι
2121:∘
2115:~
2112:α
2103:α
2092:such that
2077:→
2068:Δ
2058:~
2055:α
2026:Δ
2002:→
1988:Λ
1981:α
1954:∗
1924:∗
1918:→
1760:→
1751:Δ
1612:→
1598:Λ
1561:→
1552:Δ
1464:∘
1432:∘
1400:→
1391:Δ
1358:Δ
1326:Λ
1282:∘
1270:∘
1243:→
1234:Δ
1204:→
1190:Λ
1160:≤
1154:≤
1128:≥
1098:→
1047:Δ
1015:Λ
988:−
955:≠
884:−
814:…
784:−
770:…
728:−
699:−
693:≤
687:≤
658:−
607:→
593:Λ
537:Δ
505:Λ
478:Δ
451:Δ
447:→
439:−
432:Δ
393:Δ
357:Λ
340:For each
298:…
166:Δ
131:Δ
101:Δ
70:standard
64:For each
6968:(1999).
6807:See also
5367:→
5265:→
5081:→
4786:→
4742:→
4511:→
4479:→
2214:Examples
1489:topology
912:for all
237:-simplex
90:-simplex
7030:1206474
6996:1711612
5201:(where
3879:sending
3200:to the
2190:, then
1297:(where
7028:
7018:
6994:
6984:
6909:
6899:
6694:where
6402:. For
5423:where
4813:where
380:, the
6935:arXiv
6799:or a
1447:and
1113:is a
938:with
423:maps
7016:ISBN
6982:ISBN
6907:OCLC
6897:ISBN
5644:The
5554:and
4975:. ^
4879:for
4631:Sets
4577:Sets
4219:Sets
3320:Sets
3234:Sets
2263:Sets
1219:and
1143:and
923:<
23:and
6974:doi
6803:).
6762:to
5602:Hom
5577:Hom
5525:Hom
5500:Hom
5387:Hom
5344:Hom
5285:Hom
5242:Hom
5211:Hom
5169:Hom
5145:Hom
5118:Hom
5060:Hom
4902:Hom
4765:Hom
4692:Hom
4622:Hom
4594:Hom
4568:Hom
4367:Hom
4335:Hom
4210:Hom
4179:Hom
4136:Hom
3311:Hom
3276:Top
3271:Hom
3242:Top
3093:of
2822:by
2570:by
2252:Top
1487:in
1349:in
7043::
7026:MR
7024:.
7014:.
6992:MR
6990:.
6980:.
6905:.
6879:^
6636::=
6503:.
4553:ev
3500:,
2360:,
1065:.
92:,
43:.
7032:.
6998:.
6976::
6943:.
6937::
6913:.
6773:X
6750:X
6742:0
6734::
6731:x
6705:x
6679:)
6670:x
6664:,
6655:X
6649:(
6644:n
6633:)
6630:x
6627:,
6624:X
6621:(
6616:n
6588:X
6568:X
6542:X
6519:X
6491:X
6483:0
6475::
6472:x
6452:]
6449:x
6446:[
6426:)
6423:X
6420:(
6415:0
6390:2
6384:n
6364:)
6361:x
6358:,
6355:X
6352:(
6347:n
6322:X
6314:n
6306::
6298:n
6294:d
6273:X
6265:1
6262:+
6259:n
6251::
6228:)
6225:1
6222:+
6219:n
6216:(
6196:X
6188:n
6180::
6174:,
6148:}
6145:1
6137:u
6134:e
6129:|
6123:|
6119:x
6115:|
6110:|
6106::
6101:n
6096:R
6088:x
6085:{
6082:=
6077:n
6073:B
6047:n
6043:B
6035:/
6029:n
6025:B
6002:n
5998:S
5975:n
5943:}
5933:0
5916:n
5901:x
5885:X
5866:n
5854::
5851:X
5843:n
5835::
5828:{
5824:=
5821:)
5818:x
5815:,
5812:X
5809:(
5804:n
5776:X
5768:n
5760::
5737:)
5734:x
5731:,
5728:X
5725:(
5720:n
5695:X
5687:0
5679::
5676:x
5656:X
5619:)
5616:Y
5613:,
5610:K
5607:(
5594:)
5591:Y
5588:,
5585:L
5582:(
5572::
5563:i
5542:)
5539:Y
5536:,
5533:L
5530:(
5517:)
5514:X
5511:,
5508:L
5505:(
5495::
5486:p
5459:p
5432:i
5404:)
5401:Y
5398:,
5395:K
5392:(
5372:p
5361:)
5358:X
5355:,
5352:K
5349:(
5329:i
5310:i
5302:)
5299:Y
5296:,
5293:L
5290:(
5270:p
5259:)
5256:X
5253:,
5250:L
5247:(
5186:)
5183:Y
5180:,
5177:L
5174:(
5162:)
5159:Y
5156:,
5153:K
5150:(
5135:)
5132:X
5129:,
5126:K
5123:(
5111:)
5102:p
5098:,
5089:i
5085:(
5077:)
5074:X
5071:,
5068:L
5065:(
5035:L
5029:K
5026::
5023:i
5003:Y
4997:X
4994::
4991:p
4961:n
4936:)
4933:]
4930:n
4927:[
4924:,
4921:]
4918:n
4915:[
4912:(
4892:n
4867:)
4862:n
4854:,
4851:x
4848:(
4845:f
4842:=
4839:)
4836:f
4833:,
4830:x
4827:(
4824:v
4821:e
4798:Y
4793:v
4790:e
4782:)
4779:Y
4776:,
4773:X
4770:(
4757:X
4752:g
4746:1
4738:K
4732:X
4709:)
4706:Y
4703:,
4700:X
4697:(
4684:K
4681::
4678:f
4655:)
4652:Y
4649:,
4646:K
4640:X
4637:(
4627:s
4614:)
4611:)
4608:Y
4605:,
4602:X
4599:(
4589:,
4586:K
4583:(
4573:s
4563::
4520:Y
4515:f
4505:n
4494:X
4483:1
4473:m
4462:X
4439:Y
4431:n
4420:X
4417::
4414:f
4389:m
4385:)
4381:Y
4378:,
4375:X
4372:(
4357:n
4353:)
4349:Y
4346:,
4343:X
4340:(
4330::
4297:]
4294:n
4291:[
4285:]
4282:m
4279:[
4276::
4250:)
4247:Y
4244:,
4239:n
4228:X
4225:(
4215:s
4205:=
4202:)
4199:Y
4196:,
4193:X
4190:(
4185:n
4153:)
4150:Y
4147:,
4144:X
4141:(
4111:Y
4108:,
4105:X
4065:0
4059:2
4052:1
4046:1
4039:0
4033:0
4004:1
3991:2
3959:]
3956:1
3953:,
3950:0
3947:[
3941:]
3938:1
3935:,
3932:0
3929:[
3924:]
3921:0
3918:,
3915:0
3912:[
3906:]
3903:2
3900:,
3897:0
3894:[
3865:1
3852:2
3847:0
3820:1
3793:n
3768:n
3737:G
3713:G
3708:B
3688:]
3683:G
3678:,
3673:p
3670:o
3662:[
3640:G
3606:)
3603:2
3600:,
3597:q
3593:/
3588:Z
3584:(
3581:K
3568:q
3564:L
3543:)
3540:2
3537:,
3533:Z
3529:(
3526:K
3513:P
3510:C
3488:)
3485:1
3482:,
3478:Z
3474:(
3471:K
3463:1
3459:S
3431:)
3426:i
3422:n
3418:,
3413:i
3409:A
3405:(
3402:K
3397:I
3391:i
3347:)
3344:)
3341:Y
3338:(
3335:S
3332:,
3329:X
3326:(
3316:s
3303:)
3300:Y
3297:,
3293:|
3289:X
3285:|
3281:(
3230:s
3227::
3223:|
3215:|
3176:)
3173:X
3170:(
3167:S
3145:1
3142:+
3139:n
3112:1
3109:+
3106:n
3075:1
3072:+
3069:n
3044:1
3041:+
3038:n
3026:.
3013:)
3008:1
3005:+
3002:n
2998:t
2994:,
2988:,
2983:2
2980:+
2977:i
2973:t
2969:,
2964:1
2961:+
2958:i
2954:t
2950:+
2945:i
2941:t
2937:,
2932:1
2926:i
2922:t
2918:,
2912:,
2907:0
2903:t
2899:(
2896:f
2893:=
2890:)
2885:1
2882:+
2879:n
2875:t
2871:,
2865:,
2860:0
2856:t
2852:(
2849:)
2846:f
2841:i
2837:s
2833:(
2810:)
2807:X
2804:(
2799:1
2796:+
2793:n
2789:S
2782:)
2779:X
2776:(
2771:n
2767:S
2763::
2758:i
2754:s
2729:)
2724:1
2718:n
2714:t
2710:,
2704:,
2699:i
2695:t
2691:,
2688:0
2685:,
2680:1
2674:i
2670:t
2666:,
2660:,
2655:0
2651:t
2647:(
2644:f
2641:=
2638:)
2633:1
2627:n
2623:t
2619:,
2613:,
2608:0
2604:t
2600:(
2597:)
2594:f
2589:i
2585:d
2581:(
2558:)
2555:X
2552:(
2547:1
2541:n
2537:S
2530:)
2527:X
2524:(
2519:n
2515:S
2511::
2506:i
2502:d
2489:.
2477:)
2474:X
2471:(
2466:n
2462:S
2456:n
2448:=
2445:)
2442:X
2439:(
2436:S
2413:n
2390:X
2382:n
2374::
2371:f
2348:X
2328:n
2308:n
2288:X
2276:.
2259:s
2248::
2245:S
2198:X
2176:n
2163:n
2158:k
2150::
2106:=
2080:X
2072:n
2064::
2030:n
2005:X
1997:n
1992:k
1984::
1957:}
1951:{
1927:}
1921:{
1915:X
1891:X
1863:1
1843:2
1823:2
1803:s
1783:X
1763:X
1755:n
1747::
1744:x
1724:s
1721:f
1701:Y
1681:n
1661:i
1658:y
1638:s
1635:f
1615:Y
1607:n
1602:k
1594::
1591:s
1588:f
1564:X
1556:n
1531:X
1511:n
1467:x
1461:f
1458:=
1455:y
1435:i
1429:x
1426:=
1423:s
1403:X
1395:n
1387::
1384:x
1362:n
1335:n
1330:k
1305:i
1285:i
1279:y
1276:=
1273:s
1267:f
1246:Y
1238:n
1230::
1227:y
1207:X
1199:n
1194:k
1186::
1183:s
1163:n
1157:k
1151:0
1131:1
1125:n
1101:Y
1095:X
1092::
1089:f
1051:n
1024:n
1019:k
994:)
991:1
985:n
982:(
970:.
958:k
952:j
949:,
946:i
926:j
920:i
897:i
893:s
887:1
881:j
877:d
873:=
868:j
864:s
858:i
854:d
830:)
825:n
821:s
817:,
811:,
806:1
803:+
800:k
796:s
792:,
787:1
781:k
777:s
773:,
767:,
762:0
758:s
754:(
734:)
731:1
725:n
722:(
702:1
696:n
690:k
684:0
664:)
661:1
655:n
652:(
633:n
610:X
602:n
597:k
589::
586:s
563:X
541:2
514:2
509:k
482:n
455:n
442:1
436:n
421:n
417:k
413:n
397:n
382:k
366:n
361:k
346:n
342:k
314:)
309:n
305:t
301:,
295:,
290:0
286:t
282:(
260:1
257:+
254:n
249:R
225:n
196:)
193:]
190:n
187:[
184:,
181:]
178:i
175:[
172:(
160:m
157:o
154:H
149:=
146:)
143:i
140:(
135:n
105:n
78:n
66:n
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.