17:
68:. In three dimensions, Kelly found an eight-point isosceles set, six points of which are the same; the remaining two points lie on a line perpendicular to the pentagon through its center, at the same distance as the pentagon vertices from the center. This three-dimensional example was later proven to be optimal, and to be the unique optimal solution.
265:
Despite this decomposition theorem, it is possible for the largest two-distance set and the largest isosceles set in the same dimension to have different sizes. This happens, for instance, in the plane, where the largest two-distance set has five points (the vertices of a regular pentagon), while the
261:
by adding the point at the intersection of its two subspaces must also be an isosceles set within its subspace. In this way, an isosceles set in high dimensions can sometimes be decomposed into isosceles sets in lower dimensions. On the other hand, when an isosceles set has no decomposition of this
1069:, the whole space (and any of its subsets) is an isosceles set. Therefore, ultrametric spaces are sometimes called isosceles spaces. However, not every isosceles set is ultrametric; for instance, obtuse Euclidean isosceles triangles are not ultrametric.
621:
568:
379:
930:
718:
495:
954:
798:
824:
239:
674:
1043:
647:
431:
405:
1015:
994:
974:
884:
864:
844:
758:
738:
451:
332:
304:
284:
259:
214:
194:
174:
154:
134:
114:
94:
20:
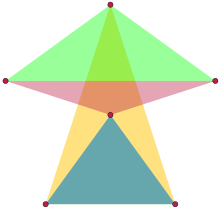
The unique 6-point isosceles set in the plane. The shaded regions show four of the 20 isosceles triangles formed by triples of these points.
508:
1323:
573:
262:
type, then it must have a stronger property than being isosceles: it has only two distances, among all pairs of points.
1246:
526:
337:
64:
showed more strongly that the unique six-point planar isosceles set consists of the vertices and center of a
932:. It has only two distances: two points formed from sums of overlapping pairs of unit vectors have distance
1200:
Kido, Hiroaki (2006), "Classification of isosceles eight-point sets in three-dimensional
Euclidean space",
266:
largest isosceles set has six points. In this case, the six-point isosceles set has a decomposition where
1045:, this construction produces a suboptimal isosceles set with seven points, the vertices and center of a
1401:
896:
679:
456:
1318:
37:
1065:, somewhat smaller upper bounds are known than for Euclidean spaces of the same dimension. In an
935:
763:
803:
36:. More precisely, each three points should determine at most two distances; this also allows
1382:
1346:
1301:
1223:
1187:
652:
1262:
8:
1022:
626:
410:
384:
219:
1149:
1129:
1107:
1046:
1000:
979:
959:
869:
849:
829:
743:
723:
436:
317:
289:
269:
244:
199:
179:
159:
139:
119:
99:
79:
61:
33:
1066:
25:
76:
Kelly's eight-point three-dimensional isosceles set can be decomposed into two sets
1368:
1332:
1287:
1258:
1250:
1209:
1175:
1141:
1099:
65:
56:. In his statement of the problem, Erdős observed that the largest such set in the
1378:
1342:
1297:
1219:
1183:
57:
49:
1179:
156:. When such a decomposition is possible, in Euclidean spaces of any dimension,
1214:
286:
is the singleton set of the central point (in a space of zero dimensions) and
1395:
1062:
1373:
1087:
956:, while two points formed from disjoint pairs of unit vectors have distance
433:
but not necessarily for other dimensions. The maximum number of points in a
53:
1292:
1058:
891:
116:(the five vertices of the pentagon), with the property that each point in
887:
1359:
Fiedler, Miroslav (1998), "Ultrametric sets in
Euclidean point spaces",
1153:
1111:
1166:
Croft, H. T. (1962), "9-point and 7-point configurations in 3-space",
523:
Lisoněk provides the following construction of two-distance sets with
32:
is a set of points with the property that every three of them form an
40:
isosceles triangles formed by three equally-spaced points on a line.
1254:
1145:
1103:
1086:
Grossman, Howard; Thebault, Victor; Schell, E. D.; Scheffe, Henry;
16:
1125:
1337:
96:(the three points on a line perpendicular to the pentagon) and
720:) denote the vector a unit distance from the origin along the
1085:
503:
216:
must be an isosceles set within its subspace, and the set
1241:
Blokhuis, A. (1983), "Chapter 7: Isosceles point sets",
1278:
Lisoněk, Petr (1997), "New maximal two-distance sets",
515:
but these numbers are not known for higher dimensions.
334:-dimensional space, an isosceles set can have at most
48:
The problem of finding the largest isosceles set in a
1025:
1003:
982:
962:
938:
899:
872:
852:
832:
806:
766:
746:
726:
682:
655:
629:
576:
529:
459:
439:
413:
387:
340:
320:
292:
272:
247:
222:
202:
182:
162:
142:
122:
102:
82:
71:
866:-dimensional subspace of points with coordinate sum
1090:(August 1946), "Problems for Solution: E731–E735",
1057:The same problem can also be considered for other
1037:
1009:
988:
968:
948:
924:
878:
858:
838:
818:
792:
752:
732:
712:
668:
641:
615:
562:
489:
445:
425:
399:
373:
326:
298:
278:
253:
233:
208:
188:
168:
148:
128:
108:
88:
601:
580:
554:
533:
365:
344:
1393:
570:points, which also produces isosceles sets with
1168:Proceedings of the London Mathematical Society
1049:, rather than the optimal eight-point set.
1236:
1234:
1232:
1124:
740:th coordinate axis, and construct the set
52:of a given dimension was posed in 1946 by
1372:
1336:
1291:
1273:
1271:
1213:
1240:
15:
1358:
1312:
1310:
1277:
1229:
1394:
1352:
1268:
501:3, 6, 8, 11, 17, 28, 30, 45 (sequence
60:has six points. In his 1947 solution,
1316:
1165:
196:must lie in perpendicular subspaces,
1361:Electronic Journal of Linear Algebra
1307:
1199:
1159:
1118:
1324:Electronic Journal of Combinatorics
1202:Electronic Journal of Combinatorics
1193:
1079:
616:{\displaystyle {\binom {d+1}{2}}+1}
13:
1247:Eindhoven University of Technology
901:
649:-dimensional Euclidean space, let
584:
537:
348:
306:consists of all remaining points.
136:is equidistant from all points of
72:Decomposition into 2-distance sets
14:
1413:
1134:The American Mathematical Monthly
1115:. See in particular problem E735.
1092:The American Mathematical Monthly
1052:
1019:isosceles set. For instance, for
563:{\displaystyle {\binom {d+1}{2}}}
374:{\displaystyle {\binom {d+2}{2}}}
453:-dimensional isosceles set, for
1280:Journal of Combinatorial Theory
925:{\displaystyle \Delta _{d+1,2}}
518:
309:
713:{\displaystyle i=1,\dots ,d+1}
490:{\displaystyle d=1,2,\dots ,8}
1:
1331:(1): Research Paper 141, 24,
1072:
7:
976:. Adding one more point to
949:{\displaystyle {\sqrt {2}}}
793:{\displaystyle e_{i}+e_{j}}
10:
1418:
381:points. This is tight for
43:
1215:10.1016/j.ejc.2005.01.003
760:consisting of all points
1180:10.1112/plms/s3-12.1.400
996:at its centroid forms a
1374:10.13001/1081-3810.1012
1317:Ionin, Yury J. (2009),
819:{\displaystyle i\neq j}
1293:10.1006/jcta.1997.2749
1132:(April 1947), "E735",
1039:
1011:
990:
970:
950:
926:
880:
860:
840:
820:
794:
754:
734:
714:
670:
643:
617:
564:
491:
447:
427:
401:
375:
328:
300:
280:
255:
235:
210:
190:
170:
150:
130:
110:
90:
21:
1040:
1012:
991:
971:
951:
927:
881:
861:
841:
821:
795:
755:
735:
715:
671:
669:{\displaystyle e_{i}}
644:
618:
565:
492:
448:
428:
402:
376:
329:
301:
281:
256:
236:
211:
191:
171:
151:
131:
111:
91:
19:
1061:. For instance, for
1023:
1001:
980:
960:
936:
897:
870:
850:
830:
804:
764:
744:
724:
680:
653:
627:
574:
527:
457:
437:
411:
385:
338:
318:
290:
270:
245:
220:
200:
180:
160:
140:
120:
100:
80:
1038:{\displaystyle d=3}
642:{\displaystyle d+1}
426:{\displaystyle d=8}
400:{\displaystyle d=6}
1249:, pp. 46–49,
1047:regular octahedron
1035:
1007:
986:
966:
946:
922:
876:
856:
836:
816:
790:
750:
730:
710:
666:
639:
613:
560:
487:
443:
423:
397:
371:
324:
296:
276:
251:
234:{\displaystyle Y'}
231:
206:
186:
166:
146:
126:
106:
86:
62:Leroy Milton Kelly
34:isosceles triangle
22:
1402:Discrete geometry
1243:Few-Distance Sets
1067:ultrametric space
1010:{\displaystyle d}
989:{\displaystyle S}
969:{\displaystyle 2}
944:
879:{\displaystyle 2}
859:{\displaystyle d}
839:{\displaystyle S}
753:{\displaystyle S}
733:{\displaystyle i}
599:
552:
497:, is known to be
446:{\displaystyle d}
363:
327:{\displaystyle d}
299:{\displaystyle Y}
279:{\displaystyle X}
254:{\displaystyle Y}
209:{\displaystyle X}
189:{\displaystyle Y}
169:{\displaystyle X}
149:{\displaystyle Y}
129:{\displaystyle X}
109:{\displaystyle Y}
89:{\displaystyle X}
26:discrete geometry
1409:
1386:
1385:
1376:
1356:
1350:
1349:
1340:
1319:"Isosceles sets"
1314:
1305:
1304:
1295:
1275:
1266:
1265:
1245:(Ph.D. thesis),
1238:
1227:
1226:
1217:
1197:
1191:
1190:
1170:, Third Series,
1163:
1157:
1156:
1122:
1116:
1114:
1083:
1044:
1042:
1041:
1036:
1018:
1016:
1014:
1013:
1008:
995:
993:
992:
987:
975:
973:
972:
967:
955:
953:
952:
947:
945:
940:
931:
929:
928:
923:
921:
920:
885:
883:
882:
877:
865:
863:
862:
857:
845:
843:
842:
837:
825:
823:
822:
817:
799:
797:
796:
791:
789:
788:
776:
775:
759:
757:
756:
751:
739:
737:
736:
731:
719:
717:
716:
711:
675:
673:
672:
667:
665:
664:
648:
646:
645:
640:
622:
620:
619:
614:
606:
605:
604:
595:
583:
569:
567:
566:
561:
559:
558:
557:
548:
536:
506:
496:
494:
493:
488:
452:
450:
449:
444:
432:
430:
429:
424:
406:
404:
403:
398:
380:
378:
377:
372:
370:
369:
368:
359:
347:
333:
331:
330:
325:
305:
303:
302:
297:
285:
283:
282:
277:
260:
258:
257:
252:
240:
238:
237:
232:
230:
215:
213:
212:
207:
195:
193:
192:
187:
175:
173:
172:
167:
155:
153:
152:
147:
135:
133:
132:
127:
115:
113:
112:
107:
95:
93:
92:
87:
66:regular pentagon
1417:
1416:
1412:
1411:
1410:
1408:
1407:
1406:
1392:
1391:
1390:
1389:
1357:
1353:
1315:
1308:
1276:
1269:
1255:10.6100/IR53747
1239:
1230:
1198:
1194:
1164:
1160:
1146:10.2307/2304710
1123:
1119:
1104:10.2307/2305860
1084:
1080:
1075:
1055:
1024:
1021:
1020:
1002:
999:
998:
997:
981:
978:
977:
961:
958:
957:
939:
937:
934:
933:
904:
900:
898:
895:
894:
871:
868:
867:
851:
848:
847:
831:
828:
827:
805:
802:
801:
784:
780:
771:
767:
765:
762:
761:
745:
742:
741:
725:
722:
721:
681:
678:
677:
660:
656:
654:
651:
650:
628:
625:
624:
600:
585:
579:
578:
577:
575:
572:
571:
553:
538:
532:
531:
530:
528:
525:
524:
521:
502:
458:
455:
454:
438:
435:
434:
412:
409:
408:
386:
383:
382:
364:
349:
343:
342:
341:
339:
336:
335:
319:
316:
315:
312:
291:
288:
287:
271:
268:
267:
246:
243:
242:
223:
221:
218:
217:
201:
198:
197:
181:
178:
177:
161:
158:
157:
141:
138:
137:
121:
118:
117:
101:
98:
97:
81:
78:
77:
74:
58:Euclidean plane
50:Euclidean space
46:
12:
11:
5:
1415:
1405:
1404:
1388:
1387:
1351:
1306:
1286:(2): 318–338,
1267:
1228:
1208:(3): 329–341,
1192:
1158:
1117:
1077:
1076:
1074:
1071:
1063:Hamming spaces
1054:
1053:Generalization
1051:
1034:
1031:
1028:
1006:
985:
965:
943:
919:
916:
913:
910:
907:
903:
875:
855:
835:
815:
812:
809:
787:
783:
779:
774:
770:
749:
729:
709:
706:
703:
700:
697:
694:
691:
688:
685:
663:
659:
638:
635:
632:
612:
609:
603:
598:
594:
591:
588:
582:
556:
551:
547:
544:
541:
535:
520:
517:
513:
512:
486:
483:
480:
477:
474:
471:
468:
465:
462:
442:
422:
419:
416:
396:
393:
390:
367:
362:
358:
355:
352:
346:
323:
311:
308:
295:
275:
250:
229:
226:
205:
185:
165:
145:
125:
105:
85:
73:
70:
45:
42:
9:
6:
4:
3:
2:
1414:
1403:
1400:
1399:
1397:
1384:
1380:
1375:
1370:
1366:
1362:
1355:
1348:
1344:
1339:
1334:
1330:
1326:
1325:
1320:
1313:
1311:
1303:
1299:
1294:
1289:
1285:
1281:
1274:
1272:
1264:
1260:
1256:
1252:
1248:
1244:
1237:
1235:
1233:
1225:
1221:
1216:
1211:
1207:
1203:
1196:
1189:
1185:
1181:
1177:
1173:
1169:
1162:
1155:
1151:
1147:
1143:
1139:
1135:
1131:
1127:
1121:
1113:
1109:
1105:
1101:
1097:
1093:
1089:
1082:
1078:
1070:
1068:
1064:
1060:
1059:metric spaces
1050:
1048:
1032:
1029:
1026:
1004:
983:
963:
941:
917:
914:
911:
908:
905:
893:
889:
873:
853:
833:
813:
810:
807:
785:
781:
777:
772:
768:
747:
727:
707:
704:
701:
698:
695:
692:
689:
686:
683:
661:
657:
636:
633:
630:
610:
607:
596:
592:
589:
586:
549:
545:
542:
539:
516:
510:
505:
500:
499:
498:
484:
481:
478:
475:
472:
469:
466:
463:
460:
440:
420:
417:
414:
394:
391:
388:
360:
356:
353:
350:
321:
307:
293:
273:
263:
248:
227:
224:
203:
183:
163:
143:
123:
103:
83:
69:
67:
63:
59:
55:
51:
41:
39:
35:
31:
30:isosceles set
27:
18:
1364:
1360:
1354:
1338:10.37236/230
1328:
1322:
1283:
1282:, Series A,
1279:
1242:
1205:
1201:
1195:
1171:
1167:
1161:
1137:
1133:
1130:Kelly, L. M.
1120:
1095:
1091:
1081:
1056:
1017:-dimensional
892:hypersimplex
846:lies in the
522:
519:Construction
514:
313:
310:Upper bounds
264:
241:formed from
75:
47:
29:
23:
1174:: 400–424,
1126:Erdős, Paul
1088:Erdős, Paul
888:convex hull
623:points. In
1263:0516.05017
1140:(4): 227,
1098:(7): 394,
1073:References
54:Paul Erdős
38:degenerate
1367:: 23–30,
902:Δ
811:≠
696:…
479:…
1396:Category
407:and for
228:′
1383:1615350
1347:2577309
1302:1429084
1224:2206471
1188:0155230
1154:2304710
1112:2305860
890:is the
826:. Then
507:in the
504:A175769
44:History
1381:
1345:
1300:
1261:
1222:
1186:
1152:
1110:
886:; its
1150:JSTOR
1108:JSTOR
676:(for
28:, an
800:for
509:OEIS
176:and
1369:doi
1333:doi
1288:doi
1259:Zbl
1251:doi
1210:doi
1176:doi
1142:doi
1100:doi
314:In
24:In
1398::
1379:MR
1377:,
1363:,
1343:MR
1341:,
1329:16
1327:,
1321:,
1309:^
1298:MR
1296:,
1284:77
1270:^
1257:,
1231:^
1220:MR
1218:,
1206:27
1204:,
1184:MR
1182:,
1172:12
1148:,
1138:54
1136:,
1128:;
1106:,
1096:53
1094:,
1371::
1365:3
1335::
1290::
1253::
1212::
1178::
1144::
1102::
1033:3
1030:=
1027:d
1005:d
984:S
964:2
942:2
918:2
915:,
912:1
909:+
906:d
874:2
854:d
834:S
814:j
808:i
786:j
782:e
778:+
773:i
769:e
748:S
728:i
708:1
705:+
702:d
699:,
693:,
690:1
687:=
684:i
662:i
658:e
637:1
634:+
631:d
611:1
608:+
602:)
597:2
593:1
590:+
587:d
581:(
555:)
550:2
546:1
543:+
540:d
534:(
511:)
485:8
482:,
476:,
473:2
470:,
467:1
464:=
461:d
441:d
421:8
418:=
415:d
395:6
392:=
389:d
366:)
361:2
357:2
354:+
351:d
345:(
322:d
294:Y
274:X
249:Y
225:Y
204:X
184:Y
164:X
144:Y
124:X
104:Y
84:X
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.