633:, who formalized a new theory of proportion that took into account commensurable as well as incommensurable quantities. Central to his idea was the distinction between magnitude and number. A magnitude "...was not a number but stood for entities such as line segments, angles, areas, volumes, and time which could vary, as we would say, continuously. Magnitudes were opposed to numbers, which jumped from one value to another, as from 4 to 5". Numbers are composed of some smallest, indivisible unit, whereas magnitudes are infinitely reducible. Because no quantitative values were assigned to magnitudes, Eudoxus was then able to account for both commensurable and incommensurable ratios by defining a ratio in terms of its magnitude, and proportion as an equality between two ratios. By taking quantitative values (numbers) out of the equation, he avoided the trap of having to express an irrational number as a number. "Eudoxus' theory enabled the Greek mathematicians to make tremendous progress in geometry by supplying the necessary logical foundation for incommensurable ratios". This incommensurability is dealt with in Euclid's Elements, Book X, Proposition 9. It was not until
618:, who questioned the conception that quantities are discrete and composed of a finite number of units of a given size. Past Greek conceptions dictated that they necessarily must be, for "whole numbers represent discrete objects, and a commensurable ratio represents a relation between two collections of discrete objects", but Zeno found that in fact " in general are not discrete collections of units; this is why ratios of incommensurable appear... .uantities are, in other words, continuous". What this means is that contrary to the popular conception of the time, there cannot be an indivisible, smallest unit of measure for any quantity. In fact, these divisions of quantity must necessarily be
5305:
611:, or inexpressible. Hippasus, however, was not lauded for his efforts: according to one legend, he made his discovery while out at sea, and was subsequently thrown overboard by his fellow Pythagoreans 'for having produced an element in the universe which denied the... doctrine that all phenomena in the universe can be reduced to whole numbers and their ratios.' Another legend states that Hippasus was merely exiled for this revelation. Whatever the consequence to Hippasus himself, his discovery posed a very serious problem to Pythagorean mathematics, since it shattered the assumption that numbers and geometry were inseparable; a foundation of their theory.
179:
31:
1131:
6036:
622:. For example, consider a line segment: this segment can be split in half, that half split in half, the half of the half in half, and so on. This process can continue infinitely, for there is always another half to be split. The more times the segment is halved, the closer the unit of measure comes to zero, but it never reaches exactly zero. This is just what Zeno sought to prove. He sought to prove this by formulating
626:, which demonstrated the contradictions inherent in the mathematical thought of the time. While Zeno's paradoxes accurately demonstrated the deficiencies of contemporary mathematical conceptions, they were not regarded as proof of the alternative. In the minds of the Greeks, disproving the validity of one view did not necessarily prove the validity of another, and therefore, further investigation had to occur.
343:. The Pythagorean method would have claimed that there must be some sufficiently small, indivisible unit that could fit evenly into one of these lengths as well as the other. Hippasus in the 5th century BC, however, was able to deduce that there was no common unit of measure, and that the assertion of such an existence was a contradiction. He did this by demonstrating that if the
849:"It will be a rational (magnitude) when we, for instance, say 10, 12, 3%, 6%, etc., because its value is pronounced and expressed quantitatively. What is not rational is irrational and it is impossible to pronounce and represent its value quantitatively. For example: the roots of numbers such as 10, 15, 20 which are not squares, the sides of numbers which are not cubes
665:
to the third power. Also crucial to Zeno's work with incommensurable magnitudes was the fundamental focus on deductive reasoning that resulted from the foundational shattering of earlier Greek mathematics. The realization that some basic conception within the existing theory was at odds with reality
640:
As a result of the distinction between number and magnitude, geometry became the only method that could take into account incommensurable ratios. Because previous numerical foundations were still incompatible with the concept of incommensurability, Greek focus shifted away from numerical conceptions
3432:
is not valid, so it is not true that every real number is rational or irrational. Thus, the notion of an irrational number bifurcates into multiple distinct notions. One could take the traditional definition of an irrational number as a real number that is not rational. However, there is a second
1910:
The decimal expansion of an irrational number never repeats (meaning the decimal expansion does not repeat the same number or sequence of numbers) or terminates (this means there is not a finite number of nonzero digits), unlike any rational number. The same is true for
2659:
3633:: that is, there is a metric on the irrationals inducing the same topology as the restriction of the Euclidean metric, but with respect to which the irrationals are complete. One can see this without knowing the aforementioned fact about G-delta sets: the
674:
that "...established the deductive organization on the basis of explicit axioms..." as well as "...reinforced the earlier decision to rely on deductive reasoning for proof". This method of exhaustion is the first step in the creation of calculus.
4496:
period, but such claims are not well substantiated. The case for early Hindu awareness of incommensurable magnitudes is rendered most unlikely by the lack of evidence that Indian mathematicians of that period had come to grips with fundamental
2028:
Here the repetend is 162 and the length of the repetend is 3. First, we multiply by an appropriate power of 10 to move the decimal point to the right so that it is just in front of a repetend. In this example we would multiply by 10 to obtain:
139:
exactly, nor does it repeat. Conversely, a decimal expansion that terminates or repeats must be a rational number. These are provable properties of rational numbers and positional number systems and are not used as definitions in mathematics.
87:, meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.
3302:
1746:
4114:
2476:
1051:, closely related to irrational numbers (and due to Cataldi, 1613), received attention at the hands of Euler, and at the opening of the 19th century were brought into prominence through the writings of
844:
and cubic irrationals. He provided definitions for rational and irrational magnitudes, which he treated as irrational numbers. He dealt with them freely but explains them in geometric terms as follows:
737:
Later, in their treatises, Indian mathematicians wrote on the arithmetic of surds including addition, subtraction, multiplication, rationalization, as well as separation and extraction of square roots.
2263:
869:"their sums or differences, or results of their addition to a rational magnitude, or results of subtracting a magnitude of this kind from an irrational one, or of a rational magnitude from it."
641:
such as algebra and focused almost exclusively on geometry. In fact, in many cases, algebraic conceptions were reformulated into geometric terms. This may account for why we still conceive of
2128:
3637:
expansion of an irrational number defines a homeomorphism from the space of irrationals to the space of all sequences of positive integers, which is easily seen to be completely metrizable.
1534:
The number 2 raised to any positive integer power must be even (because it is divisible by 2) and the number 3 raised to any positive integer power must be odd (since none of its
901:
mathematician Al-Hashimi provided general proofs (rather than geometric demonstrations) for irrational numbers, as he considered multiplication, division, and other arithmetical functions.
2023:
2071:
961:
2522:
1372:
3640:
Furthermore, the set of all irrationals is a disconnected metrizable space. In fact, the irrationals equipped with the subspace topology have a basis of clopen groups so the space is
2784:
3611:
2939:
3621:. Restricting the Euclidean distance function gives the irrationals the structure of a metric space. Since the subspace of irrationals is not closed, the induced metric is not
1483:
2514:
3901:
3863:
3825:
3787:
3749:
3487:
2720:
924:
and denominators are separated by a horizontal bar. In his discussion he writes, "..., for example, if you are told to write three-fifths and a third of a fifth, write thus,
5533:
1021:. Méray had taken in 1869 the same point of departure as Heine, but the theory is generally referred to the year 1872. Weierstrass's method has been completely set forth by
5848:
5771:
5732:
5694:
5666:
5638:
5610:
5498:
5465:
5437:
5409:
3207:
2871:
1529:
320:
298:
276:
254:
232:
210:
2211:
1809:
614:
The discovery of incommensurable ratios was indicative of another problem facing the Greeks: the relation of the discrete to the continuous. This was brought to light by
3181:
2828:
3027:
2989:
1419:
3360:
3149:
637:
developed a theory of proportion that took into account irrational as well as rational ratios that a strong mathematical foundation of irrational numbers was created.
3415:
3328:
3091:
3065:
1073: = 0). While Lambert's proof is often called incomplete, modern assessments support it as satisfactory, and in fact for its time it is unusually rigorous.
3389:
1776:
3117:
592:
must be even. Hence they have a common factor of 2. However, this contradicts the assumption that they have no common factors. This contradiction proves that
3527:
3507:
3451:
4627:
666:
necessitated a complete and thorough investigation of the axioms and assumptions that underlie that theory. Out of this necessity, Eudoxus developed his
4510:
995:, the proof of the existence of transcendental numbers, and the resurgence of the scientific study of the theory of irrationals, largely ignored since
2080:
is the length of the repetend. This has the effect of moving the decimal point to be in front of the "next" repetend. In our example, multiply by 10:
1037:, separating them into two groups having certain characteristic properties. The subject has received later contributions at the hands of Weierstrass,
828:, developed the theory of composite ratios, and extended the concept of number to ratios of continuous magnitude. In his commentary on Book 10 of the
1538:
will be 2). Clearly, an integer cannot be both odd and even at the same time: we have a contradiction. The only assumption we made was that log
355:
with a leg, then one of those lengths measured in that unit of measure must be both odd and even, which is impossible. His reasoning is as follows:
1105:(1882), starting from Hermite's conclusions, showed the same for π. Lindemann's proof was much simplified by Weierstrass (1885), still further by
857:
In contrast to Euclid's concept of magnitudes as lines, Al-Mahani considered integers and fractions as rational magnitudes, and square roots and
3215:
2133:
The result of the two multiplications gives two different expressions with exactly the same "decimal portion", that is, the tail end of 10,000
1619:
5083:
1090:
761:
4854:
Jarden, Dov (1953). "Curiosa No. 339: A simple proof that a power of an irrational number to an irrational exponent may be rational".
2421:
1877:
of the real numbers, many irrational real numbers can be constructed by combining transcendental and algebraic numbers. For example, 3
1272:
in the denominator that does not divide into the numerator whatever power each is raised to. Therefore, if an integer is not an exact
3529:
is positive. This definition is stronger than the traditional definition of an irrational number. This second definition is used in
1264:
into primes. Using it we can show that if a rational number is not an integer then no integral power of it can be an integer, as in
144:
5359:
1848:
is an irrational algebraic number. There are countably many algebraic numbers, since there are countably many integer polynomials.
1973:− 1 steps without using any remainder more than once. After that, a remainder must recur, and then the decimal expansion repeats.
4600:
685:
of whole numbers up to 17, but stopped there probably because the algebra he used could not be applied to the square root of 17.
1195:
905:
2481:
The base of the left side is irrational and the right side is rational, so one must prove that the exponent on the left side,
1167:
4977:
4178:
2222:
693:
Geometrical and mathematical problems involving irrational numbers such as square roots were addressed very early during the
5051:
1081:, provided a proof to show that π is irrational, whence it follows immediately that π is irrational also. The existence of
5548:
1029:(1894). Weierstrass, Cantor, and Heine base their theories on infinite series, while Dedekind founds his on the idea of a
1174:
1025:
in 1880, and
Dedekind's has received additional prominence through the author's later work (1888) and the endorsement by
5543:
1969:. If 0 appears as a remainder, the decimal expansion terminates. If 0 never occurs, then the algorithm can run at most
1148:
17:
2086:
5006:
4890:
4690:
4448:
2874:
1257:
1214:
917:
4770:
3629:—i.e., a countable intersection of open subsets—in a complete metric space, the space of irrationals is
878:
4998:
4682:
4440:
2654:{\displaystyle \log _{\sqrt {2}}3={\frac {\log _{2}3}{\log _{2}{\sqrt {2}}}}={\frac {\log _{2}3}{1/2}}=2\log _{2}3}
1986:
1181:
5503:
2035:
927:
5921:
5076:
5999:
1328:
1055:. Dirichlet also added to the general theory, as have numerous contributors to the applications of the subject.
127:, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor
4738:"Saggio di una introduzione alla teoria delle funzioni analitiche secondo i principii del prof. C. Weierstrass"
4477:
1152:
600:
cannot both be integers and thus the existence of a number that cannot be expressed as a ratio of two integers.
352:
83:
1163:
6065:
5882:
3308:
2725:
2409:
2370:
805:
155:
5210:
4525:
3682:
3563:
5352:
4632:
4595:
2883:
1078:
5304:
4760:"Mémoire sur quelques propriétés remarquables des quantités transcendentes, circulaires et logarithmiques"
749:(in 629 AD) made contributions in this area as did other mathematicians who followed. In the 12th century
6060:
5508:
4864:
4034:
1427:
148:
2484:
1818: = (2 + 1). It is clearly algebraic since it is the root of an integer polynomial, (
5069:
3673:
81:
of lengths of two line segments is an irrational number, the line segments are also described as being
3534:
5916:
5872:
5279:
3880:
3842:
3804:
3766:
3728:
3663:
3460:
2675:
97:
5514:
4492:
It has been claimed also that the first recognition of incommensurables appears in India during the
1240:
is another famous quadratic irrational number. The square roots of all natural numbers that are not
6039:
5911:
4605:
3425:
865:
approach to the concept of irrationality, as he attributes the following to irrational magnitudes:
348:
5831:
5754:
5715:
5677:
5649:
5621:
5593:
5481:
5448:
5420:
5392:
3190:
2833:
1491:
303:
281:
259:
237:
215:
193:
5345:
4755:
4737:
2187:
1781:
1141:
1102:
1058:
817:
775:
757:
3154:
2789:
5140:
3641:
3184:
2998:
2960:
2665:
1383:
1296:
1188:
992:
5165:
4430:
T. K. Puttaswamy, "The
Accomplishments of Ancient Indian Mathematicians", pp. 411–2, in
3336:
3122:
2516:, is irrational. This is so because, by the formula relating logarithms with different bases,
904:
Many of these concepts were eventually accepted by
European mathematicians sometime after the
5984:
5820:
5321:
5103:
5024:
4797:
4199:
4041:
3668:
3630:
3394:
3313:
3304:
2381:
1912:
1860:
1831:
1598:
1082:
1074:
1052:
3070:
3044:
5737:
5470:
5326:
5316:
4969:
4931:
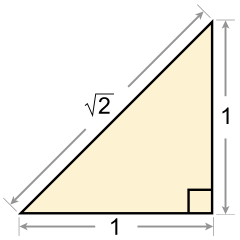
4841:
4641:
4555:
4100:
3701:
3365:
1754:
1261:
1245:
841:
671:
667:
8:
5948:
5858:
5815:
5797:
5575:
5160:
5150:
5133:
4591:
4465:
3622:
3096:
1924:
1874:
1022:
1009:
784:
779:
734:, however, writes that "such claims are not well substantiated and unlikely to be true".
731:
678:
623:
402:
124:
4946:
4832:
Fowler, David H. (2001), "The story of the discovery of incommensurability, revisited",
4645:
4168:
3433:
definition of an irrational number used in constructive mathematics, that a real number
5853:
5565:
4814:
4657:
4653:
4572:
4389:
4381:
4267:
4259:
4224:
4216:
4142:
3634:
3557:
3512:
3492:
3454:
3436:
2277:
1590:
1048:
964:
882:
719:
109:
6011:
5938:
5877:
5863:
5558:
5538:
5235:
5200:
5178:
5002:
4973:
4886:
4818:
4686:
4661:
4483:
4473:
4444:
4393:
4271:
4228:
4174:
4146:
4134:
4096:
3989:
3658:
3618:
1977:
1554: ≠ 0). The contradiction means that this assumption must be false, i.e. log
1038:
980:
634:
630:
604:
128:
753:
evaluated some of these formulas and critiqued them, identifying their limitations.
6029:
5958:
5933:
5867:
5776:
5742:
5583:
5553:
5475:
5378:
5272:
5267:
5245:
5230:
5195:
5113:
4905:
Lord, Nick, "Maths bite: irrational powers of irrational numbers can be rational",
4806:
4649:
4564:
4377:
4373:
4251:
4242:
James R. Choike (1980). "The
Pentagram and the Discovery of an Irrational Number".
4208:
4126:
4064:
4027:
3947:
3932:
3696:
3691:
2393:
1610:
1586:
1233:
1018:
1000:
991:
in the 19th century entailed the differentiation of irrationals into algebraic and
976:
35:
4291:, Vol. 1. New York: Oxford University Press (original work published 1972), p. 33.
1042:
331:
The first proof of the existence of irrational numbers is usually attributed to a
5906:
5810:
5442:
5055:
5048:
4837:
4164:
3982:
3799:
3429:
1241:
1094:
1093:, which showed that every interval in the reals contains transcendental numbers.
1034:
765:
163:
70:
4630:(1987). "The theory of quadratic irrationals in medieval Oriental mathematics".
881:(c. 850 – 930) was the first to accept irrational numbers as solutions to
178:
5953:
5943:
5928:
5747:
5615:
5386:
5128:
5118:
4550:
4194:
3975:
3875:
3723:
2873:, which is a contradictory pair of prime factorizations and hence violates the
1931:
1927:
1830: − 1 = 0. This polynomial has no rational roots, since the
988:
984:
833:
332:
113:
4877:
4130:
750:
57:
6054:
6016:
5989:
5898:
5183:
5145:
4432:
4138:
3716:
3653:
3550:
3530:
1980:, we can prove that it is a fraction of two integers. For example, consider:
1950:
1110:
1106:
718:
It is suggested that the concept of irrationality was implicitly accepted by
711:
183:
117:
1558: 3 is irrational, and can never be expressed as a quotient of integers
746:
30:
5979:
5781:
5250:
5220:
4284:
4160:
4115:"95.42 Irrational square roots of natural numbers — a geometrical approach"
3925:
3614:
1535:
1269:
1265:
1237:
1086:
1030:
1026:
1014:
1004:
920:
during the 12th century, first mentions the use of a fractional bar, where
694:
615:
103:
4487:
2880:
A stronger result is the following: Every rational number in the interval
909:
5805:
5587:
4759:
4197:(1945). "The Discovery of Incommensurability by Hippasus of Metapontum".
3761:
3626:
3546:
1920:
1114:
886:
821:
797:
742:
727:
159:
66:
48:
3297:{\displaystyle \pi e,\ \pi /e,\ \pi ^{e},\ \pi ^{\sqrt {2}},\ \ln \pi ,}
1741:{\displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=0\;,}
1256:
The proof above for the square root of two can be generalized using the
5786:
5643:
4810:
4576:
4385:
4263:
4220:
2369:
Although the above argument does not decide between the two cases, the
1856:
1594:
862:
730:
of numbers such as 2 and 61 could not be exactly determined. Historian
344:
167:
73:. That is, irrational numbers cannot be expressed as the ratio of two
5061:
4410:"Ritual Geometry in India and its Parallelism in other Culture Areas"
4409:
3331:
2957:. Similarly, every positive rational number can be written either as
1962:
1292:
921:
858:
837:
359:
Start with an isosceles right triangle with side lengths of integers
340:
4788:
4568:
4255:
4212:
1130:
5894:
5825:
5671:
5034:
Rolf
Wallisser, "On Lambert's proof of the irrationality of π", in
4679:
Mathematics Across
Cultures: The History of Non-western Mathematics
4437:
Mathematics Across
Cultures: The History of Non-western Mathematics
3966:
1277:
963:." This same fractional notation appears soon after in the work of
894:
890:
705:
682:
619:
336:
5038:, Franz Halter-Koch and Robert F. Tichy, (2000), Walter de Gruyter
4966:
Real
Analysis: A Constructive Approach through Interval Arithmetic
4170:
Contributions to the
Founding of the Theory of Transfinite Numbers
1542: 3 is rational (and so expressible as a quotient of integers
135:
starts with 3.14159, but no finite number of digits can represent
5414:
5337:
4921:
Marshall, Ash J., and Tan, Yiren, "A rational number of the form
3837:
801:
699:
74:
3093:) is irrational. In fact, there is no pair of non-zero integers
2471:{\displaystyle \left({\sqrt {2}}\right)^{\log _{\sqrt {2}}3}=3.}
2408:
is a transcendental number (there can be more than one value if
5368:
996:
813:
723:
339:), who probably discovered them while identifying sides of the
1867:
and π, which are transcendental for all nonzero rational
1291:
Perhaps the numbers most easy to prove irrational are certain
123:
Like all real numbers, irrational numbers can be expressed in
3553:
subset, the complementary set of irrationals is uncountable.
3457:
from every rational number, or equivalently, if the distance
1916:
874:
825:
812:. Middle Eastern mathematicians also merged the concepts of "
78:
4992:
4364:
Robert L. McCabe (1976). "Theodorus' Irrationality Proofs".
1597:
with integer coefficients. Those that are not algebraic are
96:
of a circle's circumference to its diameter, Euler's number
3909:
898:
697:
in India. There are references to such calculations in the
3917:
1085:
was first established by
Liouville (1844, 1851). Later,
913:
371:. The ratio of the hypotenuse to a leg is represented by
187:
4711:. La Salle, Illinois: The Open Court Publishing Company.
2415:
An example that provides a simple constructive proof is
2268:
is a ratio of integers and therefore a rational number.
5289:
2258:{\displaystyle A={\frac {7155}{9990}}={\frac {53}{74}}}
1276:
th power of another integer, then that first integer's
999:. The year 1872 saw the publication of the theories of
770:
91:
4509:
Datta, Bibhutibhusan; Singh, Awadhesh Narayan (1993).
5834:
5757:
5718:
5680:
5652:
5624:
5596:
5517:
5484:
5451:
5423:
5395:
4589:
3883:
3845:
3807:
3769:
3731:
3566:
3515:
3495:
3463:
3439:
3397:
3368:
3339:
3316:
3218:
3193:
3157:
3125:
3099:
3073:
3047:
3001:
2963:
2886:
2836:
2792:
2728:
2678:
2525:
2487:
2424:
2225:
2190:
2089:
2038:
1989:
1784:
1757:
1622:
1494:
1430:
1386:
1331:
930:
306:
284:
262:
240:
218:
196:
4952:. Department of Mathematics, University of Oklahoma.
4767:
Mémoires de l'Académie royale des sciences de Berlin
3151:
is irrational. Moreover, it is not known if the set
2664:
which we can assume, for the sake of establishing a
4735:
4676:
4675:Jacques Sesiano, "Islamic mathematics", p. 148, in
4431:
4308:
4306:
1923:expansions, and in general for expansions in every
1834:shows that the only possibilities are ±1, but
1236:was likely the first number proved irrational. The
1155:. Unsourced material may be challenged and removed.
5842:
5765:
5726:
5688:
5660:
5632:
5604:
5527:
5492:
5459:
5431:
5403:
4339:
3895:
3857:
3819:
3781:
3743:
3605:
3521:
3501:
3481:
3445:
3409:
3383:
3354:
3330:are irrational. It is not known if either of the
3322:
3296:
3201:
3175:
3143:
3111:
3085:
3059:
3021:
2983:
2933:
2865:
2822:
2778:
2714:
2653:
2508:
2470:
2257:
2205:
2122:
2065:
2017:
1811:. An example of an irrational algebraic number is
1803:
1770:
1740:
1523:
1477:
1413:
1366:
1061:proved (1761) that π cannot be rational, and that
955:
314:
292:
278:). The real numbers also include the irrationals (
270:
248:
226:
204:
4289:Mathematical Thought from Ancient to Modern Times
782:provided proofs for these infinite series in the
6052:
5036:Algebraic Number Theory and Diophantine Analysis
4954:(Senior Mathematics Seminar, Spring 2008 course)
4553:(1995). "Ideas of Calculus in Islam and India".
4363:
4303:
2384:, hence irrational. This theorem states that if
2123:{\displaystyle 10,000A=7\,162.162\,162\,\ldots }
1314: 3 is rational. For some positive integers
861:as irrational magnitudes. He also introduced an
607:termed this ratio of incommensurable magnitudes
4876:George, Alexander; Velleman, Daniel J. (2002).
4622:
4620:
4618:
4616:
4241:
1613:are the real solutions of polynomial equations
4875:
4193:
3419:
5353:
5077:
4677:Selin, Helaine; D'Ambrosio, Ubiratan (2000).
3535:proof that the square root of 2 is irrational
2018:{\displaystyle A=0.7\,162\,162\,162\,\ldots }
131:. For example, the decimal representation of
4963:
4626:
4613:
3600:
3588:
3476:
3464:
3170:
3158:
2404:is not a rational number, then any value of
2066:{\displaystyle 10A=7.162\,162\,162\,\ldots }
1822: − 1) = 2, which is equivalent to
956:{\displaystyle {\frac {3\quad 1}{5\quad 3}}}
808:allowed irrational numbers to be treated as
143:Irrational numbers can also be expressed as
4917:
4915:
4709:A History of Mathematical Notations (Vol.1)
4596:"Arabic mathematics: forgotten brilliance?"
1244:are irrational and a proof may be found in
1109:(1893), and was finally made elementary by
6035:
5360:
5346:
5084:
5070:
4633:Annals of the New York Academy of Sciences
4508:
4342:The historical development of the calculus
3887:
3849:
3811:
3773:
3735:
2076:Now we multiply this equation by 10 where
1902:are irrational (and even transcendental).
1734:
1367:{\displaystyle \log _{2}3={\frac {m}{n}}.}
762:Kerala school of astronomy and mathematics
726:(c. 750 – 690 BC) believed that the
5836:
5759:
5720:
5682:
5654:
5626:
5598:
5486:
5453:
5425:
5397:
4947:"Some unsolved problems in number theory"
4458:
4097:The 15 Most Famous Transcendental Numbers
3889:
3851:
3813:
3775:
3737:
3540:
3195:
2116:
2112:
2108:
2059:
2055:
2051:
2011:
2007:
2003:
1999:
1937:To show this, suppose we divide integers
1215:Learn how and when to remove this message
308:
286:
264:
242:
220:
198:
4912:
4666:See in particular pp. 254 & 259–260.
4244:The Two-Year College Mathematics Journal
2280:that there exist two irrational numbers
1976:Conversely, suppose we are faced with a
1260:. This asserts that every integer has a
177:
29:
5049:Zeno's Paradoxes and Incommensurability
4993:Errett Bishop; Douglas Bridges (1985).
4754:
4601:MacTutor History of Mathematics Archive
4112:
2779:{\displaystyle 2^{\log _{2}3}=2^{m/2n}}
1307: 3 ≈ 1.58 > 0).
979:become a powerful tool in the hands of
768:for several irrational numbers such as
90:Among irrational numbers are the ratio
14:
6053:
5091:
4853:
4831:
4786:
4723:
4706:
4159:
3606:{\displaystyle d(x,y)=\vert x-y\vert }
906:Latin translations of the 12th century
570:is divisible by 2, and therefore even.
452:is divisible by 2, and therefore even.
256:), which include the natural numbers (
27:Number that is not a ratio of integers
5341:
5065:
4464:
4435:; D'Ambrosio, Ubiratan, eds. (2000).
2934:{\displaystyle ((1/e)^{1/e},\infty )}
1905:
1873:Because the algebraic numbers form a
840:(d. 874/884) examined and classified
394:are in the smallest possible terms (
4549:
4518:Indian Journal of History of Science
4472:(2nd ed.). Wiley. p. 208.
4414:Indian Journal of History of Science
2271:
1153:adding citations to reliable sources
1124:
429:. (Since the triangle is isosceles,
5549:Set-theoretically definable numbers
4407:
1478:{\displaystyle (2^{m/n})^{n}=3^{n}}
1089:(1873) proved their existence by a
756:During the 14th to 16th centuries,
145:non-terminating continued fractions
24:
5520:
5367:
5018:
4944:
4654:10.1111/j.1749-6632.1987.tb37206.x
3549:set, of which the rationals are a
2925:
2509:{\displaystyle \log _{\sqrt {2}}3}
2177:cancels out the tail end of 10,000
2165:Therefore, when we subtract the 10
1577: 2 can be treated similarly.
987:. The completion of the theory of
25:
6077:
5042:
3453:is an irrational number if it is
3036:
2875:fundamental theorem of arithmetic
2303:; if this is rational, then take
1851:
1258:fundamental theorem of arithmetic
918:Islamic inheritance jurisprudence
774:and certain irrational values of
326:
6034:
5303:
4776:from the original on 2016-04-28.
4103:. URL retrieved 24 October 2007.
1251:
1129:
970:
912:, a Moroccan mathematician from
893:in the form of square roots and
791:
681:proved the irrationality of the
212:), which include the rationals (
112:. In fact, all square roots of
5058:(n.d.). Retrieved April 1, 2008
4986:
4957:
4938:
4899:
4869:
4847:
4825:
4780:
4748:
4729:
4716:
4700:
4669:
4583:
4543:
4502:
4424:
4401:
4357:
4348:
4333:
4324:
4113:Jackson, Terence (2011-07-01).
3896:{\displaystyle :\;\mathbb {N} }
3858:{\displaystyle :\;\mathbb {Z} }
3820:{\displaystyle :\;\mathbb {Q} }
3782:{\displaystyle :\;\mathbb {R} }
3744:{\displaystyle :\;\mathbb {C} }
3482:{\displaystyle \vert r-q\vert }
2715:{\displaystyle \log _{2}3=m/2n}
1227:
1140:needs additional citations for
946:
937:
722:since the 7th century BC, when
234:), which include the integers (
5528:{\displaystyle {\mathcal {P}}}
4378:10.1080/0025570X.1976.11976579
4315:
4294:
4278:
4235:
4187:
4153:
4106:
4090:
3582:
3570:
3119:for which it is known whether
2928:
2905:
2890:
2887:
2877:(unique prime factorization).
1953:is applied to the division of
1632:
1626:
1453:
1431:
1079:Bessel–Clifford function
1077:(1794), after introducing the
824:, criticized Euclid's idea of
820:" into a more general idea of
13:
1:
5883:Plane-based geometric algebra
4084:
3391:is rational for some integer
2410:complex number exponentiation
2276:Dov Jarden gave a simple non-
1286:
1003:(by his pupil Ernst Kossak),
584:We have just shown that both
398:they have no common factors).
170:real numbers are irrational.
129:end with a repeating sequence
5843:{\displaystyle \mathbb {S} }
5766:{\displaystyle \mathbb {C} }
5727:{\displaystyle \mathbb {R} }
5689:{\displaystyle \mathbb {O} }
5661:{\displaystyle \mathbb {H} }
5633:{\displaystyle \mathbb {C} }
5605:{\displaystyle \mathbb {R} }
5493:{\displaystyle \mathbb {A} }
5460:{\displaystyle \mathbb {Q} }
5432:{\displaystyle \mathbb {Z} }
5404:{\displaystyle \mathbb {N} }
4935:96, March 2012, pp. 106-109.
4736:Salvatore Pincherle (1880).
4524:(3): 253–264. Archived from
4511:"Surds in Hindu mathematics"
3202:{\displaystyle \mathbb {Q} }
2866:{\displaystyle 3^{2n}=2^{m}}
2400:is not equal to 0 or 1, and
2322:to be the irrational number
2173:equation, the tail end of 10
1604:
1585:An irrational number may be
1524:{\displaystyle 2^{m}=3^{n}.}
474:by 2 yields an integer. Let
315:{\displaystyle \mathbb {Q} }
293:{\displaystyle \mathbb {R} }
271:{\displaystyle \mathbb {N} }
249:{\displaystyle \mathbb {Z} }
227:{\displaystyle \mathbb {Q} }
205:{\displaystyle \mathbb {R} }
7:
4885:. Blackwell. pp. 3–4.
4879:Philosophies of mathematics
4468:(1991). "China and India".
4340:Charles H. Edwards (1982).
3647:
3420:In constructive mathematics
2991:for some irrational number
2945:for some irrational number
2672:of positive integers. Then
2206:{\displaystyle 9990A=7155.}
1804:{\displaystyle a_{n}\neq 0}
1120:
897:. In the 10th century, the
629:The next step was taken by
166:countable, it follows that
151:), and in many other ways.
10:
6082:
4909:92, November 2008, p. 534.
4408:Bag, Amulya Kumar (1990).
3509:and every rational number
3176:{\displaystyle \{\pi ,e\}}
2823:{\displaystyle 3=2^{m/2n}}
2141:exactly. Here, both 10,000
2137:matches the tail end of 10
1303: 3 is irrational (log
173:
158:that the real numbers are
6025:
5967:
5893:
5873:Algebra of physical space
5795:
5703:
5574:
5376:
5312:
5301:
5099:
4805:(2–3). Teubner: 222–224.
4131:10.1017/S0025557200003193
3664:Diophantine approximation
3613:, the real numbers are a
3309:Euler–Mascheroni constant
3185:algebraically independent
3022:{\displaystyle n^{n^{n}}}
2984:{\displaystyle a^{a^{a}}}
2941:can be written either as
2371:Gelfond–Schneider theorem
2162:after the decimal point.
1965:greater than or equal to
1414:{\displaystyle 2^{m/n}=3}
879:Abū Kāmil Shujā ibn Aslam
147:(which in some cases are
5929:Extended complex numbers
5912:Extended natural numbers
5031:, Note IV, (1802), Paris
4707:Cajori, Florian (1928).
4606:University of St Andrews
4470:A History of Mathematics
4119:The Mathematical Gazette
3545:Since the reals form an
3426:constructive mathematics
3355:{\displaystyle ^{n}\pi }
3144:{\displaystyle m\pi +ne}
3029:for some natural number
2953:for some natural number
2169:equation from the 10,000
1580:
688:
661:to the second power and
349:isosceles right triangle
4742:Giornale di Matematiche
3410:{\displaystyle n>1.}
3323:{\displaystyle \gamma }
2365:= 2, which is rational.
1961:, there can never be a
1859:irrational numbers are
1751:where the coefficients
1103:Ferdinand von Lindemann
1059:Johann Heinrich Lambert
776:trigonometric functions
758:Madhava of Sangamagrama
524:in the first equation (
489:Squaring both sides of
5985:Transcendental numbers
5844:
5821:Hyperbolic quaternions
5767:
5728:
5690:
5662:
5634:
5606:
5529:
5494:
5461:
5433:
5405:
4769:(in French): 265–322.
3983:Dyadic (finite binary)
3897:
3859:
3821:
3783:
3745:
3607:
3541:Set of all irrationals
3523:
3503:
3483:
3447:
3411:
3385:
3356:
3324:
3298:
3203:
3177:
3145:
3113:
3087:
3086:{\displaystyle \pi -e}
3061:
3060:{\displaystyle \pi +e}
3023:
2985:
2935:
2867:
2824:
2780:
2716:
2655:
2510:
2472:
2259:
2207:
2124:
2067:
2019:
1841:is greater than 1. So
1805:
1772:
1742:
1525:
1479:
1415:
1368:
1297:proof by contradiction
1083:transcendental numbers
993:transcendental numbers
957:
871:
855:
543:Dividing by 2 yields 2
337:Hippasus of Metapontum
323:
316:
294:
272:
250:
228:
206:
44:
5917:Extended real numbers
5845:
5768:
5738:Split-complex numbers
5729:
5691:
5663:
5635:
5607:
5530:
5495:
5471:Constructible numbers
5462:
5434:
5406:
5029:Éléments de Géometrie
5025:Adrien-Marie Legendre
4995:Constructive Analysis
4970:John Wiley & Sons
4964:Mark Bridger (2007).
4798:Mathematische Annalen
4787:Gordan, Paul (1893).
4200:Annals of Mathematics
3898:
3860:
3822:
3784:
3746:
3669:Irrationality measure
3631:completely metrizable
3608:
3524:
3504:
3484:
3448:
3412:
3386:
3384:{\displaystyle ^{n}e}
3357:
3325:
3299:
3204:
3178:
3146:
3114:
3088:
3062:
3024:
2986:
2936:
2868:
2825:
2781:
2717:
2656:
2511:
2473:
2260:
2208:
2125:
2068:
2020:
1832:rational root theorem
1806:
1773:
1771:{\displaystyle a_{i}}
1743:
1526:
1480:
1416:
1369:
1246:quadratic irrationals
1075:Adrien-Marie Legendre
1053:Joseph-Louis Lagrange
1033:in the system of all
975:The 17th century saw
967:in the 13th century.
958:
867:
847:
842:quadratic irrationals
806:Muslim mathematicians
800:, the development of
720:Indian mathematicians
715:(800 BC or earlier).
317:
295:
273:
251:
229:
207:
181:
33:
6066:Sets of real numbers
5949:Supernatural numbers
5859:Multicomplex numbers
5832:
5816:Dual-complex numbers
5755:
5716:
5678:
5650:
5622:
5594:
5576:Composition algebras
5544:Arithmetical numbers
5515:
5482:
5449:
5421:
5393:
4932:Mathematical Gazette
4907:Mathematical Gazette
4628:Matvievskaya, Galina
4592:Robertson, Edmund F.
4556:Mathematics Magazine
4366:Mathematics Magazine
4101:Clifford A. Pickover
4028:Algebraic irrational
3881:
3843:
3805:
3767:
3729:
3702:Trigonometric number
3564:
3560:) distance function
3513:
3493:
3461:
3437:
3395:
3366:
3337:
3314:
3216:
3191:
3155:
3123:
3097:
3071:
3045:
2999:
2961:
2884:
2834:
2790:
2726:
2676:
2523:
2485:
2422:
2223:
2188:
2087:
2036:
1987:
1782:
1755:
1620:
1492:
1428:
1384:
1329:
1262:unique factorization
1149:improve this article
1101:transcendental, and
1097:(1873) first proved
1069:is rational (unless
983:, and especially of
928:
741:Mathematicians like
672:reductio ad absurdum
668:method of exhaustion
605:Greek mathematicians
558:is an integer, and 2
304:
282:
260:
238:
216:
194:
154:As a consequence of
5854:Split-biquaternions
5566:Eisenstein integers
5504:Closed-form numbers
4856:Scripta Mathematica
4744:: 178–254, 317–320.
4646:1987NYASA.500..253M
4590:O'Connor, John J.;
4173:. New York: Dover.
3719:
3212:It is not known if
3112:{\displaystyle m,n}
3041:It is not known if
2318:. Otherwise, take
1164:"Irrational number"
1049:Continued fractions
1041:(Crelle, 101), and
1023:Salvatore Pincherle
883:quadratic equations
732:Carl Benjamin Boyer
679:Theodorus of Cyrene
403:Pythagorean theorem
125:positional notation
102:, the golden ratio
6061:Irrational numbers
6012:Profinite integers
5975:Irrational numbers
5840:
5763:
5724:
5686:
5658:
5630:
5602:
5559:Gaussian rationals
5539:Computable numbers
5525:
5490:
5457:
5429:
5401:
5093:Irrational numbers
5054:2016-05-13 at the
4811:10.1007/bf01443647
4789:"Transcendenz von
4354:Kline 1990, p. 50.
4330:Kline 1990, p. 49.
4321:Kline 1990, p. 48.
4312:Kline 1990, p. 34.
4300:Kline 1990, p. 32.
3893:
3855:
3817:
3779:
3741:
3715:
3635:continued fraction
3603:
3519:
3499:
3479:
3443:
3407:
3381:
3352:
3320:
3305:Catalan's constant
3294:
3199:
3173:
3141:
3109:
3083:
3057:
3019:
2981:
2931:
2863:
2820:
2776:
2712:
2651:
2506:
2468:
2278:constructive proof
2255:
2203:
2120:
2063:
2015:
1949:is nonzero). When
1906:Decimal expansions
1801:
1768:
1738:
1521:
1475:
1411:
1364:
1017:(Annalen, 5), and
965:Leonardo Fibonacci
953:
470:is even, dividing
324:
312:
290:
268:
246:
224:
202:
120:, are irrational.
110:square root of two
53:irrational numbers
45:
18:Irrational numbers
6048:
6047:
5959:Superreal numbers
5939:Levi-Civita field
5934:Hyperreal numbers
5878:Spacetime algebra
5864:Geometric algebra
5777:Bicomplex numbers
5743:Split-quaternions
5584:Division algebras
5554:Gaussian integers
5476:Algebraic numbers
5379:definable numbers
5335:
5334:
5236:Supersilver ratio
5201:Supergolden ratio
5161:Twelfth root of 2
4979:978-1-470-45144-8
4180:978-0-486-60045-1
4082:
4081:
4078:
4077:
4074:
4073:
4070:
4069:
4059:
4058:
4055:
4054:
4051:
4050:
4047:
4046:
4035:Irrational period
4009:
4008:
4005:
4004:
4001:
4000:
3997:
3996:
3990:Repeating decimal
3957:
3956:
3953:
3952:
3948:Negative integers
3942:
3941:
3938:
3937:
3933:Composite numbers
3659:Computable number
3619:topological space
3617:and hence also a
3556:Under the usual (
3522:{\displaystyle q}
3502:{\displaystyle r}
3446:{\displaystyle r}
3281:
3273:
3263:
3247:
3230:
2668:, equals a ratio
2627:
2589:
2586:
2535:
2497:
2451:
2435:
2394:algebraic numbers
2272:Irrational powers
2253:
2240:
2181:leaving us with:
1978:repeating decimal
1778:are integers and
1611:algebraic numbers
1589:, that is a real
1573:Cases such as log
1359:
1225:
1224:
1217:
1199:
1065:is irrational if
1039:Leopold Kronecker
981:Abraham de Moivre
977:imaginary numbers
951:
810:algebraic objects
657:cubed instead of
631:Eudoxus of Cnidus
478:be this integer (
190:of real numbers (
16:(Redirected from
6073:
6038:
6037:
6005:
5995:
5907:Cardinal numbers
5868:Clifford algebra
5849:
5847:
5846:
5841:
5839:
5811:Dual quaternions
5772:
5770:
5769:
5764:
5762:
5733:
5731:
5730:
5725:
5723:
5695:
5693:
5692:
5687:
5685:
5667:
5665:
5664:
5659:
5657:
5639:
5637:
5636:
5631:
5629:
5611:
5609:
5608:
5603:
5601:
5534:
5532:
5531:
5526:
5524:
5523:
5499:
5497:
5496:
5491:
5489:
5466:
5464:
5463:
5458:
5456:
5443:Rational numbers
5438:
5436:
5435:
5430:
5428:
5410:
5408:
5407:
5402:
5400:
5362:
5355:
5348:
5339:
5338:
5307:
5295:
5285:
5273:Square root of 7
5268:Square root of 6
5263:
5246:Square root of 5
5241:
5231:Square root of 3
5226:
5216:
5206:
5196:Square root of 2
5189:
5174:
5156:
5124:
5109:
5086:
5079:
5072:
5063:
5062:
5013:
5012:
4990:
4984:
4983:
4961:
4955:
4953:
4951:
4942:
4936:
4919:
4910:
4903:
4897:
4896:
4884:
4873:
4867:
4863:
4851:
4845:
4844:
4829:
4823:
4822:
4784:
4778:
4777:
4775:
4764:
4752:
4746:
4745:
4733:
4727:
4720:
4714:
4712:
4704:
4698:
4696:
4673:
4667:
4665:
4624:
4611:
4609:
4587:
4581:
4580:
4547:
4541:
4540:
4538:
4536:
4530:
4515:
4506:
4500:
4499:
4462:
4456:
4454:
4428:
4422:
4421:
4405:
4399:
4397:
4361:
4355:
4352:
4346:
4345:
4337:
4331:
4328:
4322:
4319:
4313:
4310:
4301:
4298:
4292:
4282:
4276:
4275:
4239:
4233:
4232:
4191:
4185:
4184:
4157:
4151:
4150:
4125:(533): 327–330.
4110:
4104:
4094:
4024:
4023:
4015:
4014:
3972:
3971:
3963:
3962:
3906:
3905:
3902:
3900:
3899:
3894:
3892:
3872:
3871:
3868:
3867:
3864:
3862:
3861:
3856:
3854:
3834:
3833:
3830:
3829:
3826:
3824:
3823:
3818:
3816:
3796:
3795:
3792:
3791:
3788:
3786:
3785:
3780:
3778:
3758:
3757:
3754:
3753:
3750:
3748:
3747:
3742:
3740:
3720:
3714:
3711:
3710:
3707:
3706:
3697:Square root of 5
3692:Square root of 3
3686:
3677:
3642:zero-dimensional
3612:
3610:
3609:
3604:
3528:
3526:
3525:
3520:
3508:
3506:
3505:
3500:
3488:
3486:
3485:
3480:
3452:
3450:
3449:
3444:
3416:
3414:
3413:
3408:
3390:
3388:
3387:
3382:
3377:
3376:
3361:
3359:
3358:
3353:
3348:
3347:
3329:
3327:
3326:
3321:
3303:
3301:
3300:
3295:
3279:
3275:
3274:
3269:
3261:
3257:
3256:
3245:
3238:
3228:
3208:
3206:
3205:
3200:
3198:
3182:
3180:
3179:
3174:
3150:
3148:
3147:
3142:
3118:
3116:
3115:
3110:
3092:
3090:
3089:
3084:
3066:
3064:
3063:
3058:
3028:
3026:
3025:
3020:
3018:
3017:
3016:
3015:
2990:
2988:
2987:
2982:
2980:
2979:
2978:
2977:
2940:
2938:
2937:
2932:
2921:
2920:
2916:
2900:
2872:
2870:
2869:
2864:
2862:
2861:
2849:
2848:
2829:
2827:
2826:
2821:
2819:
2818:
2811:
2785:
2783:
2782:
2777:
2775:
2774:
2767:
2751:
2750:
2743:
2742:
2721:
2719:
2718:
2713:
2705:
2688:
2687:
2660:
2658:
2657:
2652:
2644:
2643:
2628:
2626:
2622:
2613:
2606:
2605:
2595:
2590:
2588:
2587:
2582:
2577:
2576:
2566:
2559:
2558:
2548:
2537:
2536:
2531:
2515:
2513:
2512:
2507:
2499:
2498:
2493:
2477:
2475:
2474:
2469:
2461:
2460:
2453:
2452:
2447:
2440:
2436:
2431:
2379:
2378:
2364:
2363:
2357:
2356:
2350:
2349:
2339:
2338:
2328:
2327:
2317:
2316:
2302:
2301:
2264:
2262:
2261:
2256:
2254:
2246:
2241:
2233:
2212:
2210:
2209:
2204:
2161:
2160:
2157:
2154:
2129:
2127:
2126:
2121:
2072:
2070:
2069:
2064:
2024:
2022:
2021:
2016:
1901:
1900:
1891:
1890:
1884:
1881: + 2,
1880:
1810:
1808:
1807:
1802:
1794:
1793:
1777:
1775:
1774:
1769:
1767:
1766:
1747:
1745:
1744:
1739:
1727:
1726:
1711:
1710:
1692:
1691:
1676:
1675:
1657:
1656:
1647:
1646:
1570: ≠ 0.
1530:
1528:
1527:
1522:
1517:
1516:
1504:
1503:
1484:
1482:
1481:
1476:
1474:
1473:
1461:
1460:
1451:
1450:
1446:
1420:
1418:
1417:
1412:
1404:
1403:
1399:
1377:It follows that
1373:
1371:
1370:
1365:
1360:
1352:
1341:
1340:
1280:
1275:
1268:there must be a
1234:square root of 2
1220:
1213:
1209:
1206:
1200:
1198:
1157:
1133:
1125:
1091:different method
1035:rational numbers
1019:Richard Dedekind
1010:Crelle's Journal
1001:Karl Weierstrass
962:
960:
959:
954:
952:
950:
941:
932:
916:specializing in
745:(in 628 AD) and
321:
319:
318:
313:
311:
299:
297:
296:
291:
289:
277:
275:
274:
269:
267:
255:
253:
252:
247:
245:
233:
231:
230:
225:
223:
211:
209:
208:
203:
201:
138:
134:
116:, other than of
94:
71:rational numbers
41:
40:
21:
6081:
6080:
6076:
6075:
6074:
6072:
6071:
6070:
6051:
6050:
6049:
6044:
6021:
6000:
5990:
5963:
5954:Surreal numbers
5944:Ordinal numbers
5889:
5835:
5833:
5830:
5829:
5791:
5758:
5756:
5753:
5752:
5750:
5748:Split-octonions
5719:
5717:
5714:
5713:
5705:
5699:
5681:
5679:
5676:
5675:
5653:
5651:
5648:
5647:
5625:
5623:
5620:
5619:
5616:Complex numbers
5597:
5595:
5592:
5591:
5570:
5519:
5518:
5516:
5513:
5512:
5485:
5483:
5480:
5479:
5452:
5450:
5447:
5446:
5424:
5422:
5419:
5418:
5396:
5394:
5391:
5390:
5387:Natural numbers
5372:
5366:
5336:
5331:
5308:
5299:
5293:
5283:
5262:
5254:
5239:
5224:
5214:
5204:
5187:
5169:
5154:
5122:
5107:
5095:
5090:
5056:Wayback Machine
5045:
5021:
5019:Further reading
5016:
5009:
4991:
4987:
4980:
4962:
4958:
4949:
4943:
4939:
4920:
4913:
4904:
4900:
4893:
4882:
4874:
4870:
4852:
4848:
4830:
4826:
4785:
4781:
4773:
4762:
4753:
4749:
4734:
4730:
4721:
4717:
4705:
4701:
4693:
4674:
4670:
4625:
4614:
4588:
4584:
4569:10.2307/2691411
4548:
4544:
4534:
4532:
4528:
4513:
4507:
4503:
4480:
4463:
4459:
4451:
4429:
4425:
4406:
4402:
4362:
4358:
4353:
4349:
4338:
4334:
4329:
4325:
4320:
4316:
4311:
4304:
4299:
4295:
4283:
4279:
4256:10.2307/3026893
4240:
4236:
4213:10.2307/1969021
4192:
4188:
4181:
4165:Philip Jourdain
4158:
4154:
4111:
4107:
4095:
4091:
4087:
3888:
3882:
3879:
3878:
3850:
3844:
3841:
3840:
3812:
3806:
3803:
3802:
3774:
3768:
3765:
3764:
3736:
3730:
3727:
3726:
3684:
3675:
3650:
3565:
3562:
3561:
3543:
3514:
3511:
3510:
3494:
3491:
3490:
3462:
3459:
3458:
3438:
3435:
3434:
3430:excluded middle
3422:
3396:
3393:
3392:
3372:
3369:
3367:
3364:
3363:
3343:
3340:
3338:
3335:
3334:
3315:
3312:
3311:
3268:
3264:
3252:
3248:
3234:
3217:
3214:
3213:
3194:
3192:
3189:
3188:
3156:
3153:
3152:
3124:
3121:
3120:
3098:
3095:
3094:
3072:
3069:
3068:
3046:
3043:
3042:
3039:
3011:
3007:
3006:
3002:
3000:
2997:
2996:
2973:
2969:
2968:
2964:
2962:
2959:
2958:
2912:
2908:
2904:
2896:
2885:
2882:
2881:
2857:
2853:
2841:
2837:
2835:
2832:
2831:
2807:
2803:
2799:
2791:
2788:
2787:
2763:
2759:
2755:
2738:
2734:
2733:
2729:
2727:
2724:
2723:
2701:
2683:
2679:
2677:
2674:
2673:
2639:
2635:
2618:
2614:
2601:
2597:
2596:
2594:
2581:
2572:
2568:
2567:
2554:
2550:
2549:
2547:
2530:
2526:
2524:
2521:
2520:
2492:
2488:
2486:
2483:
2482:
2446:
2442:
2441:
2430:
2426:
2425:
2423:
2420:
2419:
2376:
2374:
2361:
2359:
2354:
2352:
2347:
2345:
2336:
2334:
2325:
2323:
2314:
2312:
2299:
2297:
2274:
2245:
2232:
2224:
2221:
2220:
2189:
2186:
2185:
2158:
2155:
2152:
2150:
2088:
2085:
2084:
2037:
2034:
2033:
1988:
1985:
1984:
1908:
1898:
1896:
1888:
1886:
1882:
1878:
1863:. Examples are
1854:
1847:
1840:
1817:
1789:
1785:
1783:
1780:
1779:
1762:
1758:
1756:
1753:
1752:
1722:
1718:
1706:
1702:
1681:
1677:
1665:
1661:
1652:
1648:
1642:
1638:
1621:
1618:
1617:
1607:
1583:
1576:
1557:
1541:
1512:
1508:
1499:
1495:
1493:
1490:
1489:
1469:
1465:
1456:
1452:
1442:
1438:
1434:
1429:
1426:
1425:
1395:
1391:
1387:
1385:
1382:
1381:
1351:
1336:
1332:
1330:
1327:
1326:
1313:
1306:
1302:
1289:
1283:is irrational.
1278:
1273:
1254:
1242:perfect squares
1230:
1221:
1210:
1204:
1201:
1158:
1156:
1146:
1134:
1123:
1095:Charles Hermite
989:complex numbers
973:
942:
933:
931:
929:
926:
925:
794:
766:infinite series
764:discovered the
691:
329:
307:
305:
302:
301:
285:
283:
280:
279:
263:
261:
258:
257:
241:
239:
236:
235:
219:
217:
214:
213:
197:
195:
192:
191:
176:
136:
132:
118:perfect squares
114:natural numbers
92:
84:incommensurable
38:
36:
28:
23:
22:
15:
12:
11:
5:
6079:
6069:
6068:
6063:
6046:
6045:
6043:
6042:
6032:
6030:Classification
6026:
6023:
6022:
6020:
6019:
6017:Normal numbers
6014:
6009:
5987:
5982:
5977:
5971:
5969:
5965:
5964:
5962:
5961:
5956:
5951:
5946:
5941:
5936:
5931:
5926:
5925:
5924:
5914:
5909:
5903:
5901:
5899:infinitesimals
5891:
5890:
5888:
5887:
5886:
5885:
5880:
5875:
5861:
5856:
5851:
5838:
5823:
5818:
5813:
5808:
5802:
5800:
5793:
5792:
5790:
5789:
5784:
5779:
5774:
5761:
5745:
5740:
5735:
5722:
5709:
5707:
5701:
5700:
5698:
5697:
5684:
5669:
5656:
5641:
5628:
5613:
5600:
5580:
5578:
5572:
5571:
5569:
5568:
5563:
5562:
5561:
5551:
5546:
5541:
5536:
5522:
5506:
5501:
5488:
5473:
5468:
5455:
5440:
5427:
5412:
5399:
5383:
5381:
5374:
5373:
5365:
5364:
5357:
5350:
5342:
5333:
5332:
5330:
5329:
5324:
5322:Transcendental
5319:
5313:
5310:
5309:
5302:
5300:
5298:
5297:
5287:
5276:
5275:
5270:
5265:
5258:
5248:
5243:
5233:
5228:
5218:
5208:
5198:
5192:
5191:
5181:
5179:Cube root of 2
5176:
5163:
5158:
5148:
5143:
5141:Logarithm of 2
5137:
5136:
5131:
5126:
5116:
5111:
5100:
5097:
5096:
5089:
5088:
5081:
5074:
5066:
5060:
5059:
5044:
5043:External links
5041:
5040:
5039:
5032:
5020:
5017:
5015:
5014:
5007:
4985:
4978:
4956:
4945:Albert, John.
4937:
4911:
4898:
4891:
4868:
4846:
4824:
4779:
4756:Lambert, J. H.
4747:
4728:
4715:
4699:
4691:
4668:
4640:(1): 253–277.
4612:
4582:
4563:(3): 163–174.
4542:
4501:
4478:
4457:
4449:
4433:Selin, Helaine
4423:
4400:
4372:(4): 201–203.
4356:
4347:
4332:
4323:
4314:
4302:
4293:
4277:
4250:(5): 312–316.
4234:
4207:(2): 242–264.
4195:Kurt Von Fritz
4186:
4179:
4152:
4105:
4088:
4086:
4083:
4080:
4079:
4076:
4075:
4072:
4071:
4068:
4067:
4061:
4060:
4057:
4056:
4053:
4052:
4049:
4048:
4045:
4044:
4042:Transcendental
4038:
4037:
4031:
4030:
4021:
4011:
4010:
4007:
4006:
4003:
4002:
3999:
3998:
3995:
3994:
3992:
3986:
3985:
3979:
3978:
3976:Finite decimal
3969:
3959:
3958:
3955:
3954:
3951:
3950:
3944:
3943:
3940:
3939:
3936:
3935:
3929:
3928:
3922:
3921:
3914:
3913:
3903:
3891:
3886:
3865:
3853:
3848:
3827:
3815:
3810:
3789:
3777:
3772:
3751:
3739:
3734:
3717:Number systems
3705:
3704:
3699:
3694:
3689:
3680:
3671:
3666:
3661:
3656:
3649:
3646:
3602:
3599:
3596:
3593:
3590:
3587:
3584:
3581:
3578:
3575:
3572:
3569:
3542:
3539:
3518:
3498:
3478:
3475:
3472:
3469:
3466:
3442:
3421:
3418:
3406:
3403:
3400:
3380:
3375:
3371:
3351:
3346:
3342:
3319:
3293:
3290:
3287:
3284:
3278:
3272:
3267:
3260:
3255:
3251:
3244:
3241:
3237:
3233:
3227:
3224:
3221:
3197:
3172:
3169:
3166:
3163:
3160:
3140:
3137:
3134:
3131:
3128:
3108:
3105:
3102:
3082:
3079:
3076:
3056:
3053:
3050:
3038:
3037:Open questions
3035:
3014:
3010:
3005:
2976:
2972:
2967:
2930:
2927:
2924:
2919:
2915:
2911:
2907:
2903:
2899:
2895:
2892:
2889:
2860:
2856:
2852:
2847:
2844:
2840:
2817:
2814:
2810:
2806:
2802:
2798:
2795:
2773:
2770:
2766:
2762:
2758:
2754:
2749:
2746:
2741:
2737:
2732:
2711:
2708:
2704:
2700:
2697:
2694:
2691:
2686:
2682:
2662:
2661:
2650:
2647:
2642:
2638:
2634:
2631:
2625:
2621:
2617:
2612:
2609:
2604:
2600:
2593:
2585:
2580:
2575:
2571:
2565:
2562:
2557:
2553:
2546:
2543:
2540:
2534:
2529:
2505:
2502:
2496:
2491:
2479:
2478:
2467:
2464:
2459:
2456:
2450:
2445:
2439:
2434:
2429:
2382:transcendental
2367:
2366:
2273:
2270:
2266:
2265:
2252:
2249:
2244:
2239:
2236:
2231:
2228:
2214:
2213:
2202:
2199:
2196:
2193:
2131:
2130:
2119:
2115:
2111:
2107:
2104:
2101:
2098:
2095:
2092:
2074:
2073:
2062:
2058:
2054:
2050:
2047:
2044:
2041:
2026:
2025:
2014:
2010:
2006:
2002:
1998:
1995:
1992:
1907:
1904:
1861:transcendental
1853:
1852:Transcendental
1850:
1845:
1838:
1826: − 2
1815:
1800:
1797:
1792:
1788:
1765:
1761:
1749:
1748:
1737:
1733:
1730:
1725:
1721:
1717:
1714:
1709:
1705:
1701:
1698:
1695:
1690:
1687:
1684:
1680:
1674:
1671:
1668:
1664:
1660:
1655:
1651:
1645:
1641:
1637:
1634:
1631:
1628:
1625:
1606:
1603:
1599:transcendental
1582:
1579:
1574:
1555:
1539:
1532:
1531:
1520:
1515:
1511:
1507:
1502:
1498:
1486:
1485:
1472:
1468:
1464:
1459:
1455:
1449:
1445:
1441:
1437:
1433:
1422:
1421:
1410:
1407:
1402:
1398:
1394:
1390:
1375:
1374:
1363:
1358:
1355:
1350:
1347:
1344:
1339:
1335:
1311:
1304:
1300:
1288:
1285:
1253:
1250:
1229:
1226:
1223:
1222:
1137:
1135:
1128:
1122:
1119:
985:Leonhard Euler
972:
969:
949:
945:
940:
936:
877:mathematician
836:mathematician
793:
790:
690:
687:
624:four paradoxes
602:
601:
582:
571:
552:
541:
516:Substituting 4
514:
487:
464:
453:
438:
399:
380:
328:
327:Ancient Greece
325:
310:
288:
266:
244:
222:
200:
175:
172:
156:Cantor's proof
65:) are all the
43:is irrational.
26:
9:
6:
4:
3:
2:
6078:
6067:
6064:
6062:
6059:
6058:
6056:
6041:
6033:
6031:
6028:
6027:
6024:
6018:
6015:
6013:
6010:
6007:
6003:
5997:
5993:
5988:
5986:
5983:
5981:
5980:Fuzzy numbers
5978:
5976:
5973:
5972:
5970:
5966:
5960:
5957:
5955:
5952:
5950:
5947:
5945:
5942:
5940:
5937:
5935:
5932:
5930:
5927:
5923:
5920:
5919:
5918:
5915:
5913:
5910:
5908:
5905:
5904:
5902:
5900:
5896:
5892:
5884:
5881:
5879:
5876:
5874:
5871:
5870:
5869:
5865:
5862:
5860:
5857:
5855:
5852:
5827:
5824:
5822:
5819:
5817:
5814:
5812:
5809:
5807:
5804:
5803:
5801:
5799:
5794:
5788:
5785:
5783:
5782:Biquaternions
5780:
5778:
5775:
5749:
5746:
5744:
5741:
5739:
5736:
5711:
5710:
5708:
5702:
5673:
5670:
5645:
5642:
5617:
5614:
5589:
5585:
5582:
5581:
5579:
5577:
5573:
5567:
5564:
5560:
5557:
5556:
5555:
5552:
5550:
5547:
5545:
5542:
5540:
5537:
5510:
5507:
5505:
5502:
5477:
5474:
5472:
5469:
5444:
5441:
5416:
5413:
5388:
5385:
5384:
5382:
5380:
5375:
5370:
5363:
5358:
5356:
5351:
5349:
5344:
5343:
5340:
5328:
5327:Trigonometric
5325:
5323:
5320:
5318:
5317:Schizophrenic
5315:
5314:
5311:
5306:
5291:
5288:
5281:
5278:
5277:
5274:
5271:
5269:
5266:
5261:
5257:
5252:
5249:
5247:
5244:
5237:
5234:
5232:
5229:
5222:
5219:
5212:
5211:Erdős–Borwein
5209:
5202:
5199:
5197:
5194:
5193:
5185:
5184:Plastic ratio
5182:
5180:
5177:
5172:
5167:
5164:
5162:
5159:
5152:
5149:
5147:
5144:
5142:
5139:
5138:
5135:
5132:
5130:
5127:
5120:
5117:
5115:
5112:
5105:
5102:
5101:
5098:
5094:
5087:
5082:
5080:
5075:
5073:
5068:
5067:
5064:
5057:
5053:
5050:
5047:
5046:
5037:
5033:
5030:
5026:
5023:
5022:
5010:
5008:0-387-15066-8
5004:
5000:
4996:
4989:
4981:
4975:
4971:
4967:
4960:
4948:
4941:
4934:
4933:
4929:irrational",
4928:
4924:
4918:
4916:
4908:
4902:
4894:
4892:0-631-19544-0
4888:
4881:
4880:
4872:
4866:
4861:
4857:
4850:
4843:
4839:
4836:(10): 45–61,
4835:
4828:
4820:
4816:
4812:
4808:
4804:
4800:
4799:
4794:
4792:
4783:
4772:
4768:
4761:
4757:
4751:
4743:
4739:
4732:
4725:
4719:
4710:
4703:
4694:
4692:1-4020-0260-2
4688:
4684:
4680:
4672:
4663:
4659:
4655:
4651:
4647:
4643:
4639:
4635:
4634:
4629:
4623:
4621:
4619:
4617:
4607:
4603:
4602:
4597:
4593:
4586:
4578:
4574:
4570:
4566:
4562:
4558:
4557:
4552:
4546:
4531:on 2018-10-03
4527:
4523:
4519:
4512:
4505:
4498:
4495:
4489:
4485:
4481:
4475:
4471:
4467:
4461:
4452:
4450:1-4020-0260-2
4446:
4442:
4438:
4434:
4427:
4419:
4415:
4411:
4404:
4395:
4391:
4387:
4383:
4379:
4375:
4371:
4367:
4360:
4351:
4343:
4336:
4327:
4318:
4309:
4307:
4297:
4290:
4286:
4281:
4273:
4269:
4265:
4261:
4257:
4253:
4249:
4245:
4238:
4230:
4226:
4222:
4218:
4214:
4210:
4206:
4202:
4201:
4196:
4190:
4182:
4176:
4172:
4171:
4166:
4162:
4161:Cantor, Georg
4156:
4148:
4144:
4140:
4136:
4132:
4128:
4124:
4120:
4116:
4109:
4102:
4098:
4093:
4089:
4066:
4063:
4062:
4043:
4040:
4039:
4036:
4033:
4032:
4029:
4026:
4025:
4022:
4020:
4017:
4016:
4013:
4012:
3993:
3991:
3988:
3987:
3984:
3981:
3980:
3977:
3974:
3973:
3970:
3968:
3965:
3964:
3961:
3960:
3949:
3946:
3945:
3934:
3931:
3930:
3927:
3926:Prime numbers
3924:
3923:
3919:
3916:
3915:
3911:
3908:
3907:
3904:
3884:
3877:
3874:
3873:
3870:
3869:
3866:
3846:
3839:
3836:
3835:
3832:
3831:
3828:
3808:
3801:
3798:
3797:
3794:
3793:
3790:
3770:
3763:
3760:
3759:
3756:
3755:
3752:
3732:
3725:
3722:
3721:
3718:
3713:
3712:
3709:
3708:
3703:
3700:
3698:
3695:
3693:
3690:
3688:
3687:is irrational
3681:
3679:
3678:is irrational
3672:
3670:
3667:
3665:
3662:
3660:
3657:
3655:
3654:Brjuno number
3652:
3651:
3645:
3643:
3638:
3636:
3632:
3628:
3624:
3620:
3616:
3597:
3594:
3591:
3585:
3579:
3576:
3573:
3567:
3559:
3554:
3552:
3548:
3538:
3536:
3532:
3531:Errett Bishop
3516:
3496:
3473:
3470:
3467:
3456:
3440:
3431:
3427:
3417:
3404:
3401:
3398:
3378:
3373:
3370:
3349:
3344:
3341:
3333:
3317:
3310:
3306:
3291:
3288:
3285:
3282:
3276:
3270:
3265:
3258:
3253:
3249:
3242:
3239:
3235:
3231:
3225:
3222:
3219:
3210:
3186:
3167:
3164:
3161:
3138:
3135:
3132:
3129:
3126:
3106:
3103:
3100:
3080:
3077:
3074:
3054:
3051:
3048:
3034:
3032:
3012:
3008:
3003:
2994:
2974:
2970:
2965:
2956:
2952:
2948:
2944:
2922:
2917:
2913:
2909:
2901:
2897:
2893:
2878:
2876:
2858:
2854:
2850:
2845:
2842:
2838:
2815:
2812:
2808:
2804:
2800:
2796:
2793:
2771:
2768:
2764:
2760:
2756:
2752:
2747:
2744:
2739:
2735:
2730:
2709:
2706:
2702:
2698:
2695:
2692:
2689:
2684:
2680:
2671:
2667:
2666:contradiction
2648:
2645:
2640:
2636:
2632:
2629:
2623:
2619:
2615:
2610:
2607:
2602:
2598:
2591:
2583:
2578:
2573:
2569:
2563:
2560:
2555:
2551:
2544:
2541:
2538:
2532:
2527:
2519:
2518:
2517:
2503:
2500:
2494:
2489:
2465:
2462:
2457:
2454:
2448:
2443:
2437:
2432:
2427:
2418:
2417:
2416:
2413:
2411:
2407:
2403:
2399:
2395:
2391:
2387:
2383:
2372:
2343:
2332:
2321:
2310:
2306:
2295:
2294:
2293:
2292:is rational:
2291:
2287:
2283:
2279:
2269:
2250:
2247:
2242:
2237:
2234:
2229:
2226:
2219:
2218:
2217:
2200:
2197:
2194:
2191:
2184:
2183:
2182:
2180:
2176:
2172:
2168:
2163:
2148:
2144:
2140:
2136:
2117:
2113:
2109:
2105:
2102:
2099:
2096:
2093:
2090:
2083:
2082:
2081:
2079:
2060:
2056:
2052:
2048:
2045:
2042:
2039:
2032:
2031:
2030:
2012:
2008:
2004:
2000:
1996:
1993:
1990:
1983:
1982:
1981:
1979:
1974:
1972:
1968:
1964:
1960:
1956:
1952:
1951:long division
1948:
1944:
1940:
1935:
1933:
1929:
1926:
1922:
1918:
1914:
1903:
1895:
1885: +
1876:
1871:
1870:
1866:
1862:
1858:
1849:
1844:
1837:
1833:
1829:
1825:
1821:
1814:
1798:
1795:
1790:
1786:
1763:
1759:
1735:
1731:
1728:
1723:
1719:
1715:
1712:
1707:
1703:
1699:
1696:
1693:
1688:
1685:
1682:
1678:
1672:
1669:
1666:
1662:
1658:
1653:
1649:
1643:
1639:
1635:
1629:
1623:
1616:
1615:
1614:
1612:
1602:
1600:
1596:
1592:
1588:
1578:
1571:
1569:
1565:
1561:
1553:
1549:
1545:
1537:
1536:prime factors
1518:
1513:
1509:
1505:
1500:
1496:
1488:
1487:
1470:
1466:
1462:
1457:
1447:
1443:
1439:
1435:
1424:
1423:
1408:
1405:
1400:
1396:
1392:
1388:
1380:
1379:
1378:
1361:
1356:
1353:
1348:
1345:
1342:
1337:
1333:
1325:
1324:
1323:
1321:
1317:
1308:
1298:
1294:
1284:
1282:
1271:
1267:
1263:
1259:
1252:General roots
1249:
1247:
1243:
1239:
1235:
1219:
1216:
1208:
1197:
1194:
1190:
1187:
1183:
1180:
1176:
1173:
1169:
1166: –
1165:
1161:
1160:Find sources:
1154:
1150:
1144:
1143:
1138:This article
1136:
1132:
1127:
1126:
1118:
1116:
1112:
1111:Adolf Hurwitz
1108:
1107:David Hilbert
1104:
1100:
1096:
1092:
1088:
1084:
1080:
1076:
1072:
1068:
1064:
1060:
1056:
1054:
1050:
1046:
1044:
1043:Charles Méray
1040:
1036:
1032:
1031:cut (Schnitt)
1028:
1024:
1020:
1016:
1012:
1011:
1006:
1002:
998:
994:
990:
986:
982:
978:
971:Modern period
968:
966:
947:
943:
938:
934:
923:
919:
915:
911:
907:
902:
900:
896:
892:
888:
884:
880:
876:
870:
866:
864:
860:
854:
852:
846:
843:
839:
835:
831:
827:
823:
819:
815:
811:
807:
803:
799:
792:Islamic World
789:
787:
786:
781:
777:
773:
772:
767:
763:
759:
754:
752:
748:
744:
739:
735:
733:
729:
725:
721:
716:
714:
713:
712:Shulba Sutras
708:
707:
702:
701:
696:
686:
684:
680:
676:
673:
669:
664:
660:
656:
652:
648:
644:
638:
636:
632:
627:
625:
621:
617:
612:
610:
606:
599:
595:
591:
587:
583:
581:must be even.
580:
576:
572:
569:
565:
561:
557:
553:
550:
546:
542:
539:
535:
531:
527:
523:
519:
515:
512:
508:
504:
500:
496:
492:
488:
485:
481:
477:
473:
469:
465:
463:must be even.
462:
458:
454:
451:
447:
443:
439:
436:
432:
428:
424:
420:
416:
412:
408:
404:
400:
397:
393:
389:
385:
381:
378:
374:
370:
366:
362:
358:
357:
356:
354:
353:commensurable
350:
346:
342:
338:
334:
189:
185:
184:Euler diagram
180:
171:
169:
165:
161:
157:
152:
150:
146:
141:
130:
126:
121:
119:
115:
111:
107:
106:
101:
100:
95:
88:
86:
85:
80:
76:
72:
69:that are not
68:
64:
60:
59:
54:
50:
42:
32:
19:
6001:
5991:
5974:
5806:Dual numbers
5798:hypercomplex
5588:Real numbers
5259:
5255:
5251:Silver ratio
5221:Golden ratio
5170:
5092:
5035:
5028:
4994:
4988:
4965:
4959:
4940:
4930:
4926:
4922:
4906:
4901:
4878:
4871:
4859:
4855:
4849:
4833:
4827:
4802:
4796:
4790:
4782:
4766:
4750:
4741:
4731:
4718:
4708:
4702:
4678:
4671:
4637:
4631:
4599:
4585:
4560:
4554:
4545:
4535:18 September
4533:. Retrieved
4526:the original
4521:
4517:
4504:
4493:
4491:
4469:
4460:
4436:
4426:
4417:
4413:
4403:
4369:
4365:
4359:
4350:
4341:
4335:
4326:
4317:
4296:
4288:
4280:
4247:
4243:
4237:
4204:
4198:
4189:
4169:
4155:
4122:
4118:
4108:
4092:
4018:
3639:
3615:metric space
3555:
3544:
3423:
3211:
3040:
3030:
2992:
2954:
2950:
2946:
2942:
2879:
2669:
2663:
2480:
2414:
2405:
2401:
2397:
2389:
2385:
2368:
2341:
2330:
2319:
2308:
2304:
2289:
2288:, such that
2285:
2281:
2275:
2267:
2215:
2178:
2174:
2170:
2166:
2164:
2146:
2142:
2138:
2134:
2132:
2077:
2075:
2027:
1975:
1970:
1966:
1958:
1954:
1946:
1942:
1938:
1936:
1909:
1893:
1872:
1868:
1864:
1855:
1842:
1835:
1827:
1823:
1819:
1812:
1750:
1608:
1584:
1572:
1567:
1563:
1559:
1551:
1547:
1543:
1533:
1376:
1319:
1315:
1309:
1295:. Here is a
1290:
1266:lowest terms
1255:
1238:golden ratio
1231:
1228:Square roots
1211:
1202:
1192:
1185:
1178:
1171:
1159:
1147:Please help
1142:verification
1139:
1098:
1087:Georg Cantor
1070:
1066:
1062:
1057:
1047:
1027:Paul Tannery
1015:Georg Cantor
1008:
1005:Eduard Heine
974:
903:
895:fourth roots
887:coefficients
872:
868:
863:arithmetical
856:
850:
848:
829:
822:real numbers
809:
795:
783:
769:
755:
740:
736:
728:square roots
717:
710:
704:
698:
695:Vedic period
692:
677:
670:, a kind of
662:
658:
654:
653:squared and
650:
646:
642:
639:
628:
616:Zeno of Elea
613:
608:
603:
597:
593:
589:
585:
578:
574:
567:
563:
559:
555:
548:
544:
537:
533:
532:) gives us 4
529:
525:
521:
517:
510:
506:
502:
498:
494:
490:
483:
479:
475:
471:
467:
460:
456:
449:
445:
441:
434:
430:
426:
422:
418:
414:
410:
406:
395:
391:
387:
383:
376:
372:
368:
364:
360:
330:
186:showing the
153:
142:
122:
104:
98:
89:
82:
67:real numbers
62:
56:
52:
46:
5968:Other types
5787:Bioctonions
5644:Quaternions
4724:Cajori 1928
4551:Katz, V. J.
4344:. Springer.
3683:Proof that
3674:Proof that
3627:G-delta set
3625:. Being a
3547:uncountable
2373:shows that
1921:hexadecimal
1115:Paul Gordan
798:Middle Ages
780:Jyeṣṭhadeva
751:Bhāskara II
743:Brahmagupta
351:was indeed
333:Pythagorean
160:uncountable
77:. When the
49:mathematics
34:The number
6055:Categories
5922:Projective
5895:Infinities
5151:Lemniscate
4494:Sulbasutra
4479:0471093742
4085:References
4019:Irrational
3332:tetrations
2412:is used).
1925:positional
1857:Almost all
1595:polynomial
1322:, we have
1310:Assume log
1293:logarithms
1287:Logarithms
1175:newspapers
922:numerators
859:cube roots
785:Yuktibhāṣā
747:Bhāskara I
709:, and the
345:hypotenuse
335:(possibly
168:almost all
108:, and the
6006:solenoids
5826:Sedenions
5672:Octonions
5114:Liouville
5104:Chaitin's
4819:123203471
4662:121416910
4497:concepts.
4394:124565880
4285:Kline, M.
4272:115390951
4229:126296119
4163:(1955) .
4147:123995083
4139:0025-5572
4065:Imaginary
3595:−
3558:Euclidean
3551:countable
3471:−
3350:π
3318:γ
3307:, or the
3289:π
3286:
3266:π
3250:π
3232:π
3220:π
3162:π
3130:π
3078:−
3075:π
3049:π
2926:∞
2745:
2690:
2646:
2608:
2579:
2561:
2539:
2501:
2455:
2392:are both
2296:Consider
2118:…
2061:…
2013:…
1963:remainder
1796:≠
1697:⋯
1686:−
1670:−
1609:The real
1605:Algebraic
1587:algebraic
1343:
910:Al-Hassār
838:Al-Mahani
818:magnitude
706:Brahmanas
577:is even,
459:is even,
341:pentagram
164:rationals
5415:Integers
5377:Sets of
5052:Archived
4999:Springer
4771:Archived
4758:(1761).
4726:, pg.89)
4713:pg. 269.
4683:Springer
4594:(1999).
4441:Springer
4287:(1990).
3967:Fraction
3800:Rational
3648:See also
3623:complete
3489:between
2340:. Then
1928:notation
1875:subfield
1299:that log
1205:May 2023
1121:Examples
891:equation
875:Egyptian
830:Elements
760:and the
700:Samhitas
620:infinite
162:and the
149:periodic
75:integers
63:rational
5996:numbers
5828: (
5674: (
5646: (
5618: (
5590: (
5511: (
5509:Periods
5478: (
5445: (
5417: (
5389: (
5371:systems
5280:Euler's
5166:Apéry's
4842:1891736
4642:Bibcode
4577:2691411
4386:2690123
4264:3026893
4221:1969021
4167:(ed.).
3876:Natural
3838:Integer
3724:Complex
2375:√
2360:√
2353:√
2346:√
2335:√
2324:√
2313:√
2298:√
2110:162.162
1945:(where
1934:bases.
1932:natural
1897:√
1887:√
1281:th root
1189:scholar
1013:, 74),
834:Persian
816:" and "
802:algebra
796:In the
635:Eudoxus
497:yields
401:By the
382:Assume
174:History
37:√
5796:Other
5369:Number
5146:Dottie
5005:
4976:
4889:
4862:: 229.
4840:
4834:Neusis
4817:
4793:und π"
4689:
4660:
4575:
4488:414892
4486:
4476:
4447:
4392:
4384:
4270:
4262:
4227:
4219:
4177:
4145:
4137:
3685:π
3280:
3262:
3246:
3229:
2995:or as
2949:or as
2830:hence
2786:hence
2722:hence
2396:, and
2145:and 10
1913:binary
1191:
1184:
1177:
1170:
1162:
997:Euclid
889:in an
885:or as
832:, the
826:ratios
814:number
724:Manava
609:alogos
573:Since
554:Since
505:), or
466:Since
455:Since
440:Since
390:, and
367:, and
347:of an
51:, the
6004:-adic
5994:-adic
5751:Over
5712:Over
5706:types
5704:Split
5134:Cahen
5129:Omega
5119:Prime
4950:(PDF)
4925:with
4883:(PDF)
4815:S2CID
4774:(PDF)
4763:(PDF)
4658:S2CID
4573:JSTOR
4529:(PDF)
4514:(PDF)
4466:Boyer
4390:S2CID
4382:JSTOR
4268:S2CID
4260:JSTOR
4225:S2CID
4217:JSTOR
4143:S2CID
4099:. by
3455:apart
3187:over
2216:Then
2201:7155.
2149:have
2049:7.162
1930:with
1917:octal
1593:of a
1581:Types
1566:with
1550:with
1270:prime
1196:JSTOR
1182:books
899:Iraqi
689:India
683:surds
79:ratio
6040:List
5897:and
5003:ISBN
4974:ISBN
4887:ISBN
4865:copy
4687:ISBN
4537:2018
4484:OCLC
4474:ISBN
4445:ISBN
4175:ISBN
4135:ISSN
3920:: 1
3912:: 0
3910:Zero
3762:Real
3402:>
3067:(or
2388:and
2351:) =
2329:and
2284:and
2238:9990
2235:7155
2192:9990
2151:.162
1892:and
1591:root
1318:and
1232:The
1168:news
1113:and
873:The
851:etc.
645:and
596:and
588:and
520:for
501:= (2
396:i.e.
5173:(3)
4807:doi
4650:doi
4638:500
4565:doi
4374:doi
4252:doi
4209:doi
4127:doi
3918:One
3533:'s
3424:In
3362:or
3183:is
2736:log
2681:log
2670:m/n
2637:log
2599:log
2570:log
2552:log
2528:log
2490:log
2444:log
2380:is
2344:= (
2159:...
2156:162
2153:162
2114:162
2097:000
2057:162
2053:162
2009:162
2005:162
2001:162
1997:0.7
1957:by
1941:by
1919:or
1334:log
1151:by
914:Fez
804:by
649:as
536:= 2
528:= 2
509:= 4
493:= 2
482:= 2
444:= 2
425:= 2
188:set
182:An
58:in-
47:In
6057::
5586::
5290:Pi
5027:,
5001:.
4997:.
4972:.
4968:.
4914:^
4860:19
4858:.
4838:MR
4813:.
4803:43
4801:.
4795:.
4765:.
4740:.
4685:.
4681:.
4656:.
4648:.
4636:.
4615:^
4604:.
4598:.
4571:.
4561:63
4559:.
4522:28
4520:.
4516:.
4490:.
4482:.
4443:.
4439:.
4418:25
4416:.
4412:.
4388:.
4380:.
4370:49
4368:.
4305:^
4266:.
4258:.
4248:11
4246:.
4223:.
4215:.
4205:46
4203:.
4141:.
4133:.
4123:95
4121:.
4117:.
3644:.
3537:.
3428:,
3405:1.
3283:ln
3209:.
3033:.
2466:3.
2358:=
2333:=
2311:=
2307:=
2251:74
2248:53
2091:10
2040:10
1915:,
1869:r.
1601:.
1575:10
1248:.
1117:.
1045:.
908:.
788:.
778:.
703:,
566:,
562:=
547:=
486:).
448:,
437:).
433:=
417:=
409:=
405::
386:,
363:,
322:).
61:+
6008:)
6002:p
5998:(
5992:p
5866:/
5850:)
5837:S
5773::
5760:C
5734::
5721:R
5696:)
5683:O
5668:)
5655:H
5640:)
5627:C
5612:)
5599:R
5535:)
5521:P
5500:)
5487:A
5467:)
5454:Q
5439:)
5426:Z
5411:)
5398:N
5361:e
5354:t
5347:v
5296:)
5294:π
5292:(
5286:)
5284:e
5282:(
5264:)
5260:S
5256:δ
5253:(
5242:)
5240:ς
5238:(
5227:)
5225:φ
5223:(
5217:)
5215:E
5213:(
5207:)
5205:ψ
5203:(
5190:)
5188:ρ
5186:(
5175:)
5171:ζ
5168:(
5157:)
5155:ϖ
5153:(
5125:)
5123:ρ
5121:(
5110:)
5108:Ω
5106:(
5085:e
5078:t
5071:v
5011:.
4982:.
4927:a
4923:a
4895:.
4821:.
4809::
4791:e
4722:(
4697:.
4695:.
4664:.
4652::
4644::
4610:.
4608:.
4579:.
4567::
4539:.
4455:.
4453:.
4420:.
4398:.
4396:.
4376::
4274:.
4254::
4231:.
4211::
4183:.
4149:.
4129::
3890:N
3885::
3852:Z
3847::
3814:Q
3809::
3776:R
3771::
3738:C
3733::
3676:e
3601:|
3598:y
3592:x
3589:|
3586:=
3583:)
3580:y
3577:,
3574:x
3571:(
3568:d
3517:q
3497:r
3477:|
3474:q
3468:r
3465:|
3441:r
3399:n
3379:e
3374:n
3345:n
3292:,
3277:,
3271:2
3259:,
3254:e
3243:,
3240:e
3236:/
3226:,
3223:e
3196:Q
3171:}
3168:e
3165:,
3159:{
3139:e
3136:n
3133:+
3127:m
3107:n
3104:,
3101:m
3081:e
3055:e
3052:+
3031:n
3013:n
3009:n
3004:n
2993:a
2975:a
2971:a
2966:a
2955:n
2951:n
2947:a
2943:a
2929:)
2923:,
2918:e
2914:/
2910:1
2906:)
2902:e
2898:/
2894:1
2891:(
2888:(
2859:m
2855:2
2851:=
2846:n
2843:2
2839:3
2816:n
2813:2
2809:/
2805:m
2801:2
2797:=
2794:3
2772:n
2769:2
2765:/
2761:m
2757:2
2753:=
2748:3
2740:2
2731:2
2710:n
2707:2
2703:/
2699:m
2696:=
2693:3
2685:2
2649:3
2641:2
2633:2
2630:=
2624:2
2620:/
2616:1
2611:3
2603:2
2592:=
2584:2
2574:2
2564:3
2556:2
2545:=
2542:3
2533:2
2504:3
2495:2
2463:=
2458:3
2449:2
2438:)
2433:2
2428:(
2406:a
2402:b
2398:a
2390:b
2386:a
2377:2
2362:2
2355:2
2348:2
2342:a
2337:2
2331:b
2326:2
2320:a
2315:2
2309:b
2305:a
2300:2
2290:a
2286:b
2282:a
2243:=
2230:=
2227:A
2198:=
2195:A
2179:A
2175:A
2171:A
2167:A
2147:A
2143:A
2139:A
2135:A
2106:7
2103:=
2100:A
2094:,
2078:r
2046:=
2043:A
1994:=
1991:A
1971:m
1967:m
1959:m
1955:n
1947:m
1943:m
1939:n
1899:3
1894:e
1889:2
1883:π
1879:π
1865:e
1846:0
1843:x
1839:0
1836:x
1828:x
1824:x
1820:x
1816:0
1813:x
1799:0
1791:n
1787:a
1764:i
1760:a
1736:,
1732:0
1729:=
1724:0
1720:a
1716:+
1713:x
1708:1
1704:a
1700:+
1694:+
1689:1
1683:n
1679:x
1673:1
1667:n
1663:a
1659:+
1654:n
1650:x
1644:n
1640:a
1636:=
1633:)
1630:x
1627:(
1624:p
1568:n
1564:n
1562:/
1560:m
1556:2
1552:n
1548:n
1546:/
1544:m
1540:2
1519:.
1514:n
1510:3
1506:=
1501:m
1497:2
1471:n
1467:3
1463:=
1458:n
1454:)
1448:n
1444:/
1440:m
1436:2
1432:(
1409:3
1406:=
1401:n
1397:/
1393:m
1389:2
1362:.
1357:n
1354:m
1349:=
1346:3
1338:2
1320:n
1316:m
1312:2
1305:2
1301:2
1279:k
1274:k
1218:)
1212:(
1207:)
1203:(
1193:·
1186:·
1179:·
1172:·
1145:.
1099:e
1071:n
1067:n
1063:e
1007:(
948:3
944:5
939:1
935:3
853:"
771:π
663:x
659:x
655:x
651:x
647:x
643:x
598:b
594:c
590:c
586:b
579:b
575:b
568:b
564:b
560:y
556:y
551:.
549:b
545:y
540:.
538:b
534:y
530:b
526:c
522:c
518:y
513:.
511:y
507:c
503:y
499:c
495:y
491:c
484:y
480:c
476:y
472:c
468:c
461:c
457:c
450:c
446:b
442:c
435:b
431:a
427:b
423:b
421:+
419:b
415:b
413:+
411:a
407:c
392:c
388:b
384:a
379:.
377:b
375::
373:c
369:c
365:b
361:a
309:Q
300:\
287:R
265:N
243:Z
221:Q
199:R
137:π
133:π
105:φ
99:e
93:π
55:(
39:2
20:)
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.