177:
22:
1254:
by an adjacency subroutine that always answers in such a way as to leave an odd number of remaining graphs that have a universal vertex. Until all edges are tested, the total number of remaining graphs will be even, so the algorithm will be unable to determine whether the graph it is querying has a universal vertex.
1253:
if no algorithm can test the property guaranteeing fewer queries. Testing the existence of a universal vertex is evasive, on graphs with an even number of vertices. There are an odd number of these graphs that have a universal vertex. A testing algorithm can be forced to query all pairs of vertices
568:, in which one counts the graphs in which one chosen vertex is universal, then corrects for overcounting by subtracting the counts for graphs with two chosen universal vertices, then adding the counts for graphs with three chosen universal vertices, etc. This produces the formula
269:, formed by systems of triangles connected together at a common shared vertex, the universal vertex. The assumption that the graph is finite is important; there exist infinite graphs in which every two vertices have one shared neighbor, but with no universal vertex.
237:
form a subclass of the trivially perfect graphs, so they also contain a universal vertex. They may be defined as the graphs that can be formed by repeated addition of either a universal vertex or an isolated vertex (one with no incident edges).
525:
695:
1142:
228:
by adding an edge connecting every ancestor–descendant pair in the tree. These always contain a universal vertex, the root of the tree. More strongly they may be characterized as the finite graphs in which every connected
1187:
on how many queries (subroutine calls) are needed to test whether a labeled graph has a property, given access to the graph only through a subroutine that can test whether two given vertices are adjacent. In a graph with
527:
This implies that a strong product has a dominating vertex if and only if both of its factors do; in this case the upper bound on its dominating number is one, and in any other case the lower bound is greater than one.
280:
is a subset of another vertex's closed neighborhood. In a graph with a universal vertex, any removal sequence that leaves the universal vertex in place, removing all of the other vertices, fits this definition.
253:
vertex to all the faces of a lower-dimensional base, including all of the vertices of the base. The polytope is said to be pyramidal at its apex, and it may have more than one apex. However, the existence of
1582:
1611:
426:
807:
265:
states that, if every two vertices in a finite graph have exactly one shared neighbor, then the graph contains a universal vertex. The graphs described by this theorem are the
1247:
758:
363:
114:, showing that there are an odd number of such graphs on any even number of vertices. This, in turn, can be used to show that the property of having a universal graph is
1068:
421:
392:
325:
goes to infinity. The dismantlable graphs are also called cop-win graphs, because the side playing the cop wins a certain cop-and-robber game defined on these graphs.
882:
1043:
958:
1016:
840:
166:
573:
1206:
1178:
1063:
986:
926:
902:
717:
558:
323:
303:
140:
332:, a set that includes or is adjacent to every vertex. For this reason, in the context of dominating set problems, a universal vertex may also be called a
118:: testing this property may require checking the adjacency of all pairs of vertices. However, a universal vertex can be recognized immediately from its
1357:
1318:, Graduate Studies in Mathematics, vol. 89, Atlantic Association for Research in the Mathematical Sciences (AARMS), Halifax, NS, p. 7,
1826:; Golovach, Petr A.; Thilikos, Dimitrios M. (2021), "Parameterized complexity of elimination distance to first-order logic properties",
258:
means that the graph of a polytope may have a universal vertex, or all vertices universal, without the polytope itself being a pyramid.
1409:(1977), "Aggregation of inequalities in integer programming", in Hammer, P. L.; Johnson, E. L.; Korte, B. H.; Nemhauser, G. L. (eds.),
1184:
115:
1808:
852:
168:. Universal vertices can be described by a short logical formula, which has been used in graph algorithms for related properties.
809:
is the number of pairs of vertices that do not include a chosen universal vertex, and taking this number as the exponent of a
1853:
1710:
1451:
1331:
1551:
1183:
The property of having a universal vertex (or equivalently an isolated vertex) has been considered with respect to the
565:
1587:
1803:"Sequence A327367 (Number of labeled simple graphs with n vertices, at least one of which is isolated)"
1646:
1644:
Bonato, Anthony; Kemkes, Graeme; Prałat, Paweł (2012), "Almost all cop-win graphs contain a universal vertex",
1615:
1277:
209:
1882:
1828:
36th Annual ACM/IEEE Symposium on Logic in
Computer Science, LICS 2021, Rome, Italy, June 29 - July 2, 2021
277:
249:, and more generally a higher-dimensional pyramid is a polytope whose faces of all dimensions connect an
763:
103:, the vertex at the apex of the pyramid is universal. When a graph contains a universal vertex, it is a
1149:
1211:
722:
1153:
1157:
1145:
337:
342:
64:
of the cone. This terminology should be distinguished from the unrelated usage of these words for
520:{\displaystyle \max\{\gamma (G),\gamma (H)\}\leq \gamma (G\boxtimes H)\leq \gamma (G)\gamma (H).}
221:
111:
84:
397:
368:
1272:
1733:
Fisher, David C. (1994), "Domination, fractional domination, 2-packing, and graph products",
1690:
1433:
1406:
989:
119:
41:
1772:
1313:
861:
1754:
1720:
1669:
1490:
1388:
1341:
1298:
1028:
1021:
The property of having a universal vertex can be expressed by a formula in the first-order
931:
690:{\displaystyle \displaystyle \sum _{k=1}^{n}(-1)^{k+1}{\binom {n}{k}}2^{\tbinom {n-k}{2}}.}
65:
276:, meaning that it can be reduced to a single vertex by repeatedly removing a vertex whose
8:
1541:
1413:, Annals of Discrete Mathematics, vol. 1, Amsterdam: North-Holland, pp. 145–162
1402:
995:
819:
255:
205:
201:
181:
145:
80:
328:
When a graph has a universal vertex, the vertex set consisting only of that vertex is a
208:
that have a universal vertex, and may be constructed by adding a universal vertex to an
1859:
1831:
1776:
1429:
1376:
1191:
1163:
1048:
971:
911:
887:
702:
543:
308:
288:
273:
242:
125:
305:-vertex dismantlable graphs that have a universal vertex tends to one in the limit as
1863:
1849:
1706:
1507:
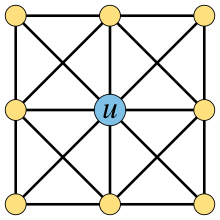
1447:
1327:
905:
1425:
1845:
1841:
1742:
1698:
1686:
1655:
1624:
1478:
1439:
1366:
1319:
1286:
1137:{\displaystyle \exists u\forall v{\bigl (}(u\neq v)\Rightarrow (u\sim v){\bigr )}.}
561:
266:
230:
189:
88:
45:
845:
1, 1, 4, 23, 256, 5319, 209868, 15912975, 2343052576, 675360194287, ... (sequence
1750:
1716:
1665:
1486:
1384:
1337:
1294:
1022:
250:
234:
196:(lower right). In each example the universal vertex is the center yellow vertex.
193:
176:
69:
1660:
1290:
560:
vertices, at least one of which is universal (or equivalently isolated, in the
329:
285:
dismantlable graphs have a universal vertex, in the sense that the fraction of
53:
1746:
1702:
1511:
1443:
928:-vertex unlabeled graphs with a universal vertex is the same as the number of
1876:
1775:; Young, Neal E. (2002), "Lecture Notes on Evasiveness of Graph Properties",
1275:; Pizaña, M. A. (2004), "The clique operator on cographs and serial graphs",
537:
110:
The number of labeled graphs containing a universal vertex can be counted by
104:
48:
that is adjacent to all other vertices of the graph. It may also be called a
1503:
1144:
The existence of this formula, and its small number of alternations between
1629:
1545:
1515:
1482:
1208:
vertices, one can determine the entire graph, and test any property, using
810:
33:
1823:
1798:
1466:
225:
217:
213:
185:
92:
1380:
282:
246:
73:
56:
in the graph. A graph that contains a universal vertex may be called a
1323:
1371:
1836:
1781:
813:
counts the number of graphs with the chosen vertices as universal.
100:
21:
1270:
1697:, Springer Monographs in Mathematics, Springer, Cham, p. 2,
96:
1540:
1065:
has a universal vertex if and only if it models the formula
107:, and almost all cop-win graphs contain a universal vertex.
1802:
847:
1469:(1964), "On the number of vertices of a convex polytope",
1355:
Wolk, E. S. (1962), "The comparability graph of a tree",
1411:
Studies in
Integer Programming (Proc. Worksh. Bonn 1975)
1685:
1548:; Rosenberg, Ivo G.; Davies, Roy O. (1976), "There are
1045:
to indicate the adjacency relation in a graph, a graph
904:
is even, and vice versa. The unlabeled version of this
1797:
1591:
1555:
1216:
768:
727:
719:
is the number of vertices chosen to be universal, and
651:
1822:
1590:
1554:
1214:
1194:
1166:
1160:
of a graph can be made to have universal vertices by
1071:
1051:
1031:
998:
974:
934:
914:
890:
864:
822:
766:
725:
705:
577:
576:
546:
429:
400:
371:
345:
311:
291:
148:
128:
908:
problem is trivial, in the sense that the number of
79:Graphs that contain a universal vertex include the
1643:
1605:
1577:{\displaystyle \scriptstyle 2^{\aleph _{\alpha }}}
1576:
1241:
1200:
1172:
1136:
1057:
1037:
1010:
980:
952:
920:
896:
876:
834:
801:
752:
711:
689:
552:
519:
415:
386:
357:
317:
297:
160:
134:
1424:
640:
627:
1874:
1358:Proceedings of the American Mathematical Society
1180:steps of removing a vertex from each component.
430:
272:Every finite graph with a universal vertex is a
216:may be formed by adding a universal vertex to a
171:
988:vertices, a universal vertex is a vertex whose
180:Four types of graph with a universal vertex: a
1767:
1765:
1763:
1606:{\displaystyle \scriptstyle \aleph _{\alpha }}
99:), and graphs of higher-dimensional pyramidal
1502:
1401:
1232:
1219:
1126:
1086:
792:
771:
743:
730:
675:
654:
60:, and its universal vertex may be called the
531:
463:
433:
1771:
1760:
1271:Larrión, F.; de Mello, C. P.; Morgana, A.;
760:is the number of ways to make this choice.
233:contains a universal vertex. The connected
1835:
1809:On-Line Encyclopedia of Integer Sequences
1780:
1659:
1628:
1370:
1435:Configuration from a Graphical Viewpoint
175:
20:
16:Vertex adjacent to all others in a graph
1793:
1791:
1875:
1732:
1311:
1681:
1679:
1788:
1735:SIAM Journal on Discrete Mathematics
1465:
1354:
1695:Domination in Graphs: Core Concepts
241:In geometry, the three-dimensional
13:
1676:
1593:
1562:
1223:
1185:Aanderaa–Karp–Rosenberg conjecture
1156:algorithm for testing whether all
1078:
1072:
802:{\displaystyle {\tbinom {n-k}{2}}}
775:
734:
658:
631:
14:
1894:
25:A graph with a universal vertex,
1242:{\displaystyle {\tbinom {n}{2}}}
753:{\displaystyle {\tbinom {n}{k}}}
1816:
1726:
1471:Canadian Journal of Mathematics
842:, these numbers of graphs are:
1846:10.1109/LICS52264.2021.9470540
1693:; Henning, Michael A. (2023),
1637:
1616:Canadian Mathematical Bulletin
1584:friendship graphs of cardinal
1534:
1516:"On a problem of graph theory"
1496:
1459:
1418:
1395:
1348:
1305:
1264:
1121:
1109:
1106:
1103:
1091:
963:
947:
935:
609:
599:
511:
505:
499:
493:
484:
472:
460:
454:
445:
439:
410:
404:
381:
375:
1:
1257:
1249:queries. A graph property is
884:, these numbers are odd when
566:inclusion–exclusion principle
172:In special families of graphs
142:-vertex graph, it has degree
358:{\displaystyle G\boxtimes H}
52:, as it forms a one-element
7:
245:have wheel graphs as their
10:
1899:
1799:Sloane, N. J. A.
1661:10.1016/j.disc.2012.02.018
1291:10.1016/j.disc.2003.10.023
416:{\displaystyle \gamma (H)}
387:{\displaystyle \gamma (G)}
1747:10.1137/S0895480191217806
1703:10.1007/978-3-031-09496-5
1523:Studia Sci. Math. Hungar.
1444:10.1007/978-0-8176-8364-1
1315:A course on the web graph
1154:fixed-parameter tractable
699:In each term of the sum,
532:Combinatorial enumeration
365:, the domination numbers
1438:, Springer, p. 21,
1312:Bonato, Anthony (2008),
564:) can be counted by the
338:strong product of graphs
222:trivially perfect graphs
85:trivially perfect graphs
1830:, IEEE, pp. 1–13,
1691:Hedetniemi, Stephen T.
1630:10.4153/cmb-1976-064-1
1607:
1578:
1483:10.4153/CJM-1964-067-6
1407:Hammer, Peter Ladislaw
1243:
1202:
1174:
1150:existential quantifers
1138:
1059:
1039:
1012:
982:
954:
922:
898:
878:
877:{\displaystyle n>1}
836:
803:
754:
713:
691:
598:
554:
521:
423:obey the inequalities
417:
388:
359:
319:
299:
197:
162:
136:
29:
1608:
1579:
1244:
1203:
1175:
1139:
1060:
1040:
1038:{\displaystyle \sim }
1013:
983:
955:
953:{\displaystyle (n-1)}
923:
899:
879:
837:
804:
755:
714:
692:
578:
555:
522:
418:
389:
360:
320:
300:
179:
163:
137:
66:universal quantifiers
24:
1883:Graph theory objects
1647:Discrete Mathematics
1588:
1552:
1278:Discrete Mathematics
1212:
1192:
1164:
1069:
1049:
1029:
996:
972:
932:
912:
888:
862:
820:
764:
723:
703:
574:
544:
427:
398:
369:
343:
309:
289:
256:neighborly polytopes
146:
126:
1430:Servatius, Brigitte
1152:, can be used in a
1011:{\displaystyle n-1}
835:{\displaystyle n=1}
278:closed neighborhood
161:{\displaystyle n-1}
112:inclusion–exclusion
1603:
1602:
1574:
1573:
1239:
1237:
1198:
1170:
1134:
1055:
1035:
1008:
978:
950:
918:
894:
874:
832:
799:
797:
750:
748:
709:
687:
686:
680:
550:
517:
413:
384:
355:
315:
295:
274:dismantlable graph
263:friendship theorem
224:are obtained from
198:
192:(lower left), and
158:
132:
30:
1855:978-1-6654-4895-6
1812:, OEIS Foundation
1712:978-3-031-09495-8
1687:Haynes, Teresa W.
1654:(10): 1652–1657,
1453:978-0-8176-8363-4
1333:978-0-8218-4467-0
1230:
1201:{\displaystyle n}
1173:{\displaystyle k}
1058:{\displaystyle G}
981:{\displaystyle n}
921:{\displaystyle n}
906:graph enumeration
897:{\displaystyle n}
790:
741:
712:{\displaystyle k}
673:
638:
553:{\displaystyle n}
334:dominating vertex
318:{\displaystyle n}
298:{\displaystyle n}
267:friendship graphs
135:{\displaystyle n}
89:friendship graphs
50:dominating vertex
1890:
1867:
1866:
1839:
1820:
1814:
1813:
1795:
1786:
1785:
1784:
1769:
1758:
1757:
1730:
1724:
1723:
1683:
1674:
1672:
1663:
1641:
1635:
1633:
1632:
1612:
1610:
1609:
1604:
1601:
1600:
1583:
1581:
1580:
1575:
1572:
1571:
1570:
1569:
1538:
1532:
1530:
1520:
1500:
1494:
1493:
1463:
1457:
1456:
1422:
1416:
1414:
1399:
1393:
1391:
1374:
1352:
1346:
1344:
1309:
1303:
1301:
1285:(1–3): 183–191,
1273:Neumann-Lara, V.
1268:
1248:
1246:
1245:
1240:
1238:
1236:
1235:
1222:
1207:
1205:
1204:
1199:
1179:
1177:
1176:
1171:
1143:
1141:
1140:
1135:
1130:
1129:
1090:
1089:
1064:
1062:
1061:
1056:
1044:
1042:
1041:
1036:
1017:
1015:
1014:
1009:
987:
985:
984:
979:
968:In a graph with
960:-vertex graphs.
959:
957:
956:
951:
927:
925:
924:
919:
903:
901:
900:
895:
883:
881:
880:
875:
850:
841:
839:
838:
833:
808:
806:
805:
800:
798:
796:
795:
786:
774:
759:
757:
756:
751:
749:
747:
746:
733:
718:
716:
715:
710:
696:
694:
693:
688:
682:
681:
679:
678:
669:
657:
645:
644:
643:
630:
623:
622:
597:
592:
562:complement graph
559:
557:
556:
551:
526:
524:
523:
518:
422:
420:
419:
414:
393:
391:
390:
385:
364:
362:
361:
356:
324:
322:
321:
316:
304:
302:
301:
296:
235:threshold graphs
231:induced subgraph
204:are exactly the
190:friendship graph
167:
165:
164:
159:
141:
139:
138:
133:
46:undirected graph
38:universal vertex
28:
1898:
1897:
1893:
1892:
1891:
1889:
1888:
1887:
1873:
1872:
1871:
1870:
1856:
1824:Fomin, Fedor V.
1821:
1817:
1796:
1789:
1770:
1761:
1731:
1727:
1713:
1684:
1677:
1642:
1638:
1596:
1592:
1589:
1586:
1585:
1565:
1561:
1560:
1556:
1553:
1550:
1549:
1542:Chvátal, Václav
1539:
1535:
1518:
1501:
1497:
1464:
1460:
1454:
1426:Pisanski, Tomaž
1423:
1419:
1403:Chvátal, Václav
1400:
1396:
1372:10.2307/2034179
1353:
1349:
1334:
1324:10.1090/gsm/089
1310:
1306:
1269:
1265:
1260:
1231:
1218:
1217:
1215:
1213:
1210:
1209:
1193:
1190:
1189:
1165:
1162:
1161:
1125:
1124:
1085:
1084:
1070:
1067:
1066:
1050:
1047:
1046:
1030:
1027:
1026:
1023:logic of graphs
997:
994:
993:
973:
970:
969:
966:
933:
930:
929:
913:
910:
909:
889:
886:
885:
863:
860:
859:
856:
846:
821:
818:
817:
791:
776:
770:
769:
767:
765:
762:
761:
742:
729:
728:
726:
724:
721:
720:
704:
701:
700:
697:
674:
659:
653:
652:
650:
646:
639:
626:
625:
624:
612:
608:
593:
582:
575:
572:
571:
545:
542:
541:
534:
428:
425:
424:
399:
396:
395:
370:
367:
366:
344:
341:
340:
310:
307:
306:
290:
287:
286:
210:independent set
194:threshold graph
188:(upper right),
174:
147:
144:
143:
127:
124:
123:
95:(the graphs of
70:logic of graphs
26:
17:
12:
11:
5:
1896:
1886:
1885:
1869:
1868:
1854:
1815:
1787:
1773:Lovász, László
1759:
1741:(3): 493–498,
1725:
1711:
1675:
1636:
1623:(4): 431–433,
1599:
1595:
1568:
1564:
1559:
1533:
1495:
1458:
1452:
1417:
1394:
1365:(5): 789–795,
1347:
1332:
1304:
1262:
1261:
1259:
1256:
1234:
1229:
1226:
1221:
1197:
1169:
1133:
1128:
1123:
1120:
1117:
1114:
1111:
1108:
1105:
1102:
1099:
1096:
1093:
1088:
1083:
1080:
1077:
1074:
1054:
1034:
1007:
1004:
1001:
977:
965:
962:
949:
946:
943:
940:
937:
917:
893:
873:
870:
867:
844:
831:
828:
825:
816:Starting from
794:
789:
785:
782:
779:
773:
745:
740:
737:
732:
708:
685:
677:
672:
668:
665:
662:
656:
649:
642:
637:
634:
629:
621:
618:
615:
611:
607:
604:
601:
596:
591:
588:
585:
581:
570:
549:
538:labeled graphs
536:The number of
533:
530:
516:
513:
510:
507:
504:
501:
498:
495:
492:
489:
486:
483:
480:
477:
474:
471:
468:
465:
462:
459:
456:
453:
450:
447:
444:
441:
438:
435:
432:
412:
409:
406:
403:
383:
380:
377:
374:
354:
351:
348:
330:dominating set
314:
294:
184:(upper left),
173:
170:
157:
154:
151:
131:
54:dominating set
15:
9:
6:
4:
3:
2:
1895:
1884:
1881:
1880:
1878:
1865:
1861:
1857:
1851:
1847:
1843:
1838:
1833:
1829:
1825:
1819:
1811:
1810:
1804:
1800:
1794:
1792:
1783:
1778:
1774:
1768:
1766:
1764:
1756:
1752:
1748:
1744:
1740:
1736:
1729:
1722:
1718:
1714:
1708:
1704:
1700:
1696:
1692:
1688:
1682:
1680:
1671:
1667:
1662:
1657:
1653:
1649:
1648:
1640:
1631:
1626:
1622:
1618:
1617:
1597:
1566:
1557:
1547:
1546:Kotzig, Anton
1543:
1537:
1528:
1524:
1517:
1513:
1509:
1508:Rényi, Alfréd
1505:
1499:
1492:
1488:
1484:
1480:
1476:
1472:
1468:
1462:
1455:
1449:
1445:
1441:
1437:
1436:
1431:
1427:
1421:
1412:
1408:
1404:
1398:
1390:
1386:
1382:
1378:
1373:
1368:
1364:
1360:
1359:
1351:
1343:
1339:
1335:
1329:
1325:
1321:
1317:
1316:
1308:
1300:
1296:
1292:
1288:
1284:
1280:
1279:
1274:
1267:
1263:
1255:
1252:
1227:
1224:
1195:
1186:
1181:
1167:
1159:
1155:
1151:
1147:
1131:
1118:
1115:
1112:
1100:
1097:
1094:
1081:
1075:
1052:
1032:
1024:
1019:
1005:
1002:
999:
991:
975:
961:
944:
941:
938:
915:
907:
891:
871:
868:
865:
854:
849:
843:
829:
826:
823:
814:
812:
787:
783:
780:
777:
738:
735:
706:
683:
670:
666:
663:
660:
647:
635:
632:
619:
616:
613:
605:
602:
594:
589:
586:
583:
579:
569:
567:
563:
547:
539:
529:
514:
508:
502:
496:
490:
487:
481:
478:
475:
469:
466:
457:
451:
448:
442:
436:
407:
401:
378:
372:
352:
349:
346:
339:
335:
331:
326:
312:
292:
284:
279:
275:
270:
268:
264:
259:
257:
252:
248:
244:
239:
236:
232:
227:
223:
219:
215:
211:
207:
203:
195:
191:
187:
183:
178:
169:
155:
152:
149:
129:
121:
117:
113:
108:
106:
105:cop-win graph
102:
98:
94:
90:
86:
82:
77:
75:
71:
67:
63:
59:
55:
51:
47:
43:
39:
35:
23:
19:
1827:
1818:
1806:
1738:
1734:
1728:
1694:
1651:
1645:
1639:
1620:
1614:
1536:
1526:
1522:
1512:Sós, Vera T.
1498:
1474:
1470:
1467:Klee, Victor
1461:
1434:
1420:
1410:
1397:
1362:
1356:
1350:
1314:
1307:
1282:
1276:
1266:
1250:
1182:
1020:
967:
857:
815:
811:power of two
698:
535:
333:
327:
271:
262:
260:
240:
226:rooted trees
214:wheel graphs
199:
109:
93:wheel graphs
78:
61:
57:
49:
37:
34:graph theory
31:
18:
1504:Erdős, Paul
1477:: 701–720,
992:is exactly
964:Recognition
218:cycle graph
186:wheel graph
74:apex graphs
1837:2104.02998
1782:cs/0205031
1258:References
1158:components
336:. For the
283:Almost all
72:, and for
1864:233169117
1598:α
1594:ℵ
1567:α
1563:ℵ
1529:: 215–235
1146:universal
1116:∼
1107:⇒
1098:≠
1079:∀
1073:∃
1033:∼
1003:−
942:−
781:−
664:−
603:−
580:∑
503:γ
491:γ
488:≤
479:⊠
470:γ
467:≤
452:γ
437:γ
402:γ
373:γ
350:⊠
247:skeletons
153:−
101:polytopes
1877:Category
1514:(1966),
1432:(2013),
1025:. Using
243:pyramids
122:: in an
97:pyramids
1801:(ed.),
1755:1285586
1721:4607811
1670:2901161
1491:0166682
1389:0172273
1381:2034179
1342:2389013
1299:2059518
1251:evasive
851:in the
848:A327367
212:. The
116:evasive
68:in the
1862:
1852:
1753:
1719:
1709:
1668:
1489:
1450:
1387:
1379:
1340:
1330:
1297:
990:degree
220:. The
120:degree
91:. For
87:, and
44:of an
42:vertex
1860:S2CID
1832:arXiv
1777:arXiv
1519:(PDF)
1377:JSTOR
540:with
206:trees
202:stars
81:stars
40:is a
1850:ISBN
1807:The
1707:ISBN
1448:ISBN
1328:ISBN
1148:and
869:>
858:For
853:OEIS
394:and
261:The
251:apex
200:The
182:star
62:apex
58:cone
36:, a
1842:doi
1743:doi
1699:doi
1656:doi
1652:312
1625:doi
1613:",
1479:doi
1440:doi
1367:doi
1320:doi
1287:doi
1283:282
431:max
32:In
1879::
1858:,
1848:,
1840:,
1805:,
1790:^
1762:^
1751:MR
1749:,
1737:,
1717:MR
1715:,
1705:,
1689:;
1678:^
1666:MR
1664:,
1650:,
1621:19
1619:,
1544:;
1525:,
1521:,
1510:;
1506:;
1487:MR
1485:,
1475:16
1473:,
1446:,
1428:;
1405:;
1385:MR
1383:,
1375:,
1363:13
1361:,
1338:MR
1336:,
1326:,
1295:MR
1293:,
1281:,
1018:.
855:).
83:,
76:.
1844::
1834::
1779::
1745::
1739:7
1701::
1673:.
1658::
1634:.
1627::
1558:2
1531:.
1527:1
1481::
1442::
1415:.
1392:.
1369::
1345:.
1322::
1302:.
1289::
1233:)
1228:2
1225:n
1220:(
1196:n
1168:k
1132:.
1127:)
1122:)
1119:v
1113:u
1110:(
1104:)
1101:v
1095:u
1092:(
1087:(
1082:v
1076:u
1053:G
1006:1
1000:n
976:n
948:)
945:1
939:n
936:(
916:n
892:n
872:1
866:n
830:1
827:=
824:n
793:)
788:2
784:k
778:n
772:(
744:)
739:k
736:n
731:(
707:k
684:.
676:)
671:2
667:k
661:n
655:(
648:2
641:)
636:k
633:n
628:(
620:1
617:+
614:k
610:)
606:1
600:(
595:n
590:1
587:=
584:k
548:n
515:.
512:)
509:H
506:(
500:)
497:G
494:(
485:)
482:H
476:G
473:(
464:}
461:)
458:H
455:(
449:,
446:)
443:G
440:(
434:{
411:)
408:H
405:(
382:)
379:G
376:(
353:H
347:G
313:n
293:n
156:1
150:n
130:n
27:u
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.