180:
166:
226:
457:
450:
443:
464:
436:
429:
422:
313:
415:
728:
320:
717:
739:
20:
773:
751:
A polyhedron that is formed by a system of crossing polygons corresponds to an abstract topological manifold formed by its polygons and their system of shared edges and vertices, and the genus of the polyhedron may be determined from this abstract manifold. Examples include the genus-1
94:
as they do. That is, each edge should be shared by exactly two polygons, and at each vertex the edges and faces that meet at the vertex should be linked together in a single cycle of alternating edges and faces, the
217:
The Császár polyhedron has the fewest possible vertices of any embedded toroidal polyhedron, and the
Szilassi polyhedron has the fewest possible faces of any embedded toroidal polyhedron.
288:. For such a polyhedron, each face of the convex hull either lies on the surface of the toroid, or is a polygon all of whose edges lie on the surface of the toroid.
1150:; see messages dated "Sep 23, 1997, 12:00:00 AM" announcing the toroidal deltahedron, and "Sep 25, 1997, 12:00:00 AM" describing its construction. Unlike the
122:, topological surfaces without any specified geometric realization. Intermediate between these two extremes are polyhedra formed by geometric polygons or
257:
faces, without crossings, and with a further restriction that adjacent faces may not lie in the same plane as each other. These are called
103:. Some authors restrict the phrase "toroidal polyhedra" to mean more specifically polyhedra topologically equivalent to the (genus 1)
206:
are the only known polyhedra in which every possible line segment connecting two vertices forms an edge of the polyhedron. Its dual, the
1310:
1305:
1210:
1061:
1138:
1031:
1261:, NATO ASI Series C: Mathematical and Physical Series, vol. 440, Kluwer Academic Publishers, pp. 43–70,
1154:, it has coplanar adjacent triangles, but otherwise resembles a toroidal deltahedron with more faces described by
273:; however, unlike the Johnson solids, there are infinitely many Stewart toroids. They include also toroidal
1200:
210:, has seven hexagonal faces that are all adjacent to each other, hence providing the existence half of the
129:
In all of these cases the toroidal nature of a polyhedron can be verified by its orientability and by its
1335:
921:
184:
211:
170:
179:
757:
732:
612:
607:
602:
597:
199:
195:
Two of the simplest possible embedded toroidal polyhedra are the Császár and
Szilassi polyhedra.
165:
71:
592:
60:
1271:
1254:
821:
245:. Conway suggested that it should be the deltahedral toroid with the fewest possible faces.
1185:
936:
895:
832:
809:
587:
582:
130:
1027:
1004:
8:
874:
207:
75:
63:
1291:
202:
is a seven-vertex toroidal polyhedron with 21 edges and 14 triangular faces. It and the
1169:
1115:
1067:
1039:
899:
761:
753:
743:
721:
119:
1250:
965:
1315:
1288:
1206:
1057:
987:
903:
826:
777:
567:
540:
529:
497:
486:
456:
449:
442:
270:
1071:
463:
214:
that the maximum number of colors needed for a map on a (genus one) torus is seven.
1262:
1097:
1049:
977:
883:
805:
797:
781:
508:
435:
28:
968:; Szilassi, Lajos (2009), "Geometric Realizations of Special Toroidal Complexes",
428:
421:
1181:
1053:
932:
917:
891:
801:
331:
254:
115:
96:
1266:
1202:
Adventures Among the
Toroids: A Study of Orientable Polyhedra with Regular Faces
1085:
872:
Webber, William T. (1997), "Monohedral idemvalent polyhedra that are toroids",
837:
577:
513:
502:
491:
262:
238:
1320:
1030:(2008), "Polyhedral Surfaces of High Genus", in Bobenko, A. I.; Schröder, P.;
887:
225:
1329:
991:
562:
551:
524:
475:
312:
266:
100:
982:
414:
123:
727:
1038:, Oberwolfach Seminars, vol. 38, Springer-Verlag, pp. 191–213,
319:
285:
274:
234:
203:
1044:
280:
A restricted class of
Stewart toroids, also defined by Stewart, are the
253:
A special category of toroidal polyhedra are constructed exclusively by
950:
808:(equal faces). Crown polyhedra are self-intersecting and topologically
518:
480:
114:
toroidal polyhedra, whose faces are flat polygons in three-dimensional
44:
241:
in 1997, containing 18 vertices and 36 faces. Some adjacent faces are
1296:
1101:
738:
716:
337:
111:
284:. These are Stewart toroids that include all of the edges of their
242:
91:
36:
19:
87:
1144:
48:
772:
104:
56:
24:
1306:
Stewart
Toroids (Toroidal Solids with Regular Polygon Faces)
1286:
133:
being non-positive. The Euler characteristic generalizes to
556:
545:
534:
99:
of the vertex. For toroidal polyhedra, this manifold is an
265:, who studied them intensively. They are analogous to the
27:
can be constructed to approximate a torus surface, from a
126:
in
Euclidean space that are allowed to cross each other.
1240:, "Quasi-convexity and weak quasi-convexity", pp. 76–79.
292:
Stewart toroids by augmentation of a single polyhedron
277:, polyhedra whose faces are all equilateral triangles.
776:
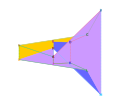
Pentagonal stephanoid. This stephanoid has pentagonal
183:Interactive Szilassi polyhedron model – in
156:
118:that do not cross themselves or each other, from
90:that meet at their edges and vertices, forming a
86:Toroidal polyhedra are defined as collections of
1327:
964:
220:
169:Interactive Csaszar polyhedron model – in
70:) of 1 or greater. Notable examples include the
1114:
955:, Bolyai Institute, University of Szeged, 1949
31:of quadrilateral faces, like this 6x4 example.
1259:Polytopes: Abstract, Convex and Computational
110:In this area, it is important to distinguish
16:Partition of a toroidal surface into polygons
1003:
173:move the mouse left and right to rotate it.
81:
1007:(1949), "A polyhedron without diagonals",
707:
1043:
981:
780:and has the same vertices as the uniform
1249:
1084:
916:
855:
771:
224:
178:
164:
18:
1237:
1225:
1198:
1155:
1026:
859:
796:is a toroidal polyhedron which is also
1328:
871:
1287:
970:Contributions to Discrete Mathematics
1167:
1151:
13:
1136:
1118:(1890), "Map colouring theorems",
767:
248:
14:
1347:
1280:
1120:Quarterly Journal of Mathematics
737:
726:
715:
462:
455:
448:
441:
434:
427:
420:
413:
318:
311:
1243:
1231:
1219:
1205:(2nd ed.), B. M. Stewart,
1192:
1161:
1130:
952:A Polyhedron Without Diagonals.
282:quasi-convex toroidal polyhedra
1170:"Stella: polyhedron navigator"
1108:
1078:
1036:Discrete Differential Geometry
1020:
997:
958:
943:
910:
865:
849:
711:
160:
157:Császár and Szilassi polyhedra
1:
1255:"Polyhedra with Hollow Faces"
1174:Symmetry: Culture and Science
1139:"Polyhedra of positive genus"
843:
379:Quasi-convex Stewart toroids
229:Conway's toroidal deltahedron
221:Conway's toroidal deltahedron
1054:10.1007/978-3-7643-8621-4_10
922:"Realizability of polyhedra"
713:
675:
646:
617:
469:
364:
353:
342:
325:
187:move the mouse to rotate it.
7:
1267:10.1007/978-94-011-0924-6_3
1088:(1986), "Regular toroids",
815:
10:
1352:
829:(infinite skew polyhedron)
177:
163:
153:is its topological genus.
1034:; Ziegler, G. M. (eds.),
386:
82:Variations in definition
1199:Stewart, B. M. (1980),
983:10.11575/cdm.v4i1.61986
888:10.1023/A:1004997029852
758:small cubicuboctahedron
733:Small cubicuboctahedron
708:Self-crossing polyhedra
613:truncated cuboctahedron
608:truncated cuboctahedron
603:truncated cuboctahedron
598:truncated cuboctahedron
1152:§ Stewart toroids
1009:Acta Sci. Math. Szeged
785:
593:expanded cuboctahedron
230:
188:
174:
32:
1292:"Toroidal polyhedron"
1168:Webb, Robert (2000),
822:Projective polyhedron
804:(equal vertices) and
775:
228:
182:
168:
22:
1270:. See in particular
833:Spherical polyhedron
588:truncated octahedron
583:truncated octahedron
131:Euler characteristic
1311:Stewart's polyhedra
1090:Structural Topology
929:Structural Topology
875:Geometriae Dedicata
380:
293:
208:Szilassi polyhedron
41:toroidal polyhedron
1336:Toroidal polyhedra
1316:Toroidal Polyhedra
1289:Weisstein, Eric W.
1143:geometry.research
1028:Ziegler, Günter M.
786:
762:great dodecahedron
760:, and the genus-4
754:octahemioctahedron
744:Great dodecahedron
722:Octahemioctahedron
568:triangular cupolae
541:triangular cupolae
530:triangular cupolae
498:triangular cupolae
487:triangular cupolae
378:
291:
231:
200:Császár polyhedron
189:
175:
120:abstract polyhedra
101:orientable surface
76:Szilassi polyhedra
33:
1212:978-0-686-11936-4
1063:978-3-7643-8620-7
827:Skew apeirohedron
778:dihedral symmetry
749:
748:
705:
704:
509:triangular prisms
376:
375:
237:was described by
193:
192:
1343:
1302:
1301:
1275:
1269:
1251:Grünbaum, Branko
1247:
1241:
1235:
1229:
1223:
1217:
1215:
1196:
1190:
1188:
1180:(1–4): 231–268,
1165:
1159:
1149:
1134:
1128:
1127:
1122:, First Series,
1112:
1106:
1104:
1082:
1076:
1074:
1047:
1024:
1018:
1016:
1001:
995:
994:
985:
966:Grünbaum, Branko
962:
956:
947:
941:
939:
931:(1): 46–58, 73,
926:
918:Whiteley, Walter
914:
908:
906:
869:
863:
853:
790:crown polyhedron
782:pentagonal prism
741:
730:
719:
712:
466:
459:
452:
445:
438:
431:
424:
417:
381:
377:
332:hexagonal prisms
322:
315:
294:
290:
271:convex polyhedra
161:
69:
54:
47:which is also a
1351:
1350:
1346:
1345:
1344:
1342:
1341:
1340:
1326:
1325:
1321:Stewart toroids
1283:
1278:
1248:
1244:
1236:
1232:
1224:
1220:
1213:
1197:
1193:
1166:
1162:
1135:
1131:
1113:
1109:
1086:Szilassi, Lajos
1083:
1079:
1064:
1045:math.MG/0412093
1032:Sullivan, J. M.
1025:
1021:
1002:
998:
963:
959:
948:
944:
924:
915:
911:
870:
866:
856:Whiteley (1979)
854:
850:
846:
818:
770:
768:Crown polyhedra
742:
731:
720:
710:
565:
554:
543:
532:
527:
516:
514:square pyramids
511:
503:square pyramids
500:
492:square pyramids
489:
478:
269:in the case of
259:Stewart toroids
255:regular polygon
251:
249:Stewart toroids
223:
159:
116:Euclidean space
84:
67:
52:
17:
12:
11:
5:
1349:
1339:
1338:
1324:
1323:
1318:
1313:
1308:
1303:
1282:
1281:External links
1279:
1277:
1276:
1242:
1238:Stewart (1980)
1230:
1226:Stewart (1980)
1218:
1211:
1191:
1160:
1156:Stewart (1980)
1137:Conway, John,
1129:
1116:Heawood, P. J.
1107:
1077:
1062:
1019:
996:
957:
949:Ákos Császár,
942:
909:
864:
860:Stewart (1980)
847:
845:
842:
841:
840:
838:Toroidal graph
835:
830:
824:
817:
814:
769:
766:
756:, the genus-3
747:
746:
735:
724:
709:
706:
703:
702:
699:
696:
693:
690:
687:
684:
681:
678:
674:
673:
670:
667:
664:
661:
658:
655:
652:
649:
645:
644:
641:
638:
635:
632:
629:
626:
623:
620:
616:
615:
610:
605:
600:
595:
590:
585:
580:
578:truncated cube
575:
571:
570:
563:square cupolae
559:
552:square cupolae
548:
537:
525:square cupolae
521:
505:
494:
483:
476:square cupolae
472:
468:
467:
460:
453:
446:
439:
432:
425:
418:
411:
407:
406:
403:
400:
397:
394:
391:
388:
385:
374:
373:
370:
367:
363:
362:
359:
356:
352:
351:
348:
345:
341:
340:
334:
328:
324:
323:
316:
309:
305:
304:
301:
298:
267:Johnson solids
263:Bonnie Stewart
261:, named after
250:
247:
239:John H. Conway
222:
219:
191:
190:
185:the SVG image,
176:
171:the SVG image,
158:
155:
83:
80:
15:
9:
6:
4:
3:
2:
1348:
1337:
1334:
1333:
1331:
1322:
1319:
1317:
1314:
1312:
1309:
1307:
1304:
1299:
1298:
1293:
1290:
1285:
1284:
1273:
1268:
1264:
1260:
1256:
1252:
1246:
1239:
1234:
1228:, p. 15.
1227:
1222:
1214:
1208:
1204:
1203:
1195:
1187:
1183:
1179:
1175:
1171:
1164:
1157:
1153:
1148:
1146:
1140:
1133:
1125:
1121:
1117:
1111:
1103:
1099:
1095:
1091:
1087:
1081:
1073:
1069:
1065:
1059:
1055:
1051:
1046:
1041:
1037:
1033:
1029:
1023:
1014:
1010:
1006:
1000:
993:
989:
984:
979:
975:
971:
967:
961:
954:
953:
946:
938:
934:
930:
923:
919:
913:
905:
901:
897:
893:
889:
885:
881:
877:
876:
868:
862:, p. 15.
861:
857:
852:
848:
839:
836:
834:
831:
828:
825:
823:
820:
819:
813:
811:
807:
803:
800:, being both
799:
795:
791:
783:
779:
774:
765:
763:
759:
755:
745:
740:
736:
734:
729:
725:
723:
718:
714:
700:
697:
694:
691:
688:
685:
682:
679:
676:
671:
668:
665:
662:
659:
656:
653:
650:
647:
642:
639:
636:
633:
630:
627:
624:
621:
618:
614:
611:
609:
606:
604:
601:
599:
596:
594:
591:
589:
586:
584:
581:
579:
576:
573:
572:
569:
564:
560:
558:
553:
549:
547:
542:
538:
536:
531:
526:
522:
520:
515:
510:
506:
504:
499:
495:
493:
488:
484:
482:
477:
473:
470:
465:
461:
458:
454:
451:
447:
444:
440:
437:
433:
430:
426:
423:
419:
416:
412:
409:
408:
404:
401:
398:
395:
392:
389:
383:
382:
371:
368:
365:
360:
357:
354:
349:
346:
343:
339:
335:
333:
329:
326:
321:
317:
314:
310:
307:
306:
302:
299:
296:
295:
289:
287:
283:
278:
276:
272:
268:
264:
260:
256:
246:
244:
240:
236:
227:
218:
215:
213:
209:
205:
201:
196:
186:
181:
172:
167:
162:
154:
152:
148:
144:
140:
136:
132:
127:
125:
124:star polygons
121:
117:
113:
108:
106:
102:
98:
93:
89:
79:
77:
73:
65:
62:
58:
50:
46:
42:
38:
30:
26:
23:A polyhedral
21:
1295:
1258:
1245:
1233:
1221:
1201:
1194:
1177:
1173:
1163:
1142:
1132:
1123:
1119:
1110:
1093:
1089:
1080:
1035:
1022:
1012:
1008:
999:
976:(1): 21–39,
973:
969:
960:
951:
945:
928:
912:
882:(1): 31–44,
879:
873:
867:
851:
793:
789:
787:
750:
574:Convex hull
286:convex hulls
281:
279:
258:
252:
232:
216:
197:
194:
150:
146:
142:
138:
134:
128:
109:
85:
59:), having a
40:
34:
1005:Császár, A.
235:deltahedron
233:A toroidal
204:tetrahedron
61:topological
1272:p. 60
844:References
794:stephanoid
519:tetrahedra
481:tetrahedra
471:Polyhedra
327:Polyhedra
275:deltahedra
45:polyhedron
1297:MathWorld
1126:: 322–339
1102:2099/1038
1096:: 69–80,
1015:: 140–142
992:1715-0868
904:117884274
810:self-dual
806:isohedral
619:Vertices
344:Vertices
338:octahedra
1330:Category
1253:(1994),
1158:, p. 60.
1072:15911143
920:(1979),
816:See also
802:isogonal
243:coplanar
149:, where
112:embedded
92:manifold
88:polygons
37:geometry
1186:2001419
937:0621628
896:1468859
212:theorem
145:= 2 − 2
72:Császár
55:-holed
1209:
1184:
1145:Usenet
1070:
1060:
990:
935:
902:
894:
677:Faces
648:Edges
410:Image
366:Faces
355:Edges
308:Image
49:toroid
1147:group
1068:S2CID
1040:arXiv
925:(PDF)
900:S2CID
798:noble
557:cubes
546:cubes
535:cubes
384:Genus
297:Genus
105:torus
64:genus
57:torus
43:is a
25:torus
1207:ISBN
1058:ISBN
988:ISSN
672:168
198:The
97:link
74:and
39:, a
1263:doi
1098:hdl
1050:doi
978:doi
884:doi
792:or
701:76
669:168
666:168
663:144
660:168
643:72
555:12
544:12
533:12
507:24
405:11
372:48
361:72
350:24
51:(a
35:In
29:net
1332::
1294:.
1257:,
1182:MR
1178:11
1176:,
1172:,
1141:,
1124:24
1094:13
1092:,
1066:,
1056:,
1048:,
1013:13
1011:,
986:,
972:,
933:MR
927:,
898:,
892:MR
890:,
880:67
878:,
858:;
812:.
788:A
764:.
698:84
695:88
692:68
689:86
686:38
683:30
680:32
657:72
654:60
651:64
640:72
637:72
634:72
631:62
628:30
625:30
622:32
566:8
561:6
550:6
539:8
528:4
523:6
517:8
512:6
501:6
496:4
490:6
485:6
479:8
474:4
393:11
369:36
358:84
347:48
336:8
330:6
303:1
141:+
137:−
107:.
78:.
1300:.
1274:.
1265::
1216:.
1189:.
1105:.
1100::
1075:.
1052::
1042::
1017:.
980::
974:4
940:.
907:.
886::
784:.
402:7
399:5
396:3
390:3
387:1
300:1
151:g
147:g
143:F
139:E
135:V
68:g
66:(
53:g
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.