106:
20:
1571:
1049:
849:
140:. Conversely, any two pairs of points defining a tetrahedron of nonzero volume also define a pair of skew lines. Therefore, a test of whether two pairs of points define skew lines is to apply the formula for the volume of a tetrahedron in terms of its four vertices. Denoting one point as the 1×3 vector
86:
define a pair of skew lines. After the first three points have been chosen, the fourth point will define a non-skew line if, and only if, it is coplanar with the first three points. However, the plane through the first three points forms a subset of measure zero of the cube, and the probability that
1534:
if it is possible to continuously transform one configuration into the other, maintaining throughout the transformation the invariant that all pairs of lines remain skew. Any two configurations of two lines are easily seen to be isotopic, and configurations of the same number of lines in dimensions
1645:
of this ruled surface produces a surface which in general has an elliptical cross-section rather than the circular cross-section produced by rotating L around L'; such surfaces are also called hyperboloids of one sheet, and again are ruled by two families of mutually skew lines. A third type of
1421:
912:
712:
475:
399:
1650:. Like the hyperboloid of one sheet, the hyperbolic paraboloid has two families of skew lines; in each of the two families the lines are parallel to a common plane although not to each other. Any three skew lines in
904:
701:
595:
1494:
1177:
1227:
1272:
301:
90:
Similarly, in three-dimensional space a very small perturbation of any two parallel or intersecting lines will almost certainly turn them into skew lines. Therefore, any four points in
1535:
higher than three are always isotopic, but there exist multiple non-isotopic configurations of three or more lines in three dimensions. The number of nonisotopic configurations of
1357:
1115:
1086:
649:
540:
511:
1044:{\displaystyle \mathbf {c_{2}} =\mathbf {p_{2}} +{\frac {(\mathbf {p_{1}} -\mathbf {p_{2}} )\cdot \mathbf {n_{1}} }{\mathbf {d_{2}} \cdot \mathbf {n_{1}} }}\mathbf {d_{2}} }
844:{\displaystyle \mathbf {c_{1}} =\mathbf {p_{1}} +{\frac {(\mathbf {p_{2}} -\mathbf {p_{1}} )\cdot \mathbf {n_{2}} }{\mathbf {d_{1}} \cdot \mathbf {n_{2}} }}\mathbf {d_{1}} }
620:
1313:
405:
329:
706:
Therefore, the intersecting point of Line 1 with the above-mentioned plane, which is also the point on Line 1 that is nearest to Line 2 is given by
1994:
G. Gallucci (1906), "Studio della figura delle otto rette e sue applicazioni alla geometria del tetraedro ed alla teoria della configurazioni",
857:
654:
548:
1662:
If three skew lines all meet three other skew lines, any transversal of the first set of three meets any transversal of the second set.
1436:
58:. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more
1123:
1558:
1188:
312:
318:
1233:
194:
1516:
1857:
2050:
1957:
75:
2060:
1634:
from it but with the opposite angle that form the opposite regulus. The two reguli display the hyperboloid as a
1610:. For instance, the three hyperboloids visible in the illustration can be formed in this way by rotating a line
114:
1972:
2055:
2045:
87:
the fourth point lies on this plane is zero. If it does not, the lines defined by the points will be skew.
1862:
1416:{\displaystyle \mathbf {n} ={\frac {\mathbf {b} \times \mathbf {d} }{|\mathbf {b} \times \mathbf {d} |}}}
35:
23:
1091:
1062:
625:
516:
487:
97:
In this sense, skew lines are the "usual" case, and parallel or intersecting lines are special cases.
2065:
1607:
603:
1182:
The distance between nearest points in two skew lines may also be expressed using other vectors:
1530:
of skew lines is a set of lines in which all pairs are skew. Two configurations are said to be
1427:
47:
1298:
1647:
1642:
1599:
109:
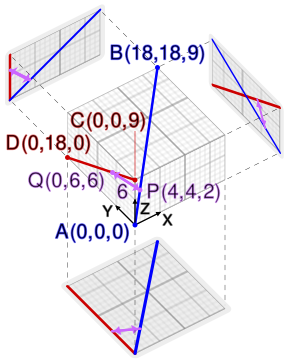
PQ, the shortest distance between two skew lines AB and CD is perpendicular to both AB and CD
54:. A simple example of a pair of skew lines is the pair of lines through opposite edges of a
1980:
1719:. As with lines in 3-space, skew flats are those that are neither parallel nor intersect.
8:
1945:
1731:
470:{\displaystyle {\text{Line 2:}}\;\mathbf {v_{2}} =\mathbf {p_{2}} +t_{2}\mathbf {d_{2}} }
394:{\displaystyle {\text{Line 1:}}\;\mathbf {v_{1}} =\mathbf {p_{1}} +t_{1}\mathbf {d_{1}} }
128:
that it passes through, then these four points must not be coplanar, so they must be the
55:
51:
1925:
1887:
1623:
2018:
1953:
1883:
129:
146:
whose three elements are the point's three coordinate values, and likewise denoting
1579:
125:
91:
1723:
1671:
43:
2022:
1626:; the hyperboloid also contains a second family of lines that are also skew to
105:
1734:, parallelism does not exist; two flats must either intersect or be skew. Let
1315:
determining where the point is on the line, and similarly for arbitrary point
2039:
1941:
1635:
1337:
1295:
representing the direction of the line and with the value of the real number
481:
83:
19:
1908:
1575:
1583:
1349:
133:
1929:
1570:
2027:
1892:
188:
by seeing if the tetrahedron volume formula gives a non-zero result:
59:
899:{\displaystyle \mathbf {n_{1}} =\mathbf {d_{1}} \times \mathbf {n} }
854:
Similarly, the point on Line 2 nearest to Line 1 is given by (where
696:{\displaystyle \mathbf {n_{2}} =\mathbf {d_{2}} \times \mathbf {n} }
590:{\displaystyle \mathbf {n} =\mathbf {d_{1}} \times \mathbf {d_{2}} }
1283:
represents an arbitrary point on the line through particular point
63:
1507:| is zero the lines are parallel and this method cannot be used).
1489:{\displaystyle d=|\mathbf {n} \cdot (\mathbf {c} -\mathbf {a} )|.}
1172:{\displaystyle d=\Vert \mathbf {c_{1}} -\mathbf {c_{2}} \Vert .}
1222:{\displaystyle \mathbf {x} =\mathbf {a} +\lambda \mathbf {b} ;}
137:
1996:
Rendiconto dell'Accademia della
Scienza Fisiche e Matematiche
26:. The line through segment AD and the line through segment B
1881:
1553:
1267:{\displaystyle \mathbf {y} =\mathbf {c} +\mu \mathbf {d} .}
79:
1730:, two flats of any dimension may be parallel. However, in
1117:
form the shortest line segment joining Line 1 and Line 2:
313:
Line–line intersection § Nearest points to skew lines
1654:
lie on exactly one ruled surface of one of these types.
296:{\displaystyle V={\frac {1}{6}}\left|\det \left\right|.}
30:
B are skew lines because they are not in the same plane.
319:
Triangulation (computer vision) § Mid-point method
164:
for the other points, we can check if the line through
124:
If each line in a pair of skew lines is defined by two
227:
1439:
1360:
1301:
1236:
1191:
1126:
1094:
1065:
915:
860:
715:
657:
628:
606:
600:
The plane formed by the translations of Line 2 along
551:
519:
490:
408:
332:
197:
2016:
1940:
1934:
1665:
1488:
1415:
1307:
1266:
1221:
1171:
1109:
1080:
1043:
898:
843:
695:
643:
614:
589:
534:
505:
469:
393:
295:
1682:-flat. Thus, a line may also be called a 1-flat.
1517:Line–line intersection § More than two lines
62:. Two lines are skew if and only if they are not
2037:
219:
1907:Viro, Julia Drobotukhina; Viro, Oleg (1990),
1163:
1133:
1993:
414:
338:
1952:(2nd ed.), Chelsea, pp. 13–17,
1348:is perpendicular to the lines, as is the
1906:
1900:
1569:
104:
18:
1971:
1614:around the central white vertical line
119:
2038:
1987:
1965:
1598:skew but not perpendicular to it, the
1510:
115:Line–line intersection § Formulas
2017:
1882:
1875:
1657:
1551:1, 1, 2, 3, 7, 19, 74, ... (sequence
1321:on the line through particular point
323:Expressing the two lines as vectors:
74:If four points are chosen at random
1858:Distance between two parallel lines
69:
13:
14:
2077:
2010:
1565:
1521:
306:
1471:
1463:
1452:
1401:
1393:
1381:
1373:
1362:
1257:
1246:
1238:
1212:
1201:
1193:
1157:
1153:
1142:
1138:
1110:{\displaystyle \mathbf {c_{2}} }
1101:
1097:
1081:{\displaystyle \mathbf {c_{1}} }
1072:
1068:
1035:
1031:
1020:
1016:
1005:
1001:
991:
987:
973:
969:
958:
954:
937:
933:
922:
918:
892:
882:
878:
867:
863:
835:
831:
820:
816:
805:
801:
791:
787:
773:
769:
758:
754:
737:
733:
722:
718:
689:
679:
675:
664:
660:
644:{\displaystyle \mathbf {p_{2}} }
635:
631:
608:
581:
577:
566:
562:
553:
535:{\displaystyle \mathbf {d_{2}} }
526:
522:
506:{\displaystyle \mathbf {d_{1}} }
497:
493:
461:
457:
436:
432:
421:
417:
385:
381:
360:
356:
345:
341:
273:
265:
256:
248:
239:
231:
1670:In higher-dimensional space, a
1666:Skew flats in higher dimensions
542:is perpendicular to the lines.
1924:. Revised version in English:
1909:"Configurations of skew lines"
1479:
1475:
1459:
1447:
1406:
1388:
979:
949:
779:
749:
1:
1868:
1950:Geometry and the Imagination
1685:Generalizing the concept of
615:{\displaystyle \mathbf {n} }
176:is skew to the line through
7:
1851:
1740:be the set of points on an
1622:within this surface form a
1054:
100:
16:Lines not in the same plane
10:
2082:
1750:be the set of points on a
1514:
1430:between the lines is then
316:
310:
112:
36:three-dimensional geometry
24:Rectangular parallelepiped
1772:then the intersection of
2051:Euclidean solid geometry
1977:Introduction to Geometry
1630:at the same distance as
1608:hyperboloid of one sheet
1582:by skew lines on nested
1308:{\displaystyle \lambda }
651:and is perpendicular to
94:always form skew lines.
1863:Petersen–Morley theorem
1803:In either geometry, if
1693:-dimensional space, an
2061:Orientation (geometry)
1590:If one rotates a line
1587:
1490:
1428:perpendicular distance
1417:
1309:
1268:
1223:
1173:
1111:
1082:
1045:
900:
845:
697:
645:
616:
591:
536:
507:
471:
395:
297:
110:
31:
1981:John Wiley & Sons
1826:, then the points of
1754:-flat. In projective
1648:hyperbolic paraboloid
1646:ruled surface is the
1643:affine transformation
1600:surface of revolution
1573:
1491:
1418:
1310:
1269:
1224:
1174:
1112:
1083:
1046:
901:
846:
698:
646:
617:
592:
537:
508:
472:
396:
298:
113:Further information:
108:
22:
1946:Cohn-Vossen, Stephan
1888:"Line-Line Distance"
1678:is referred to as a
1594:around another line
1437:
1358:
1299:
1277:Here the 1×3 vector
1234:
1189:
1124:
1092:
1063:
913:
858:
713:
655:
626:
604:
549:
517:
488:
406:
330:
195:
120:Testing for skewness
2056:Multilinear algebra
2046:Elementary geometry
1800:-flat is a point.)
1511:More than two lines
1059:The nearest points
622:contains the point
56:regular tetrahedron
2019:Weisstein, Eric W.
1916:Leningrad Math. J.
1884:Weisstein, Eric W.
1658:Gallucci's theorem
1588:
1486:
1413:
1305:
1264:
1219:
1169:
1107:
1078:
1041:
896:
841:
693:
641:
612:
587:
532:
503:
467:
391:
293:
279:
111:
32:
1973:Coxeter, H. S. M.
1411:
1027:
827:
412:
336:
212:
2073:
2032:
2031:
2004:
2003:
1991:
1985:
1984:
1979:(2nd ed.),
1969:
1963:
1962:
1938:
1932:
1923:
1913:
1904:
1898:
1897:
1896:
1879:
1835:
1825:
1814:
1808:
1784:must contain a (
1783:
1777:
1771:
1749:
1739:
1732:projective space
1718:
1618:. The copies of
1580:projective space
1556:
1495:
1493:
1492:
1487:
1482:
1474:
1466:
1455:
1450:
1422:
1420:
1419:
1414:
1412:
1410:
1409:
1404:
1396:
1391:
1385:
1384:
1376:
1370:
1365:
1332:
1326:
1320:
1314:
1312:
1311:
1306:
1294:
1288:
1282:
1273:
1271:
1270:
1265:
1260:
1249:
1241:
1228:
1226:
1225:
1220:
1215:
1204:
1196:
1178:
1176:
1175:
1170:
1162:
1161:
1160:
1147:
1146:
1145:
1116:
1114:
1113:
1108:
1106:
1105:
1104:
1087:
1085:
1084:
1079:
1077:
1076:
1075:
1050:
1048:
1047:
1042:
1040:
1039:
1038:
1028:
1026:
1025:
1024:
1023:
1010:
1009:
1008:
997:
996:
995:
994:
978:
977:
976:
963:
962:
961:
947:
942:
941:
940:
927:
926:
925:
905:
903:
902:
897:
895:
887:
886:
885:
872:
871:
870:
850:
848:
847:
842:
840:
839:
838:
828:
826:
825:
824:
823:
810:
809:
808:
797:
796:
795:
794:
778:
777:
776:
763:
762:
761:
747:
742:
741:
740:
727:
726:
725:
702:
700:
699:
694:
692:
684:
683:
682:
669:
668:
667:
650:
648:
647:
642:
640:
639:
638:
621:
619:
618:
613:
611:
596:
594:
593:
588:
586:
585:
584:
571:
570:
569:
556:
541:
539:
538:
533:
531:
530:
529:
512:
510:
509:
504:
502:
501:
500:
476:
474:
473:
468:
466:
465:
464:
454:
453:
441:
440:
439:
426:
425:
424:
413:
410:
400:
398:
397:
392:
390:
389:
388:
378:
377:
365:
364:
363:
350:
349:
348:
337:
334:
302:
300:
299:
294:
289:
285:
284:
280:
276:
268:
259:
251:
242:
234:
213:
205:
187:
181:
175:
169:
163:
157:
151:
145:
92:general position
70:General position
2081:
2080:
2076:
2075:
2074:
2072:
2071:
2070:
2066:Line (geometry)
2036:
2035:
2013:
2008:
2007:
1992:
1988:
1970:
1966:
1960:
1939:
1935:
1930:math.GT/0611374
1911:
1905:
1901:
1880:
1876:
1871:
1854:
1827:
1820:
1815:intersect at a
1810:
1804:
1779:
1773:
1759:
1745:
1744:-flat, and let
1735:
1706:
1668:
1660:
1568:
1552:
1524:
1519:
1513:
1478:
1470:
1462:
1451:
1446:
1438:
1435:
1434:
1405:
1400:
1392:
1387:
1386:
1380:
1372:
1371:
1369:
1361:
1359:
1356:
1355:
1328:
1322:
1316:
1300:
1297:
1296:
1290:
1284:
1278:
1256:
1245:
1237:
1235:
1232:
1231:
1211:
1200:
1192:
1190:
1187:
1186:
1156:
1152:
1151:
1141:
1137:
1136:
1125:
1122:
1121:
1100:
1096:
1095:
1093:
1090:
1089:
1071:
1067:
1066:
1064:
1061:
1060:
1057:
1034:
1030:
1029:
1019:
1015:
1014:
1004:
1000:
999:
998:
990:
986:
985:
972:
968:
967:
957:
953:
952:
948:
946:
936:
932:
931:
921:
917:
916:
914:
911:
910:
891:
881:
877:
876:
866:
862:
861:
859:
856:
855:
834:
830:
829:
819:
815:
814:
804:
800:
799:
798:
790:
786:
785:
772:
768:
767:
757:
753:
752:
748:
746:
736:
732:
731:
721:
717:
716:
714:
711:
710:
688:
678:
674:
673:
663:
659:
658:
656:
653:
652:
634:
630:
629:
627:
624:
623:
607:
605:
602:
601:
580:
576:
575:
565:
561:
560:
552:
550:
547:
546:
525:
521:
520:
518:
515:
514:
496:
492:
491:
489:
486:
485:
460:
456:
455:
449:
445:
435:
431:
430:
420:
416:
415:
409:
407:
404:
403:
384:
380:
379:
373:
369:
359:
355:
354:
344:
340:
339:
333:
331:
328:
327:
321:
315:
309:
278:
277:
272:
264:
261:
260:
255:
247:
244:
243:
238:
230:
226:
222:
218:
214:
204:
196:
193:
192:
183:
177:
171:
165:
159:
153:
147:
141:
122:
117:
103:
72:
29:
17:
12:
11:
5:
2079:
2069:
2068:
2063:
2058:
2053:
2048:
2034:
2033:
2012:
2011:External links
2009:
2006:
2005:
1998:, 3rd series,
1986:
1964:
1958:
1942:Hilbert, David
1933:
1922:(4): 1027–1050
1918:(in Russian),
1899:
1873:
1872:
1870:
1867:
1866:
1865:
1860:
1853:
1850:
1667:
1664:
1659:
1656:
1567:
1566:Ruled surfaces
1564:
1563:
1562:
1543:, starting at
1523:
1522:Configurations
1520:
1512:
1509:
1497:
1496:
1485:
1481:
1477:
1473:
1469:
1465:
1461:
1458:
1454:
1449:
1445:
1442:
1424:
1423:
1408:
1403:
1399:
1395:
1390:
1383:
1379:
1375:
1368:
1364:
1304:
1275:
1274:
1263:
1259:
1255:
1252:
1248:
1244:
1240:
1229:
1218:
1214:
1210:
1207:
1203:
1199:
1195:
1180:
1179:
1168:
1165:
1159:
1155:
1150:
1144:
1140:
1135:
1132:
1129:
1103:
1099:
1074:
1070:
1056:
1053:
1052:
1051:
1037:
1033:
1022:
1018:
1013:
1007:
1003:
993:
989:
984:
981:
975:
971:
966:
960:
956:
951:
945:
939:
935:
930:
924:
920:
894:
890:
884:
880:
875:
869:
865:
852:
851:
837:
833:
822:
818:
813:
807:
803:
793:
789:
784:
781:
775:
771:
766:
760:
756:
751:
745:
739:
735:
730:
724:
720:
691:
687:
681:
677:
672:
666:
662:
637:
633:
610:
598:
597:
583:
579:
574:
568:
564:
559:
555:
528:
524:
499:
495:
478:
477:
463:
459:
452:
448:
444:
438:
434:
429:
423:
419:
401:
387:
383:
376:
372:
368:
362:
358:
353:
347:
343:
308:
307:Nearest points
305:
304:
303:
292:
288:
283:
275:
271:
267:
263:
262:
258:
254:
250:
246:
245:
241:
237:
233:
229:
228:
225:
221:
217:
211:
208:
203:
200:
121:
118:
102:
99:
78:within a unit
71:
68:
27:
15:
9:
6:
4:
3:
2:
2078:
2067:
2064:
2062:
2059:
2057:
2054:
2052:
2049:
2047:
2044:
2043:
2041:
2030:
2029:
2024:
2020:
2015:
2014:
2001:
1997:
1990:
1983:, p. 257
1982:
1978:
1974:
1968:
1961:
1959:0-8284-1087-9
1955:
1951:
1947:
1943:
1937:
1931:
1927:
1921:
1917:
1910:
1903:
1895:
1894:
1889:
1885:
1878:
1874:
1864:
1861:
1859:
1856:
1855:
1849:
1847:
1843:
1839:
1836:determine a (
1834:
1830:
1823:
1818:
1813:
1807:
1801:
1799:
1795:
1791:
1787:
1782:
1776:
1770:
1766:
1762:
1757:
1753:
1748:
1743:
1738:
1733:
1729:
1727:
1720:
1717:
1713:
1709:
1704:
1701:-flat may be
1700:
1696:
1692:
1688:
1683:
1681:
1677:
1674:of dimension
1673:
1663:
1655:
1653:
1649:
1644:
1639:
1637:
1636:ruled surface
1633:
1629:
1625:
1621:
1617:
1613:
1609:
1605:
1602:swept out by
1601:
1597:
1593:
1585:
1581:
1577:
1572:
1560:
1555:
1550:
1549:
1548:
1546:
1542:
1538:
1533:
1529:
1528:configuration
1518:
1508:
1506:
1502:
1483:
1467:
1456:
1443:
1440:
1433:
1432:
1431:
1429:
1397:
1377:
1366:
1354:
1353:
1352:
1351:
1347:
1343:
1339:
1338:cross product
1334:
1331:
1327:in direction
1325:
1319:
1302:
1293:
1287:
1281:
1261:
1253:
1250:
1242:
1230:
1216:
1208:
1205:
1197:
1185:
1184:
1183:
1166:
1148:
1130:
1127:
1120:
1119:
1118:
1011:
982:
964:
943:
928:
909:
908:
907:
888:
873:
811:
782:
764:
743:
728:
709:
708:
707:
704:
685:
670:
572:
557:
545:
544:
543:
483:
482:cross product
450:
446:
442:
427:
402:
374:
370:
366:
351:
326:
325:
324:
320:
314:
290:
286:
281:
269:
252:
235:
223:
215:
209:
206:
201:
198:
191:
190:
189:
186:
180:
174:
168:
162:
156:
150:
144:
139:
135:
131:
127:
116:
107:
98:
95:
93:
88:
85:
84:almost surely
81:
77:
67:
65:
61:
57:
53:
49:
45:
41:
37:
25:
21:
2026:
2023:"Skew Lines"
1999:
1995:
1989:
1976:
1967:
1949:
1936:
1919:
1915:
1902:
1891:
1877:
1845:
1841:
1837:
1832:
1828:
1821:
1816:
1811:
1805:
1802:
1797:
1793:
1789:
1785:
1780:
1774:
1768:
1764:
1760:
1755:
1751:
1746:
1741:
1736:
1725:
1721:
1715:
1711:
1707:
1702:
1698:
1697:-flat and a
1694:
1690:
1686:
1684:
1679:
1675:
1669:
1661:
1651:
1640:
1631:
1627:
1619:
1615:
1611:
1603:
1595:
1591:
1589:
1584:hyperboloids
1544:
1540:
1536:
1531:
1527:
1525:
1504:
1500:
1498:
1425:
1345:
1341:
1335:
1329:
1323:
1317:
1291:
1285:
1279:
1276:
1181:
1058:
853:
705:
599:
479:
322:
184:
178:
172:
166:
160:
154:
148:
142:
123:
96:
89:
82:, they will
73:
50:and are not
46:that do not
39:
33:
1819:-flat, for
1796:)-flat. (A
1758:-space, if
1350:unit vector
136:of nonzero
134:tetrahedron
2040:Categories
1869:References
1687:skew lines
1515:See also:
317:See also:
311:See also:
60:dimensions
40:skew lines
2028:MathWorld
1893:MathWorld
1576:fibration
1539:lines in
1468:−
1457:⋅
1398:×
1378:×
1303:λ
1254:μ
1209:λ
1164:‖
1149:−
1134:‖
1012:⋅
983:⋅
965:−
889:×
812:⋅
783:⋅
765:−
686:×
573:×
270:−
253:−
236:−
76:uniformly
48:intersect
1975:(1969),
1948:(1952),
1852:See also
1848:)-flat.
1547:= 1, is
1532:isotopic
1055:Distance
130:vertices
101:Formulas
64:coplanar
52:parallel
42:are two
2002:: 49–79
1844:−
1792:−
1724:affine
1624:regulus
1557:in the
1554:A110887
411:Line 2:
335:Line 1:
1956:
1728:-space
158:, and
138:volume
126:points
1926:arXiv
1912:(PDF)
1714:<
1606:is a
1499:(if |
1289:with
132:of a
44:lines
1954:ISBN
1809:and
1778:and
1705:if
1703:skew
1672:flat
1559:OEIS
1426:The
1344:and
1336:The
1088:and
513:and
480:The
182:and
170:and
80:cube
1824:≥ 0
1722:In
1689:to
1641:An
1578:of
1340:of
484:of
220:det
34:In
2042::
2025:,
2021:,
2000:12
1944:;
1914:,
1890:,
1886:,
1831:∪
1767:≥
1763:+
1710:+
1638:.
1574:A
1561:).
1526:A
1503:×
1333:.
906:)
703:.
152:,
66:.
38:,
1928::
1920:1
1846:k
1842:j
1840:+
1838:i
1833:J
1829:I
1822:k
1817:k
1812:J
1806:I
1798:0
1794:d
1790:j
1788:+
1786:i
1781:J
1775:I
1769:d
1765:j
1761:i
1756:d
1752:j
1747:J
1742:i
1737:I
1726:d
1716:d
1712:j
1708:i
1699:j
1695:i
1691:d
1680:k
1676:k
1652:R
1632:L
1628:M
1620:L
1616:M
1612:L
1604:L
1596:M
1592:L
1586:.
1545:n
1541:R
1537:n
1505:d
1501:b
1484:.
1480:|
1476:)
1472:a
1464:c
1460:(
1453:n
1448:|
1444:=
1441:d
1407:|
1402:d
1394:b
1389:|
1382:d
1374:b
1367:=
1363:n
1346:d
1342:b
1330:d
1324:c
1318:y
1292:b
1286:a
1280:x
1262:.
1258:d
1251:+
1247:c
1243:=
1239:y
1217:;
1213:b
1206:+
1202:a
1198:=
1194:x
1167:.
1158:2
1154:c
1143:1
1139:c
1131:=
1128:d
1102:2
1098:c
1073:1
1069:c
1036:2
1032:d
1021:1
1017:n
1006:2
1002:d
992:1
988:n
980:)
974:2
970:p
959:1
955:p
950:(
944:+
938:2
934:p
929:=
923:2
919:c
893:n
883:1
879:d
874:=
868:1
864:n
836:1
832:d
821:2
817:n
806:1
802:d
792:2
788:n
780:)
774:1
770:p
759:2
755:p
750:(
744:+
738:1
734:p
729:=
723:1
719:c
690:n
680:2
676:d
671:=
665:2
661:n
636:2
632:p
609:n
582:2
578:d
567:1
563:d
558:=
554:n
527:2
523:d
498:1
494:d
462:2
458:d
451:2
447:t
443:+
437:2
433:p
428:=
422:2
418:v
386:1
382:d
375:1
371:t
367:+
361:1
357:p
352:=
346:1
342:v
291:.
287:|
282:]
274:d
266:c
257:c
249:b
240:b
232:a
224:[
216:|
210:6
207:1
202:=
199:V
185:d
179:c
173:b
167:a
161:d
155:c
149:b
143:a
28:1
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.