27:
313:
164:
In a directed acyclic graph, if there is at most one directed path between any two vertices, or equivalently if the subgraph reachable from any vertex induces an undirected tree, then its
206:
156:
may contain multiple marriages from one family to another, but does not contain marriages between any two blood relatives, then it forms a multitree.
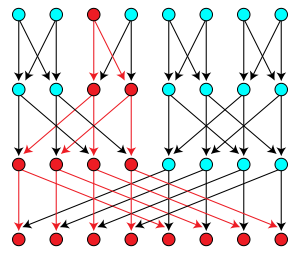
34:, a multitree used in distributed computation, showing in red the undirected tree induced by the subgraph reachable from one of its vertices.
346:
553:
418:
Algorithms and
Computation, 7th International Symposium, ISAAC '96, Osaka, Japan, December 16–18, 1996, Proceedings
130:
172:
identifies a directed acyclic graph in which the subgraph reachable from any vertex induces an undirected tree.
308:{\displaystyle 2\leq \lim _{n\to \infty }D(n){\Big /}{\binom {n}{\lfloor n/2\rfloor }}\leq 2{\frac {3}{11}}}
59:
339:
332:
142:
475:
McGuffin, Michael J.; Balakrishnan, Ravin (2005), "Interactive visualization of genealogical graphs",
246:
51:
548:
342:
rooted in the vertex, that is a polytree in which all edges are oriented away from the root.
67:
55:
529:
383:
169:
168:
relation is a diamond-free partial order. Conversely, in a diamond-free partial order, the
8:
63:
420:, Lecture Notes in Computer Science, vol. 1178, Springer-Verlag, pp. 193–202,
387:
506:
Jung, H. A. (1978), "On a class of posets and the corresponding comparability graphs",
488:
457:
373:
149:
520:
31:
492:
461:
515:
480:
447:
421:
442:; Zacks, Jeff (1994), "Multitrees: enriching and reusing hierarchical structure",
525:
181:
542:
439:
401:
39:
484:
145:
in which there is at most one computational path connecting any two states.
165:
43:
452:
153:
444:
Proc. SIGCHI conference on Human
Factors in Computing Systems (CHI '94)
425:
26:
20:
196:) denotes the largest possible diamond-free family of subsets of an
335:
the edges of an undirected tree, is a special case of a multitree.
328:
16:
Directed acyclic graph with ≤1 directed paths between any two nodes
479:, Los Alamitos, California, US: IEEE Computer Society, p. 3,
378:
54:(DAG) in which there is at most one directed path between any two
188:
of sets whose inclusion ordering forms a diamond-free poset. If
159:
349:, or to other structures formed by combining multiple trees.
338:
The subgraph reachable from any vertex in a multitree is an
148:
Multitrees may be used to represent multiple overlapping
368:
Griggs, Jerrold R.; Li, Wei-Tian; Lu, Linyuan (2010),
345:
The word "multitree" has also been used to refer to a
209:
474:
50:
may describe either of two equivalent structures: a
307:
283:
254:
540:
217:
400:
160:Equivalence between DAG and poset definitions
277:
263:
477:IEEE Symposium on Information Visualization
438:
319:and it is conjectured that the limit is 2.
404:; Lange, Klaus-Jörn (1996), "StUSPACE(log
367:
122:incomparable to each other (also called a
519:
508:Journal of Combinatorial Theory, Series B
451:
377:
175:
25:
541:
70:(poset) that does not have four items
363:
361:
331:, a directed acyclic graph formed by
322:
62:reachable from any vertex induces an
505:
200:-element set, then it is known that
133:, multitrees have also been called
13:
358:
258:
227:
14:
565:
86:forming a diamond suborder with
152:over the same ground set. If a
131:computational complexity theory
58:, or equivalently in which the
499:
468:
432:
394:
241:
235:
224:
1:
352:
347:series–parallel partial order
521:10.1016/0095-8956(78)90013-8
141:; they can be used to model
7:
143:nondeterministic algorithms
135:strongly unambiguous graphs
10:
570:
18:
19:Not to be confused with
554:Directed acyclic graphs
485:10.1109/INFOVIS.2005.22
309:
52:directed acyclic graph
35:
453:10.1145/191666.191778
370:Diamond-free families
310:
176:Diamond-free families
68:partially ordered set
29:
446:, pp. 330–336,
207:
170:transitive reduction
388:2010arXiv1010.5311G
426:10.1007/BFb0009495
323:Related structures
305:
231:
124:diamond-free poset
36:
440:Furnas, George W.
303:
281:
216:
32:butterfly network
561:
534:
532:
523:
503:
497:
495:
472:
466:
464:
455:
436:
430:
428:
398:
392:
390:
381:
365:
314:
312:
311:
306:
304:
296:
288:
287:
286:
280:
273:
257:
250:
249:
230:
121:
117:
113:
99:
85:
81:
77:
73:
569:
568:
564:
563:
562:
560:
559:
558:
539:
538:
537:
504:
500:
473:
469:
437:
433:
408:) ⊆ DSPACE(log
399:
395:
366:
359:
355:
325:
295:
282:
269:
262:
253:
252:
251:
245:
244:
220:
208:
205:
204:
180:A diamond-free
178:
162:
119:
115:
101:
87:
83:
79:
75:
71:
64:undirected tree
24:
17:
12:
11:
5:
567:
557:
556:
551:
536:
535:
514:(2): 125–133,
498:
467:
431:
402:Allender, Eric
393:
356:
354:
351:
324:
321:
317:
316:
302:
299:
294:
291:
285:
279:
276:
272:
268:
265:
261:
256:
248:
243:
240:
237:
234:
229:
226:
223:
219:
215:
212:
182:family of sets
177:
174:
161:
158:
15:
9:
6:
4:
3:
2:
566:
555:
552:
550:
547:
546:
544:
531:
527:
522:
517:
513:
509:
502:
494:
490:
486:
482:
478:
471:
463:
459:
454:
449:
445:
441:
435:
427:
423:
419:
415:
411:
407:
403:
397:
389:
385:
380:
375:
371:
364:
362:
357:
350:
348:
343:
341:
336:
334:
330:
320:
300:
297:
292:
289:
274:
270:
266:
259:
238:
232:
221:
213:
210:
203:
202:
201:
199:
195:
191:
187:
183:
173:
171:
167:
157:
155:
151:
146:
144:
140:
136:
132:
127:
125:
112:
108:
104:
98:
94:
90:
69:
65:
61:
57:
53:
49:
45:
41:
40:combinatorics
33:
28:
22:
549:Order theory
511:
507:
501:
476:
470:
443:
434:
417:
413:
409:
405:
396:
369:
344:
340:arborescence
337:
326:
318:
197:
193:
189:
185:
184:is a family
179:
166:reachability
163:
147:
138:
134:
128:
123:
110:
106:
102:
96:
92:
88:
47:
44:order theory
37:
154:family tree
543:Categories
353:References
150:taxonomies
412:/log log
379:1010.5311
333:orienting
290:≤
278:⌋
264:⌊
228:∞
225:→
214:≤
139:mangroves
114:but with
48:multitree
21:MultiTree
493:15449409
462:18710118
329:polytree
60:subgraph
56:vertices
530:0491356
384:Bibcode
66:, or a
528:
491:
460:
82:, and
489:S2CID
458:S2CID
374:arXiv
416:)",
118:and
100:and
46:, a
42:and
30:The
516:doi
481:doi
448:doi
422:doi
218:lim
137:or
129:In
126:).
38:In
545::
526:MR
524:,
512:24
510:,
487:,
456:,
382:,
372:,
360:^
327:A
301:11
109:≤
105:≤
95:≤
91:≤
78:,
74:,
533:.
518::
496:.
483::
465:.
450::
429:.
424::
414:n
410:n
406:n
391:.
386::
376::
315:,
298:3
293:2
284:)
275:2
271:/
267:n
260:n
255:(
247:/
242:)
239:n
236:(
233:D
222:n
211:2
198:n
194:n
192:(
190:D
186:F
120:c
116:b
111:d
107:c
103:a
97:d
93:b
89:a
84:d
80:c
76:b
72:a
23:.
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.