223:
256:
56:
243:
by folding its two triangles onto each other over their shared diagonal, but this folded placement cannot be obtained by a continuous motion.) Thus, if all squares of the given grid are cross-braced, the grid cannot change shape; its only continuous motions would be to rotate it or translate it as a single
335:
of the bipartite graph, minus one. If a partially braced grid is to be made rigid by cross-bracing more squares, the minimum number of additional squares that need to be cross-braced is this number of degrees of freedom. A solution with this number of squares can be obtained by adding this number of
242:
by adding one of its diagonals as another rigid bar, the diagonal divides it into two triangles which similarly cannot change shape, so the square must remain square through any continuous motion of the cross-braced framework. (The same framework could also be placed in the plane in a different way,
214:
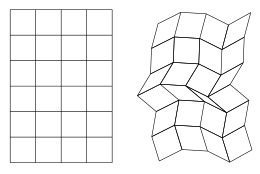
vertices of the grid. A valid continuous motion of this framework is a way of continuously varying the placement of its edges and joints into the plane in such a way that they keep the same lengths and the same attachments, but without requiring them to form squares. Instead, each square of the grid
448:
One can represent a tension bracing by a bipartite graph, which has an edge directed from a row vertex to a column vertex if the shared square of that row and column is braced by the positively-sloped diagonal, and an edge from a column vertex to a row vertex if the shared square is braced by the
445:, in which squares are braced by wires or strings (which cannot expand past their initial length, but can bend or collapse to a shorter length) instead of by rigid rods. To make a single square rigid by tension bracing, it is necessary to brace both of its diagonals, instead of just one diagonal.
283:
that has a vertex for each row and column of the given grid, and an edge for each cross-braced square of the grid. They proved that the cross-braced grid is rigid if and only if this bipartite graph is connected. It follows that the minimal cross-bracings of the grid correspond to the
247:. However, this method of making the grid rigid, by adding cross-braces to all its squares, uses many more cross-braces than necessary. The grid bracing problem asks for a description of the minimal sets of cross-braces that have the same effect, of making the whole framework rigid.
476:
are exactly the bridgeless graphs; reinterpreting this theorem in terms of grid bracing, a bracing by rigid rods forms a double bracing if and only if each of its rods can be replaced by a single wire (possibly on the other diagonal of its square) to form a rigid tension bracing.
349:
Another version of the problem asks for a "double bracing", a set of cross-braces that is sufficiently redundant that it will stay rigid even if one of the diagonals is removed. This version allows both diagonals of a single square to be used, but it is not required to do so.
578:. See in particular sections 1.2 ("The grid bracing problem", pp. 4–12), 1.5 ("More about the grid problem", pp. 19–22), 2.6 ("The solution to the grid problem", pp. 50–55), and 4.4 ("Tensegrity: tension bracings", particularly pp. 158–161).
259:
A rigid cross-braced grid, and the corresponding bipartite graph on vertices representing the rows and columns of the grid. The graph is a tree, so the cross-bracing uses the minimum possible number of braced
234:
Unlike squares, triangles made of rigid rods and flexible joints cannot change their shapes: any two triangles with sides of the same lengths must be congruent (this is the
161:
404:
320:
cross-braced squares. Any overbraced but rigid cross-bracing (with more than this number of cross-braced squares) can be reduced to a minimal cross-bracing by finding a
212:
318:
105:
85:
456:
If a given set of braces is insufficient, additional bracing needs to be added, corresponding in the graph view to adding edges that connect together the
413:. Hamiltonian cycles are easy to find in the complete bipartite graphs representing the bracing problem, but finding them in other bipartite graphs is
515:
336:
edges to the bipartite graph, connecting pairs of its connected components so that after the addition there is only one remaining component.
353:
In the same bipartite graph view used to solve the bracing problem, a double bracing of a grid corresponds to an undirected bipartite
669:
Cheriyan, J.; Sebő, A.; Szigeti, Z. (2001), "Improving on the 1.5-approximation of a smallest 2-edge connected spanning subgraph",
819:
219:, and the whole grid may form an irregular structure with a different shape for each of its faces, as shown in the figure.
409:
In the special case of grids with equal numbers of rows and columns, the only double bracings of this minimum size are
613:
564:
525:
59:
An unbraced square grid with six rows and four columns, and a non-square grid obtained from a continuous motion of it
809:
461:
460:
of a graph. In this way problem of finding a minimal set of additional braces to add can be seen as an instance of
786:
328:
163:
edges, each of which has unit length and is considered to be a rigid rod, free to move continuously within the
608:, Series on Knots and Everything, vol. 25 (2nd ed.), Singapore: World Scientific, pp. 154–159,
747:
559:, The Dolciani Mathematical Expositions, vol. 25, Washington, DC: Mathematical Association of America,
457:
450:
640:
265:
40:
520:, Cambridge Urban and Architectural Studies, Cambridge, UK: Cambridge University Press, pp. 76–87,
473:
708:
332:
110:
35:
to make it into a rigid structure. It can be solved optimally by translating it into a problem in
421:. However, it is possible to approximate this smallest double braced subset to within a constant
368:
167:
but unable to change its length. These rods are attached to each other by flexible joints at the
449:
negatively-sloped diagonal. The braced structure is rigid if and only if the resulting graph is
170:
814:
554:
601:
358:
729:
690:
623:
574:
362:
291:
8:
469:
422:
285:
20:
764:
90:
70:
609:
560:
521:
410:
222:
745:(1939), "A theorem on graphs, with an application to a problem on traffic control",
417:. Because of this, finding the smallest double braced subset of a larger bracing is
272:) originally observed, the grid bracing problem can be translated into a problem in
756:
717:
678:
652:
277:
327:
More generally, suppose that a cross-braced grid is not rigid. Then the number of
742:
725:
706:; Jordán, Tibor (2000), "How to make a square grid framework with cables rigid",
703:
686:
619:
570:
280:
164:
44:
434:
721:
682:
803:
511:
321:
239:
235:
28:
597:
273:
36:
556:
Counting on
Frameworks: Mathematics to Aid the Design of Rigid Structures
465:
414:
64:
32:
768:
354:
244:
760:
656:
437:, was discovered by Jenny Baglivo and Jack Graver (
418:
365:. The minimum number of diagonals needed for a double bracing is
288:
connecting all vertices in the graph, and that they have exactly
227:
216:
472:, the undirected graphs that can be made strongly connected by
255:
55:
16:
Mathematical problem of making a square grid structure rigid
606:
Connections: The
Geometric Bridge Between Art and Science
514:; Graver, Jack E. (1983), "3.10 Bracing structures",
371:
294:
173:
113:
93:
73:
668:
63:The problem considers a framework in the form of a
398:
361:, meaning that every edge belongs to at least one
312:
206:
155:
99:
79:
517:Incidence and Symmetry in Design and Architecture
801:
372:
645:Environment and Planning B: Planning and Design
643:(1977), "How to brace a one-story building",
510:
438:
331:in its family of shapes equals the number of
702:
638:
269:
250:
596:
254:
230:, but a triangle forms a rigid structure
221:
54:
787:"A theorem on rectangular tensegrities"
741:
802:
634:
632:
552:
506:
504:
502:
500:
498:
496:
494:
492:
490:
592:
590:
588:
586:
584:
548:
546:
544:
542:
540:
538:
536:
671:SIAM Journal on Discrete Mathematics
662:
50:
696:
629:
487:
13:
784:
735:
581:
533:
428:
14:
831:
778:
344:
107:columns of squares. The grid has
462:strong connectivity augmentation
264:As Ethan Bolker and
393:
375:
201:
189:
186:
174:
147:
135:
129:
117:
1:
748:American Mathematical Monthly
480:
458:strongly connected components
339:
156:{\displaystyle r(c+1)+(r+1)c}
226:A square can flex to form a
7:
820:Application-specific graphs
433:An analogous theory, using
399:{\displaystyle \min(2r,2c)}
10:
836:
215:may be deformed to form a
207:{\displaystyle (r+1)(c+1)}
722:10.1137/S0097539798347189
709:SIAM Journal on Computing
683:10.1137/S0895480199362071
602:"4.18 Bracing structures"
553:Graver, Jack E. (2001),
251:Graph theoretic solution
810:Mathematics of rigidity
464:, and can be solved in
27:is a problem of adding
400:
357:that is connected and
314:
261:
231:
208:
157:
101:
81:
60:
19:In the mathematics of
474:directing their edges
401:
315:
313:{\displaystyle r+c-1}
258:
225:
209:
158:
102:
82:
58:
369:
333:connected components
292:
171:
111:
91:
71:
423:approximation ratio
21:structural rigidity
794:Theorem of the day
451:strongly connected
411:Hamiltonian cycles
396:
329:degrees of freedom
310:
276:by considering an
262:
238:). If a square is
232:
204:
153:
97:
77:
61:
512:Baglivo, Jenny A.
100:{\displaystyle c}
80:{\displaystyle r}
51:Problem statement
827:
796:
791:
772:
771:
739:
733:
732:
704:Gabow, Harold N.
700:
694:
693:
666:
660:
659:
636:
627:
626:
594:
579:
577:
550:
531:
530:
508:
470:Robbins' theorem
405:
403:
402:
397:
319:
317:
316:
311:
213:
211:
210:
205:
162:
160:
159:
154:
106:
104:
103:
98:
86:
84:
83:
78:
45:bipartite graphs
835:
834:
830:
829:
828:
826:
825:
824:
800:
799:
789:
785:Whitty, Robin,
781:
776:
775:
761:10.2307/2303897
740:
736:
701:
697:
667:
663:
657:10.1068/b040125
639:Bolker, E. D.;
637:
630:
616:
595:
582:
567:
551:
534:
528:
509:
488:
483:
468:. According to
443:tension bracing
435:directed graphs
431:
429:Tension bracing
370:
367:
366:
347:
342:
293:
290:
289:
281:bipartite graph
253:
172:
169:
168:
165:Euclidean plane
112:
109:
108:
92:
89:
88:
72:
69:
68:
53:
17:
12:
11:
5:
833:
823:
822:
817:
812:
798:
797:
780:
779:External links
777:
774:
773:
755:(5): 281–283,
743:Robbins, H. E.
734:
716:(2): 649–680,
695:
677:(2): 170–180,
661:
651:(2): 125–152,
628:
614:
580:
565:
532:
526:
485:
484:
482:
479:
430:
427:
395:
392:
389:
386:
383:
380:
377:
374:
346:
345:Double bracing
343:
341:
338:
324:of its graph.
309:
306:
303:
300:
297:
252:
249:
203:
200:
197:
194:
191:
188:
185:
182:
179:
176:
152:
149:
146:
143:
140:
137:
134:
131:
128:
125:
122:
119:
116:
96:
76:
52:
49:
15:
9:
6:
4:
3:
2:
832:
821:
818:
816:
815:Spanning tree
813:
811:
808:
807:
805:
795:
788:
783:
782:
770:
766:
762:
758:
754:
750:
749:
744:
738:
731:
727:
723:
719:
715:
711:
710:
705:
699:
692:
688:
684:
680:
676:
672:
665:
658:
654:
650:
646:
642:
635:
633:
625:
621:
617:
615:9789810245856
611:
607:
603:
599:
598:Kappraff, Jay
593:
591:
589:
587:
585:
576:
572:
568:
566:0-88385-331-0
562:
558:
557:
549:
547:
545:
543:
541:
539:
537:
529:
527:9780521297844
523:
519:
518:
513:
507:
505:
503:
501:
499:
497:
495:
493:
491:
486:
478:
475:
471:
467:
463:
459:
454:
452:
446:
444:
440:
436:
426:
424:
420:
416:
412:
407:
390:
387:
384:
381:
378:
364:
360:
356:
351:
337:
334:
330:
325:
323:
322:spanning tree
307:
304:
301:
298:
295:
287:
282:
279:
275:
271:
267:
257:
248:
246:
241:
237:
236:SSS postulate
229:
224:
220:
218:
198:
195:
192:
183:
180:
177:
166:
150:
144:
141:
138:
132:
126:
123:
120:
114:
94:
74:
66:
57:
48:
46:
42:
38:
34:
30:
29:cross bracing
26:
22:
793:
752:
746:
737:
713:
707:
698:
674:
670:
664:
648:
644:
605:
555:
516:
455:
447:
442:
432:
408:
352:
348:
326:
274:graph theory
263:
240:cross-braced
233:
62:
41:connectivity
37:graph theory
25:grid bracing
24:
18:
466:linear time
415:NP-complete
266:Henry Crapo
65:square grid
33:square grid
804:Categories
481:References
359:bridgeless
355:multigraph
340:Variations
278:undirected
245:rigid body
641:Crapo, H.
305:−
87:rows and
600:(2001),
260:squares.
769:2303897
730:1769375
691:1856004
624:1868159
575:1843781
419:NP-hard
268: (
228:rhombus
217:rhombus
67:, with
39:on the
767:
728:
689:
622:
612:
573:
563:
524:
441:) for
790:(PDF)
765:JSTOR
363:cycle
286:trees
31:to a
610:ISBN
561:ISBN
522:ISBN
439:1983
270:1977
757:doi
718:doi
679:doi
653:doi
373:min
43:of
806::
792:,
763:,
753:46
751:,
726:MR
724:,
714:30
712:,
687:MR
685:,
675:14
673:,
647:,
631:^
620:MR
618:,
604:,
583:^
571:MR
569:,
535:^
489:^
453:.
425:.
406:.
47:.
23:,
759::
720::
681::
655::
649:4
394:)
391:c
388:2
385:,
382:r
379:2
376:(
308:1
302:c
299:+
296:r
202:)
199:1
196:+
193:c
190:(
187:)
184:1
181:+
178:r
175:(
151:c
148:)
145:1
142:+
139:r
136:(
133:+
130:)
127:1
124:+
121:c
118:(
115:r
95:c
75:r
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.