Curve-shortening flow

1716:, and the update rule depends only on the number of neighbors with each of the two states rather than on any more complicated function of those states. In one particular life-like rule, introduced by Gerard Vichniac and called the twisted majority rule or annealing rule, the update rule sets the new value for each cell to be the majority among the nine cells given by it and its eight neighbors, except when these cells are split among four with one state and five with the other state, in which case the new value of the cell is the minority rather than the majority. The detailed dynamics of this rule are complicated, including the existence of small stable structures. However, in the aggregate (when started with all cells in random states) it tends to form large regions of cells that are all in the same state as each other, with the boundaries between these regions evolving according to the curve-shortening flow. 888:. For such curves, if both sides of the curve have infinite area, then the evolved curve remains smooth and singularity-free for all time. However, if one side of an unbounded curve has finite area, and the curve has finite total absolute curvature, then its evolution reaches a singularity in time proportional to the area on the finite-area side of the curve, with unbounded curvature near the singularity. For curves that are graphs of sufficiently well-behaved functions, asymptotic to a ray in each direction, the solution converges in shape to a unique shape that is asymptotic to the same rays. For networks formed by two disjoint rays on the same line, together with two smooth curves connecting the endpoints of the two rays, an analogue of the Gage–Hamilton–Grayson theorem holds, under which the region between the two curves becomes convex and then converges to a 409:. It is not well defined at points of zero curvature, but the product of the curvature and the normal vector remains well defined at those points, allowing the curve-shortening flow to be defined. Curves in space may cross each other or themselves according to this flow, and the flow may lead to singularities in the curves; every singularity is asymptotic to a plane. However, spherical curves and curves which can be orthogonally projected into a regular convex planar curve are known to remain simple. The curve shortening flow for space curves has been used as a way to define flow past singularities in plane curves. 869: 429: 1672:. They observe that this scale space is invariant under Euclidean transformations of the given shape, and assert that it uniquely determines the shape and is robust against small variations in the shape. They compare it experimentally against several related alternative definitions of a scale space for shapes, and find that the resampled curvature scale space is less computationally intensive, more robust against nonuniform noise, and less strongly influenced by small-scale shape differences. 1011: 33: 1438:, or of shock waves within a single material. These methods involve deriving the equations of motion of the boundary, and using them to directly simulate the motion of the boundary, rather than simulating the underlying fluid and treating the boundary as an emergent property of the fluid. The same methods can also be used to simulate the curve-shortening flow, even when the curve undergoing the flow is not a boundary or shock. 1740:. On such a surface, the smooth compact set that has any given area and minimum perimeter for that area is necessarily a circle centered at the origin. The proof applies the curve-shortening flow to two curves, a metric circle and the boundary of any other compact set, and compares the change in perimeter of the two curves as they are both reduced to a point by the flow. The curve-shortening flow can also be used to prove the 1211:) bounded by two congruent arcs of circles together with two collinear rays having their apexes at the corners of the lens, and a "fish-shaped" network bounded by a line segment, two rays, and a convex curve. Any other self-similar shrinking networks involve a larger number of curves. Another family of networks grows homothetically and remains self-similar; these are tree-like networks of curves, meeting at angles of 2 1697: 1446:

parameterizations of the curve-shortening flow may allow the vertices that approximate the curve to move non-perpendicularly. In effect, this allows the vertices to move along the curve, as the curve evolves. Choosing a careful reparameterization can help redistribute the vertices more evenly along the curve in situations where perpendicular motion would cause them to bunch up.

96:. If two disjoint simple smooth closed curves evolve, they remain disjoint until one of them collapses to a point. The circle is the only simple closed curve that maintains its shape under the curve-shortening flow, but some curves that cross themselves or have infinite length keep their shape, including the grim reaper curve, an infinite curve that translates upwards, and 1639:, the grain boundaries in annealing are subject only to local effects, which cause them to move according to the mean curvature flow. The one-dimensional case of this flow, the curve-shortening flow, corresponds to annealing sheets of metal that are thin enough for the grains to become effectively two-dimensional and their boundaries to become one-dimensional. 1470:, and it can be used to help prove the existence of generalized flows as well as in their numerical simulation. Using it, the method of Crandall and Lions can be proven to converge and is the only numerical method listed by Cao that is equipped with bounds on its convergence rate. For an empirical comparison of the 1688:, the limiting behavior for fast reaction, slow diffusion, and two or more local minima of energy with the same energy level as each other is for the system to settle into regions of different local minima, with the fronts delimiting boundaries between these regions evolving according to the curve-shortening flow. 723:

conservation law. However, by combining the constant rate of area loss with the avoidance principle, it is possible to prove that the vanishing point always lies within a circle, concentric with the minimum enclosing circle, whose area is the difference in areas between the enclosing circle and the given curve.

971:. The proof comes from the observation that curve shortening preserves the smoothness and area-bisection properties of the curve, and does not increase its number of inflection points. Therefore, it allows the problem to be reduced to the problem for curves near the limiting shape of curve shortening, a 1780:

of its normal vectors, and form the gradient flow of this energy, according to which the normal speed at which the curve flows is proportional to an anisotropic analog of the curvature. This flow can be simulated by discretizing the curve as a polygon. In numerical experiments, initial curves appear

1223:

that meet at a common endpoint. The two-ray case of these shapes is an unbounded smooth curve; for three or more rays the evolution of these shapes may be defined using generalized variants of the curve-shortening flow such as the one for varifolds. A given fan of four or more rays may be asymptotic

1406:

The Angenent oval and shrinking circle solutions are the only ancient solutions whose timeslices bound bounded convex sets. The Grim Reaper, stationary halfspace and stationary strip solutions are the only examples whose timeslices bound unbounded convex sets. There exist many further (nonembedded)

1601:

to each pixel. It is possible to use kernels other than the heat kernel, or to adaptively refine the grid so that it has high resolution near the curve but does not waste time and memory on pixels far from the curve that do not contribute to the outcome. Instead of using only the two values in the

915:

When a locally convex self-crossing curve approaches a singularity as one of its loops shrinks, it either shrinks in a self-similar way or asymptotically approaches the grim reaper curve (described below) as it shrinks. When a loop collapses to a singularity, the amount of total absolute curvature

805:

New inflection points cannot be created by the curve-shortening flow. Each of the angles in the representation of the total absolute curvature as a sum decreases monotonically, except at the instants when two consecutive inflection points reach the same angle or position as each other and are both

1589:

The method can be generalized to the evolution of networks of curves, meeting at junctions and dividing the plane into more than three regions, by applying the same method simultaneously to each region. Instead of blurring and thresholding, this method can alternatively be described as applying a

470:

undergo the curve-shortening flow simultaneously, they remain disjoint as the flow progresses. The reason is that, if two smooth curves move in a way that creates a crossing, then at the time of first crossing the curves would necessarily be tangent to each other, without crossing. But, in such a

1018:

Because every other simple closed curve converges to a circle, the circle is the only simple closed curve that keeps its shape under the curve-shortening flow. However, there are many other examples of curves that are either non-simple (they include self-crossings) or non-closed (they extend to

1570:

In order for this scheme to be accurate, the time step must be large enough to cause the curve to move by at least one pixel even at points of low curvature, but small enough to cause the radius of blurring to be less than the minimum radius of curvature. Therefore, the size of a pixel must be

1445:

is used to derive formulas for the approximate normal vector and curvature at each vertex of the polygon, and these values are used to determine how to move each vertex in each time step. Although the curve-shortening flow is defined by the motion of a curve perpendicularly to itself, some

932:

On a Riemannian manifold, any smooth simple closed curve will remain smooth and simple as it evolves, just as in the Euclidean case. It will either collapse to a point in a finite amount of time, or remain smooth and simple forever. In the latter case, the curve necessarily converges to a

912:) has unequal areas in its two lobes, then eventually the smaller lobe will collapse to a point. However, if the two lobes have equal areas, then they will remain equal throughout the evolution of the curve, and the isoperimetric ratio will diverge as the curve collapses to a singularity. 722:

satisfied by the curve-shortening flow. This implies that it is not possible to express the "vanishing point" where the curve eventually collapses as an integral over the curve of any function of its points and their derivatives, because such an expression would lead to a forbidden second

1237:

to a flow problem is a curve whose evolution can be extrapolated backwards for all time, without singularities. All of the self-similar solutions that shrink or stay the same size rather than growing are ancient solutions in this sense; they can be extrapolated backwards by reversing the

471:

situation, the two curves' curvatures at the point of tangency would necessarily pull them apart rather than pushing them together into a crossing. For the same reason, a single simple closed curve can never evolve to cross itself. This phenomenon is known as the avoidance principle.

1668:

Gage–Hamilton–Grayson theorem) and the lifetime of a pair of points corresponds to the salience of a feature of the shape. Because of the resampled convolution method that they describe for computing a numerical approximation of the curve-shortening flow, they call their method the

1667:

of the curve as they progress through the flow, and drawing a graph that plots the positions of the inflection points around the curve against the time parameter. The inflection points will typically be removed from the curve in pairs as the curve becomes convex (according to the

945: 1450:

write that these methods are fast and accurate but that it is much more complicated to extend them to versions of the curve-shortening flow that apply to more complicated inputs than simple closed curves, where it is necessary to deal with singularities and changes of topology.

715:) a circle has the greatest possible area among simple closed curves of a given length, it follows that circles are the slowest curves to collapse to a point under the curve-shortening flow. All other curves take less time to collapse than a circle of the same length. 313:

Because the ingredients of this equation, the arc length, curvature, and time, are all unaffected by translations and rotations of the Euclidean plane, it follows that the flow defined by this equation is invariant under translations and rotations (or more precisely,

5912:

Schnürer, Oliver C.; Azouani, Abderrahim; Georgi, Marc; Hell, Juliette; Jangle, Nihar; Koeller, Amos; Marxen, Tobias; Ritthaler, Sandra; Sáez, Mariel; Schulze, Felix; Smith, Brian (2011), "Evolution of convex lens-shaped networks under the curve shortening flow",

604:

is arc length along the curve. The integrand is always non-negative, and for any smooth closed curve there exist arcs within which it is strictly positive, so the length decreases monotonically. More generally, for any evolution of curves whose normal speed is

710:

units of area per unit of time, independent of the curve. Therefore, the total time for a curve to shrink to a point is proportional to its area, regardless of its initial shape. Because the area of a curve is reduced at a constant rate, and (by the

1772:

materials, it is important to have variants of the curve-shortening flow for which the speed of flow depends on the orientation of a curve as well as on its curvature. One way of doing this is to define the energy of a curve to be the integral of a

291: 940:

Immersed curves on Riemannian manifolds, with finitely many self-crossings, become self-tangent only at a discrete set of times, at each of which they lose a crossing. As a consequence the number of self-crossing points is non-increasing.

1961:(the gradient flow for an energy functional combining the mean curvature and Gaussian curvature). The curve-shortening flow is a special case of the mean curvature flow and of the Gauss curvature flow for one-dimensional curves. 453:) the flow is well-defined for the short term. However, it may eventually reach a singular state with four or more curves meeting at a junction, and there may be more than one way to continue the flow past such a singularity. 436:

A commonly studied variation of the problem involves networks of interior-disjoint smooth curves, with junctions where three or more of the curves meet. When the junctions all have exactly three curves meeting at angles of

1323: 1515:

of the locations of nearby points along the curve, with Gaussian weights. The standard deviation of the Gaussian should be chosen to be small enough that, after this step, the sample points still have nearly-uniform

478:

is surrounded by a circle, both will remain disjoint for as long as they both exist. But the enclosing circle shrinks under the curvature flow, remaining circular, until it collapses, and by the avoidance principle

1905:

under which the curve-shortening flow is invariant. Under this flow, an analogue of the Gage–Hamilton–Grayson theorem applies, under which any simple closed curve eventually becomes convex and then converges to an

1921:

of the curve. A closely related curve evolution which moves straight segments of a polygonal curve at equal speeds but allows concave corners to move more quickly than unit speed instead forms a different type of

487:

were to never reach a singularity, it would be trapped at a single point at the time when the circle collapses, which is impossible for a smooth curve. This can be quantified by observing that the radius of the

83:

move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its

1708:, each cell in an infinite grid of cells may have one of a finite set of states, and all cells update their states simultaneously based only on the configuration of a small set of neighboring cells. A 405:. The normal vector in this case can be defined (as in the plane) as the derivative of the tangent vector with respect to arc length, normalized to be a unit vector; it is one of the components of the 591: 505:. He shows that the stretch factor is strictly decreasing at each of its local maxima, except for the case of the two ends of a diameter of a circle in which case the stretch factor is constant at 501:

quantifies the avoidance principle for a single curve in terms of the ratio between the arc length (of the shorter of two arcs) and Euclidean distance between pairs of points, sometimes called the

330:, and remains so until reaching a singularity at which the curvature blows up. For a smooth curve without crossings, the only possible singularity happens when the curve collapses to a point, but 1027:

stays unchanged by the curve-shortening flow. Lines are the only curves that are unaffected by the curve-shortening flow, although there exist more complex stable networks of curves, such as the

672: 1144: 1979:

so that they stay polygonal, with applications including pattern formation and synchronization in distributed systems of robots. Length-preserving polygonal flows can be used to solve the

1520:

As they show, this method converges to the curve-shortening distribution in the limit as the number of sample points grows and the normalized arc length of the convolution radius shrinks.

36:

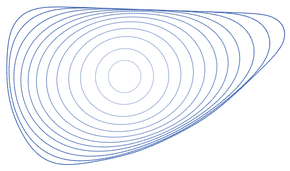
Convergence of a convex curve to a circle under the curve-shortening flow. Inner curves (lighter color) are flowed versions of the outer curves. Time steps between curves are not uniform.

1663:

that provides a simplified description of the shape at different levels of resolution. The method of Mokhtarian and Mackworth involves computing the curve-shortening flow, tracking the

1602:

pixelated image, a version of this method that uses an image whose pixel values represent the signed distance to the curve can achieve subpixel accuracy and require lower resolution.

2859:, "5.2.4 Bence, Merriman and Osher scheme for mean curvature motion", pp. 109–110. For the correctness of median filtering with other isotropic kernels, see section 4.4.1, pp. 90–92. 1394: 789: 334:

can have other types of singularity. In such cases, with some care it is possible to continue the flow past these singularities until the whole curve shrinks to a single point.

1242:

transformation that they would undergo by the forwards curve-shortening flow. Thus, for instance, the circle, grim reaper, and Abresch–Langer curves are all ancient solutions.

5656: 5594: 3257: 1893:. In this flow, the normal speed of the curve is proportional to the cube root of the curvature. The resulting flow is invariant (with a corresponding time scaling) under the 1882: 1972:, a modified version of the curve-shortening flow with additional forces has been used to find paths that strike a balance between being short and staying clear of obstacles. 1497:

suggest a numerical method for computing an approximation to the curve-shortening flow that maintains a discrete approximation to the curve and alternates between two steps:

1419:

In order to compute the curve-shortening flow efficiently, both a continuous curve and the continuous evolution of the curve need to be replaced by a discrete approximation.

1181: 509:. This monotonicity property implies the avoidance principle, for if the curve would ever touch itself the stretch factor would become infinite at the two touching points. 393:. The curve-shortening flow cannot cause a curve to depart from its convex hull, so this condition prevents parts of the curve from reaching the boundary of the manifold. 365:; examples such as this show that the reverse evolution of the curve-shortening flow can take well-behaved curves to complicated singularities in a finite amount of time. 326:

In order for the flow to be well defined, the given curve must be sufficiently smooth that it has a continuous curvature. However, once the flow starts, the curve becomes

1075: 210: 5095:

Huptych, Marcel; Röck, Sascha (28 January 2021), "Real-time path planning in dynamic environments for unmanned aerial vehicles using the curve-shortening flow method",

474:

The avoidance principle implies that any smooth closed curve must eventually reach a singularity, such as a point of infinite curvature. For, if a given smooth curve

1535:. The curve to be evolved is represented by assigning the value 0 (black) to pixels exterior to the curve, and 1 (white) to pixels interior to the curve, giving the 1467: 1712:

rule is one in which the grid is the infinite square lattice, there are exactly two cell states, the set of neighbors of each cell are the eight neighbors of the

1224:

to more than one different solution of this type, so these solutions do not provide a unique definition for the curve-shortening flow starting from a fan of rays.

17: 170:

into the Euclidean plane determined by the locations of each of its points. In the curve-shortening flow, each point of a curve moves in the direction of a

1659:

suggest applying the curve-shortening flow to the outline of a shape derived from a digital image, in order to remove noise from the shape and provide a

826:

as the whole curve shrinks to a single point. This behavior is sometimes summarized by saying that every simple closed curve shrinks to a "round point".

818:

If a smooth simple closed curve undergoes the curve-shortening flow, it remains smoothly embedded without self-intersections. It will eventually become

822:, and once it does so it will remain convex. After this time, all points of the curve will move inwards, and the shape of the curve will converge to a 373:

The curve-shortening flow, and many of the results about the curve-shortening flow, can be generalized from the Euclidean plane to any two-dimensional

5915: 4856: 4481:

Elliott, Charles M.; Fritz, Hans (2017), "On approximations of the curve shortening flow and of the mean curvature flow based on the DeTurck trick",

963:. This theorem states that every smooth simple closed curve on the sphere that divides the sphere's surface into two equal areas (like the seam of a 1458:

warns that "The conditions of stability cannot be determined easily and the time step must be chosen ad hoc." Another finite differencing method by

6034:

Vichniac, Gérard Y. (1986), "Cellular automata models of disorder and organization", in Bienenstock, E.; Fogelman Soulié, F.; Weisbuch, G. (eds.),

1427: 318:). If the plane is scaled by a constant dilation factor, the flow remains essentially unchanged, but is slowed down or sped up by the same factor. 1933:

For surfaces in higher dimensions, there is more than one definition of curvature, including extrinsic (embedding-dependent) measures such as the

1259: 4007:

Scale Space and PDE Methods in Computer Vision: 5th International Conference, Scale-Space 2005, Hofgeismar, Germany, April 7–9, 2005, Proceedings

1246: 158:

is a process in which the points of a space continuously change their locations or properties over time. More specifically, in a one-dimensional

4525: 4269:

Crandall, Michael G.; Lions, Pierre-Louis (1996), "Convergent difference schemes for nonlinear parabolic equations and mean curvature motion",

3396:

Andrews, Ben; Bryan, Paul (2011), "Curvature bound for curve shortening flow via distance comparison and a direct proof of Grayson's theorem",

1328:

and have as their limiting shape under reverse evolution a pair of grim reaper curves approaching each other from opposite directions. In the

1192:, remain self-similar with more complicated motions including rotation or combinations of rotation, shrinking or expansion, and translation. 3589: 3349:

Alvarez, Luis; Guichard, Frédéric; Lions, Pierre-Louis; Morel, Jean-Michel (1993), "Axioms and fundamental equations of image processing",

5361: 3351: 5474:

Computational Crystal Growers Workshop: Proceedings of the Geometry Center Workshop held in Minneapolis, Minnesota, February 22–28, 1992

5718:

Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids: A Collection of Reprints of 14 Seminal Papers

1152:

which has positive periodic solutions (corresponding to curves with self-similar evolution) for any period that is strictly between

1059:

of the curve without changing its shape or orientation. The grim reaper is the only curve with this property. It is also called the

806:

eliminated. Therefore, the total absolute curvature can never increase as the curve evolves. For convex curves it is constant at 2

202: 5528:

Mikula, Karol; Ševčovič, Daniel (2001), "Evolution of plane curves driven by a nonlinear function of curvature and anisotropy",

3942:

Broadbridge, Philip; Vassiliou, Peter (2011), "The role of symmetry and separation in surface evolution and curve shortening",

3554: 872:

The limiting shape for all networks of two collinear rays and two curves connecting the endpoints of the two rays. The central

425:. However, these extended definitions may allow parts of curves to vanish instantaneously or fatten into sets of nonzero area. 4170:, Collection Aléa-Saclay: Monographs and Texts in Statistical Physics, Cambridge University Press, Cambridge, pp. 37–38, 1253:. This family of curves may be parameterized by specifying the curvature as a function of the tangent angle using the formula 349:

and piecewise-smooth curves) instantly evolve into smooth curves, after which they evolve as any smooth curve would. However,

6051: 5833: 5733: 5284: 4943: 4432: 4032: 530: 3537:, Progress in Nonlinear Differential Equations and their Applications, vol. 7, Boston, MA: Birkhäuser, pp. 21–38, 4368:

Deckelnick, Klaus (2000), "Error bounds for a difference scheme approximating viscosity solutions of mean curvature flow",

1434:

to model and track the motion of boundaries between different materials, of steep gradients in material properties such as

130:

of metal sheets. Later, it was applied in image analysis to give a multi-scale representation of shapes. It can also model

615: 5775:

Rhines, Frederick N.; Craig, Kenneth R.; DeHoff, Robert T. (1974), "Mechanism of steady-state grain growth in aluminum",

4085: 2002:

is based on curve shortening, and evolves curves based on a combination of their curvature and the features of an image.

4452: 4049:(1995), "Characteristic cohomology of differential systems. II. Conservation laws for a class of parabolic equations", 3678:

Au, Thomas Kwok-Keung (2010), "On the saddle point property of Abresch-Langer curves under the curve shortening flow",

1878:), the resulting flow can be shown to obey the avoidance principle and an analog of the Gage–Hamilton–Grayson theorem. 5481: 5254: 4251: 4183: 4148: 4113: 3883: 1562:

Set every pixel with numerical value less than 1/2 to 0, and every pixel with numerical value greater than 1/2 to 1,

990: 984: 1441:

In front tracking methods for curve shortening, the curve undergoing the evolution is discretized as a polygon. The

845:) proved convergence to a circle for convex curves that contract to a point. More specifically Gage showed that the 681:

between the given evolution and the curve-shortening flow. Thus, the curve-shortening flow can be described as the

432:

For networks of curves, extending the curve-shortening flow past a singularity may result in ambiguity or fattening.

5408:

Lukyanov, S.L; Vitchev, E.S; Zamolodchikov, A.B (2004), "Integrable model of boundary interaction: the paperclip",

5048: 4958: 4726: 4693: 4563: 4321: 4203: 3492: 3318: 3195: 3115: 1501:

Resample the current curve by placing new sample points at a uniform spacing, as measured by normalized arc length.

3744:"The approximation of planar curve evolutions by stable fully implicit finite element schemes that equidistribute" 4520: 3901:

Bourni, Theodora; Langford, Mat; Tinaglia, Giuseppe (2020), "Convex ancient solutions to curve shortening flow",

1563: 857:

proved that all smooth convex curves eventually contract to a point without forming any other singularities, and

495:

must decrease at a rate that is at least as fast as the decrease in radius of a circle undergoing the same flow.

6066: 4420: 1741: 5499:

Mikula, Karol; Ševčovič, Daniel (1999), "Solution of nonlinearly curvature driven evolution of plane curves",

417:

It is possible to extend the definition of the flow to more general inputs than curves, for instance by using

4042: 3564:, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 533, Dordrecht: Kluwer Acad. Publ., pp. 3–10, 3448:(1991a), "Parabolic equations for curves on surfaces. II. Intersections, blow-up and generalized solutions", 3316:

Altschuler, Steven J.; Grayson, Matthew A. (1992), "Shortening space curves and flow through singularities",

1681: 1342: 685:

for length, the flow that (locally) decreases the length of the curve as quickly as possible relative to the

131: 2018:

The phrase "geometric heat flow" has also been used for flows on other kinds of object than curves, such as

4903:

Haußer, Frank; Voigt, Axel (2006), "A numerical scheme for regularized anisotropic curve shortening flow",

4684: 4634: 4600: 1744:, that every smooth Riemannian manifold topologically equivalent to a sphere has three geodesics that form 1709: 1102: 830: 745: 103:

An approximation to the curve-shortening flow can be computed numerically, by approximating the curve as a

5460: 900:

Curves that have self-crossings may reach singularities before contracting to a point. For instance, if a

6103: 6061: 5359:

Lauer, Joseph (2013), "A new length estimate for curve shortening flow and low regularity initial data",

3527: 1980: 1329: 5995:; Francis, Bruce A. (2007), "Curve shortening and the rendezvous problem for mobile autonomous robots", 1945:. Correspondingly, there are several ways of defining geometric flows based on curvature, including the 5962:

Scriven, L.E. (1960), "Dynamics of a fluid interface Equation of motion for Newtonian surface fluids",

5682: 3870: 406: 358: 5570: 4809: 3233: 1627:, in which heat treatment causes the boundaries between grains of crystallized metal to shift. Unlike 802:

for convex curves and larger for non-convex curves, serving as a measure of non-convexity of a curve.

201:

parameterizes a time in the evolution of the curve, the curve-shortening flow can be described by the

4605: 4096: 4051: 3840: 3786:

Bellettini, Giovanni; Novaga, Matteo (2011), "Curvature evolution of nonconvex lens-shaped domains",

1975:

Inspired by the curve-shortening flow on smooth curves, researchers have studied methods for flowing

1479: 1159: 1071: 93: 5237: 5126:

Ilmanen, Tom (1994), "Elliptic regularization and partial regularity for motion by mean curvature",

3838:; Cao, Jianguo (1996), "A new isoperimetric comparison theorem for surfaces of variable curvature", 3168: 5542: 5476:, Selected Lectures in Mathematics, Providence, RI: American Mathematical Society, pp. 73–83, 4763: 4639: 4015: 1725: 1512: 1442: 1200: 794:

It can also be expressed as a sum of the angles between the normal vectors at consecutive pairs of

732: 712: 286:{\displaystyle {\frac {\partial C}{\partial t}}={\frac {\partial ^{2}C}{\partial s^{2}}}=\kappa n,} 108: 85: 115:

of polygon vertices and then resampling vertices on the resulting curve, or repeatedly applying a

6168: 4308: 3113:

Abresch, U.; Langer, J. (1986), "The normalized curve shortening flow and homothetic solutions",

1965: 1917:. Curves evolved in this way will in general develop sharp corners, the trace of which forms the 1685: 905: 489: 362: 331: 327: 1462:

modifies the formula for the curvature at each vertex by adding to it a small term based on the

5537: 5232: 5188:

Ishimura, Naoyuki (1995), "Curvature evolution of plane curves with prescribed opening angle",

4724:

Grayson, Matthew A. (1987), "The heat equation shrinks embedded plane curves to round points",

4091: 4084:; Iben, Hayley N.; O'Brien, James F. (2004), "An energy-driven approach to linkage unfolding", 4010: 3261: 3163: 1624: 1052: 127: 865:

provide a simpler proof of Grayson's result, based on the monotonicity of the stretch factor.

6146: 5813: 4817: 4403:, Pitman Res. Notes Math. Ser., vol. 326, Longman Sci. Tech., Harlow, pp. 100–108, 4271: 3450: 1902: 1894: 1556: 1475: 1095: 1048: 354: 3726: 3193:

Altschuler, Steven J. (1991), "Singularities of the curve shrinking flow for space curves",

2793: 1074:

but remain self-similar under the curve-shortening flow. These have come to be known as the

377:. In order to avoid additional types of singularity, it is important for the manifold to be 337:

For a simple closed curve, using an extension of the flow to non-smooth curves based on the

6133: 6121: 6087: 5971: 5946: 5868: 5784: 5743: 5691: 5627: 5559: 5520: 5491: 5427: 5392: 5348: 5325: 5294: 5211: 5176: 5149: 5079: 5035: 4991: 4926: 4887: 4846: 4792: 4772: 4749: 4716: 4668: 4648: 4626: 4592: 4572: 4546: 4512: 4473: 4442: 4408: 4391: 4352: 4292: 4261: 4226: 4193: 4158: 4072: 3981: 3961: 3934: 3893: 3861: 3819: 3770: 3709: 3663: 3622: 3569: 3542: 3515: 3479: 3429: 3380: 3360: 3341: 3300: 3280: 3218: 3185: 3138: 2360:, Lemma 5.5, p. 130; "6.1 The decrease in total absolute curvature", pp. 144–147. 1991: 1954: 1923: 1733: 885: 467: 5648: 5026: 4982: 4523:; Weinstein, M. I. (1987), "A stable manifold theorem for the curve shortening equation", 4316: 997:

is non-increasing. This result can be used to analyze the singularities of the evolution.

884:

Similar results can be extended from closed curves to unbounded curves satisfying a local

92:

of the curve decreases as the curve converges to a circular shape, before collapsing to a

8: 4854:

Halldórsson, Höskuldur P. (2012), "Self-similar solutions to the curve shortening flow",

4688: 4312: 3788: 3632:; You, Qian (2021), "Ancient solutions to curve shortening with finite total curvature", 3398: 3011:, "3.2.3 The affine invariant flow: the simplest affine invariant curve flow", pp. 42–46. 1946: 1914: 1745: 1056: 960: 853:

for a circle and larger for any other convex curve) decreases monotonically and quickly.

846: 834: 374: 143: 89: 80: 61: 6125: 5975: 5788: 5695: 5431: 5352: 5180: 4776: 4652: 4576: 4009:, Lecture Notes in Computer Science, vol. 3459, Springer-Verlag, pp. 456–467, 3965: 3364: 3284: 1559:

of the indicator function, with radius proportional to the square root of the time step.

1539:

for the interior of the curve. This representation is updated by alternating two steps:

111:

to calculate the motion of each polygon vertex. Alternative methods include computing a

6111: 6091: 6022: 6004: 5950: 5924: 5900: 5800: 5763: 5713: 5677: 5631: 5605: 5443: 5417: 5396: 5370: 5338: 5260: 5166: 5114: 5083: 5057: 4891: 4865: 4834: 4796: 4672: 4490: 4399:

Deckelnick, K.; Dziuk, G. (1995), "On the approximation of the curve shortening flow",

4356: 4330: 4296: 4119: 3985: 3951: 3910: 3823: 3797: 3774: 3713: 3687: 3667: 3641: 3467: 3433: 3407: 3384: 3304: 3270: 1999: 1782: 1729: 1713: 1705: 1616: 1536: 1531:

describe a scheme operating on a two-dimensional square grid – effectively an array of

1014:

The grim reaper curve and translated copies of it produced by the curve-shortening flow

390: 155: 135: 5567:

Minarčík, Jiří; Beneš, Michal (2020), "Long-term behavior of curve shortening flow in

5512: 3292: 6095: 6047: 5983: 5829: 5804: 5729: 5635: 5477: 5447: 5400: 5316: 5280: 5250: 5118: 5087: 4939: 4800: 4676: 4428: 4300: 4247: 4179: 4144: 4109: 4046: 4028: 3879: 3388: 3147: 2019: 1927: 1595: 1508: 1035: 868: 694:

of the flow. This property is the one that gives the curve-shortening flow its name.

171: 5954: 5938: 5904: 5767: 5468:, CAM Report 92-18, Department of Mathematics, University of California, Los Angeles 5439: 5264: 4895: 4879: 4360: 4319:(2010), "Classification of compact ancient solutions to the curve shortening flow", 3827: 3778: 3717: 3671: 3437: 6108:

Proceedings of the International Congress of Mathematicians, Vol. I (Beijing, 2002)

6075: 6039: 6014: 5992: 5979: 5934: 5892: 5880: 5876: 5856: 5821: 5792: 5755: 5721: 5699: 5665: 5615: 5547: 5508: 5435: 5380: 5311: 5242: 5224: 5197: 5135: 5104: 5067: 5046:; Sinestrari, Carlo (2015), "Convex ancient solutions of the mean curvature flow", 5021: 5011: 4977: 4967: 4912: 4875: 4826: 4780: 4735: 4702: 4656: 4614: 4580: 4534: 4500: 4461: 4377: 4340: 4280: 4239: 4212: 4171: 4136: 4123: 4101: 4060: 4020: 3989: 3969: 3920: 3849: 3807: 3758: 3697: 3651: 3608: 3598: 3584: 3580: 3501: 3459: 3417: 3368: 3327: 3308: 3288: 3204: 3173: 3124: 1938: 1875: 1664: 1648: 1463: 1234: 1216: 1091: 1028: 968: 795: 719: 422: 342: 338: 6026: 4618: 4064: 3853: 3603: 1789:

before shrinking to a point. Alternatively, one can let the curve flow with speed

6150: 6129: 6083: 5942: 5864: 5825: 5623: 5555: 5516: 5487: 5388: 5321: 5290: 5207: 5145: 5075: 5043: 5031: 4999: 4987: 4953: 4922: 4883: 4842: 4788: 4745: 4712: 4664: 4622: 4588: 4542: 4508: 4469: 4438: 4416: 4404: 4387: 4348: 4288: 4257: 4222: 4189: 4154: 4087:

Proceedings of the Twentieth Annual Symposium on Computational Geometry (SCG '04)

4068: 3977: 3930: 3889: 3878:, Mathematical Notes, vol. 20, Princeton University Press, Princeton, N.J., 3857: 3815: 3766: 3743: 3705: 3659: 3629: 3618: 3576: 3565: 3550: 3538: 3523: 3511: 3487: 3475: 3445: 3425: 3376: 3337: 3296: 3227: 3214: 3181: 3177: 3134: 1987: 1942: 1774: 1652: 1598: 1239: 1204: 1024: 934: 909: 873: 402: 315: 139: 52:

by moving its points perpendicularly to the curve at a speed proportional to the

49: 6043: 5725: 5649:"A theory of multiscale, curvature-based shape representation for planar curves" 3151: 1913:

Transforming a curve with equal normal speeds at all points has been called the

1511:

with small standard deviation, in effect replacing each point's location with a

401:

The curve-shortening flow has also been studied for curves in three-dimensional

5820:, Advanced Courses in Mathematics – CRM Barcelona, Birkhäuser, pp. 72–75, 5644: 5220: 3925: 3835: 3701: 3042: 1995: 1953:(an intrinsic flow on the metric of a space based on its Ricci curvature), the 1934: 1898: 1757: 1636: 1431: 1333: 1245:

There are also examples which are not self-similar. An explicit example is the

1220: 736: 502: 159: 57: 5551: 5384: 5202: 5158: 5016: 4917: 4584: 4465: 3535:

Nonlinear diffusion equations and their equilibrium states, 3 (Gregynog, 1989)

2620:. For the generalization to two or more rays and issues of non-uniqueness see 1949:(in which the normal speed of an embedded surface is its mean curvature), the 1195:

For networks of smooth curves, meeting in threes at junctions with angles of 2

162:

such as the curve-shortening flow, the points undergoing the flow belong to a

6162: 5844: 5456: 5246: 5109: 5071: 4972: 4740: 4707: 4603:(1983), "An isoperimetric inequality with applications to curve shortening", 4344: 4217: 4175: 3506: 3332: 3209: 3129: 1969: 1958: 1591: 1552: 1548: 1435: 1208: 889: 877: 682: 678: 428: 297: 120: 116: 6018: 4956:(1990), "Asymptotic behavior for singularities of the mean curvature flow", 4504: 4401:

Calculus of variations, applications and computations (Pont-à-Mousson, 1994)

3811: 3421: 3090: 3078: 1318:{\displaystyle k(\theta ,t)={\sqrt {\cos 2\theta -\operatorname {coth} 2t}}} 123:

whose black and white pixels represent the inside and outside of the curve.

5709: 4538: 4081: 3973: 3490:(1991b), "On the formation of singularities in the curve shortening flow", 2816:, "5.2.3 A monotone and convergent finite difference schemes", p. 109. 1632: 1471: 1090:. These curves are locally convex, and therefore can be described by their 972: 819: 442: 350: 45: 5302:

Kimura, M. (1994), "Accurate numerical scheme for the flow by curvature",

5227:; Yezzi, A. (1995), "Gradient flows and geometric active contour models", 4284: 4243: 4105: 32: 4938:, Applied Mathematical Sciences, vol. 152 (2nd ed.), Springer, 4555: 4201:

Chou, Kai-Seng; Zhu, Xi-Ping (1998), "Shortening complete plane curves",

4135:, Lecture Notes in Mathematics, vol. 1805, Berlin: Springer-Verlag, 3562:

Hamiltonian systems with three or more degrees of freedom (S'Agaró, 1995)

2636: 2634: 1918: 1660: 1544: 1504: 994: 964: 949: 450: 386: 382: 112: 5140: 4024: 3655: 1586:, small enough to allow a suitable intermediate time step to be chosen. 6079: 5896: 5796: 5759: 5619: 5422: 5272: 4838: 4784: 4660: 4002: 3998: 3471: 3372: 2477: 1950: 1769: 1737: 1411:

convex examples as well as many further (nonconvex) embedded examples.

1067: 901: 5703: 5669: 3762: 3613: 2631: 6116: 5708: 4450:

Dziuk, Gerhard (1999), "Discrete anisotropic curve shortening flow",

4382: 3727:"A higher order scheme for the curve shortening flow of plane curves" 3692: 2906: 2598: 2553:, "2. Invariant solutions for the curve-shortening flow", pp. 27–44; 1628: 1066:

A family of self-crossing closed curves, derived from projections of

1047:

moves upwards without changing its shape. In the same way, any curve

175: 167: 53: 5860: 4830: 3463: 1010: 361:

is an example that instantly becomes smooth, despite not even being

6009: 5610: 5343: 4495: 4166:

Chopard, Bastien; Droz, Michel (1998), "2.2.4 The annealing rule",

4140: 3915: 3646: 3230:; Wu, Lani F. (2013), "The zoo of solitons for curve shortening in 3145: 3048: 686: 418: 353:

with nonzero measure instead immediately evolve into a topological

88:

decreases monotonically, until it becomes convex. Once convex, the

5929: 5375: 5277:

Numerical Geometry of Images: Theory, Algorithms, and Applications

5171: 5062: 4870: 4335: 3956: 3802: 3412: 3275: 2999:, Chapter 6: A Class of Non-convex Anisotropic Flows, pp. 143–177. 2670: 2045: 861:

proved that every non-convex curve will eventually become convex.

461: 6038:, NATO ASI Series, vol. 20, Springer-Verlag, pp. 3–20, 2840: 2838: 2476:, Theorem 2.2.1, p. 73. This result was already stated as a 2323: 1976: 1907: 1765: 1760:

related to the curve-shortening flow include the following ones.

346: 104: 5680:(1956), "Two-dimensional motion of idealized grain boundaries", 5218: 4079: 3096: 3084: 2658: 178:. For an evolving curve represented by a two-parameter function 126:

The curve-shortening flow was originally studied as a model for

5847:(1989), "Fast reaction, slow diffusion, and curve shortening", 5229:

Proceedings of IEEE International Conference on Computer Vision

5002:(1998), "A distance comparison principle for evolving curves", 4758: 4427:, Princeton, NJ: Princeton University Press, pp. 138–144, 3066: 2894: 2200: 1189: 1094:. Suitably scaled versions of these support functions obey the 956: 823: 518: 146:, and as a model for the behavior of higher-dimensional flows. 97: 6106:(2002), "Evolution of curves and surfaces by mean curvature", 5657:

IEEE Transactions on Pattern Analysis and Machine Intelligence

3225: 2835: 2558: 1700:

The Anneal cellular automaton, 1600 steps after a random start

1055:

by the curve-shortening flow, shifted in the direction of the

944: 849:(the ratio of squared curve length to area, a number that is 4 6064:(1989), "Some recent developments in differential geometry", 4759:"The shape of a figure-eight under the curve shortening flow" 3587:(1998), "On the affine heat equation for non-convex curves", 2862: 2164: 2128: 1532: 163: 5407: 4556:"Diffusion generated motion using signed distance functions" 4076:. See in particular Example 1, pp. 542–544 and 601–604. 3030: 2573: 2034:, p.140: "a geometric flow an evolution of the geometry of 1696: 1399:

In the physics literature, the same shapes are known as the

993:, the convolution of an evolving curve with a time-reversed 5335:

The level-set flow of the topologist's sine curve is smooth

4691:(1986), "The heat equation shrinking convex plane curves", 3742:

Barrett, John W.; Garcke, Harald; Nürnberg, Robert (2011),

2299: 703: 446: 4307: 2640: 5911: 5842: 5716:; Podio-Guidugli, Paulo; Slemrod, Marshall, eds. (1999), 4637:(1984), "Curve shortening makes convex curves circular", 3903:

Calculus of Variations and Partial Differential Equations

3348: 2912: 2604: 2437: 2311: 2152: 1886: 4001:(2005), "On similarity-invariant fairness measures", in 3575: 3555:"Inflection points, extatic points and curve shortening" 3020: 895: 706:

enclosed by the curve shrinks, at the constant rate of 2

6145:, Ph.D. thesis, The University of Wisconsin – Madison, 3054: 2682: 1566:

the image back to its original values in new positions.

586:{\displaystyle {\frac {dL}{dt}}=-\int \kappa ^{2}\,ds,} 4554:

Esedoḡlu, Selim; Ruuth, Steven; Tsai, Richard (2010),

3900: 2780:, "5.1.1 Finite difference methods", pp. 107–108. 2740:, "5.1.1 Finite difference methods", pp. 107–108. 2676: 2569: 2567: 2140: 2062: 2060: 1732:

is a non-increasing function of the distance from the

1623:) motivates it as a model for the physical process of 810:

and for non-convex curves it decreases monotonically.

5573: 3996: 3741: 3236: 2761: 2487: 2447: 2329: 1345: 1262: 1162: 1105: 1005: 748: 618: 533: 341:, there are only two possibilities. Curves with zero 213: 100:

that rotate while remaining the same size and shape.

4415: 3941: 3751:

Numerical Methods for Partial Differential Equations

2962: 2918: 2664: 2646: 2499: 2419: 2401: 2381: 2289: 2287: 2224: 2212: 2051: 2031: 739:

of the curvature along the arc length of the curve,

667:{\displaystyle {\frac {dL}{dt}}=-\int f\kappa \,ds,} 517:

As a curve undergoes the curve-shortening flow, its

5990: 5642: 5163:

On short time existence for the planar network flow

5156: 3072: 2900: 2825: 2625: 2564: 2511: 2407: 2236: 2206: 2193:, "4.7.1 Brakke's varifold solution", p. 100. 2116: 2057: 1719: 1656: 1615:An early reference to the curve-shortening flow by 1494: 1199:/3, the self-similar shrinking solutions include a 5818:Mean Curvature Flow and Isoperimetric Inequalities 5588: 5454: 3251: 2844: 2729: 1724:The curve-shortening flow can be used to prove an 1528: 1447: 1388: 1317: 1175: 1138: 783: 666: 585: 285: 166:, and what changes is the shape of the curve, its 5916:Transactions of the American Mathematical Society 5774: 5097:International Journal of Advanced Robotic Systems 5042: 4857:Transactions of the American Mathematical Society 4553: 3724: 3634:Transactions of the American Mathematical Society 3315: 2884: 2868: 2588: 2586: 2577: 2284: 2170: 2098: 1483: 978: 908:with a single crossing, resembling a figure 8 or 197:parameterizes the arc length along the curve and 6160: 5875: 5811: 4519: 3785: 3036: 2956: 2546: 2473: 2441: 2134: 2104: 1890: 1087: 813: 718:The constant rate of area reduction is the only 138:. The curve-shortening flow can be used to find 6110:, Higher Ed. Press, Beijing, pp. 525–538, 5190:Bulletin of the Australian Mathematical Society 4936:Front Tracking for Hyperbolic Conservation Laws 4398: 4041: 3789:Journal für die Reine und Angewandte Mathematik 3399:Journal für die Reine und Angewandte Mathematik 2753: 2694: 2305: 1019:infinity) and keep their shape. In particular, 462:Avoidance principle, radius, and stretch factor 64:. Other names for the same process include the 56:. The curve-shortening flow is an example of a 6036:Disordered Systems and Biological Organization 5527: 5498: 4526:Communications on Pure and Applied Mathematics 4168:Cellular automata modeling of physical systems 4133:Geometric Curve Evolution and Image Processing 2757: 2733: 2583: 5566: 4933: 4268: 3872:The motion of a surface by its mean curvature 3226:Altschuler, Dylan J.; Altschuler, Steven J.; 3112: 2805: 2717: 2542: 2158: 1459: 1079: 357:with nonzero area and smooth boundaries. The 5462:Diffusion generated motion by mean curvature 5128:Memoirs of the American Mathematical Society 4934:Holden, Helge; Risebro, Nils Henrik (2015), 4683: 4480: 4090:, New York, NY, USA: ACM, pp. 134–143, 4005:; Sochen, Nir A.; Weickert, Joachim (eds.), 3834: 3590:Journal of the American Mathematical Society 3395: 2952: 2765: 2574:Lukyanov, Vitchev & Zamolodchikov (2004) 2481: 862: 854: 596:where the integral is taken over the curve, 174:to the curve, at a rate proportional to the 5094: 4902: 4853: 4165: 3725:Balažovjech, Martin; Mikula, Karol (2009), 3628: 3352:Archive for Rational Mechanics and Analysis 3060: 2984: 2940: 2688: 2554: 1414: 726: 441:/3 (the same conditions seen in an optimal 6143:Some Ancient Solutions of Curve Shortening 5812:Ritoré, Manuel; Sinestrari, Carlo (2010), 5746:(1993), "Lava lamps in the 21st century", 4367: 4238:, Boca Raton, FL: Chapman & Hall/CRC, 3192: 2809: 2641:Daskalopoulos, Hamilton & Sesum (2010) 2616:The two-ray case was already described by 2273:, Appendix B, Proposition 1, p. 230; 2146: 1082:, although they were mentioned earlier by 927: 6115: 6008: 5928: 5609: 5576: 5541: 5421: 5374: 5342: 5315: 5236: 5201: 5170: 5139: 5108: 5061: 5025: 5015: 4981: 4971: 4916: 4869: 4739: 4706: 4494: 4381: 4334: 4216: 4095: 4014: 3997:Brook, Alexander; Bruckstein, Alfred M.; 3955: 3924: 3914: 3801: 3691: 3645: 3612: 3602: 3505: 3486: 3444: 3411: 3331: 3274: 3239: 3208: 3167: 3150:; Alberts, David; Gärtner, Bernd (1995), 3128: 2913:Rubinstein, Sternberg & Keller (1989) 2534: 2532: 2530: 2528: 2526: 2493: 2453: 2094: 1610: 771: 735:of a smooth curve is the integral of the 654: 573: 524:decreases at a rate given by the formula 368: 60:, and is the one-dimensional case of the 6033: 5885:International Journal of Computer Vision 5883:(1993), "Affine invariant scale-space", 5742: 5332: 5187: 4807: 4756: 3549: 3522: 3021:Angenent, Sapiro & Tannenbaum (1998) 2968: 2936: 2924: 2652: 2505: 2465: 2425: 2122: 2078: 2066: 1824:are smooth functions of the orientation 1695: 1489: 1250: 1009: 943: 867: 483:must remain contained within it. So, if 427: 31: 27:Motion of a curve based on its curvature 5961: 5676: 5125: 4998: 4952: 4723: 4233: 4200: 3680:Communications in Analysis and Geometry 3152:"A novel type of skeleton for polygons" 2996: 2880: 2789: 2713: 2617: 2550: 2538: 2517: 2413: 2393: 2369: 2357: 2274: 2254: 2242: 1620: 1551:for a short time step. The result is a 1389:{\displaystyle \cosh y-e^{-t}\cos x=0.} 1083: 858: 498: 203:parabolic partial differential equation 14: 6161: 5997:IEEE Transactions on Automatic Control 5471: 5301: 5271: 3868: 2888: 2749: 2677:Bourni, Langford & Tinaglia (2020) 2621: 2523: 2376:, Theorems 2 and 3, pp. 527–528; 2353: 2317: 2270: 2182: 1188:Other curves, including some infinite 959:can be used as part of a proof of the 677:which can be interpreted as a negated 6102: 6060: 5843:Rubinstein, Jacob; Sternberg, Peter; 5598:SIAM Journal on Mathematical Analysis 5358: 4449: 4234:Chou, Kai-Seng; Zhu, Xi-Ping (2001), 3156:Journal of Universal Computer Science 2980: 2762:Barrett, Garcke & Nürnberg (2011) 2469: 2373: 2356:, Appendix B, Proposition 2, p. 230; 2330:Brook, Bruckstein & Kimmel (2005) 2293: 2278: 2258: 2230: 2218: 2194: 2186: 2110: 2082: 1874:(so that the flow is invariant under 1675: 1631:, which are forced by differences in 1139:{\displaystyle h''+h={\frac {1}{h}},} 896:Singularities of self-crossing curves 784:{\displaystyle K=\int |\kappa |\,ds.} 381:; this is defined to mean that every 4633: 4599: 1691: 1547:to simulate its evolution under the 1543:Convolve the pixelated image with a 1228: 842: 838: 321: 6140: 5849:SIAM Journal on Applied Mathematics 5720:, Springer-Verlag, pp. 70–74, 5530:SIAM Journal on Applied Mathematics 4425:Discrete and Computational Geometry 4130: 3073:Smith, Broucke & Francis (2007) 3024: 3008: 2856: 2829: 2813: 2777: 2737: 2700: 2626:Ilmanen, Neves & Schulze (2014) 2397: 2377: 2341: 2207:Ilmanen, Neves & Schulze (2014) 2190: 1937:and intrinsic measures such as the 1523: 1507:the locations of the points with a 1455: 24: 5333:Lam, Casey; Lauer, Joseph (2016), 4453:SIAM Journal on Numerical Analysis 3677: 2845:Merriman, Bence & Osher (1992) 2730:Merriman, Bence & Osher (1992) 2665:Broadbridge & Vassiliou (2011) 2592: 1555:of the image, or equivalently the 1529:Merriman, Bence & Osher (1992) 1448:Merriman, Bence & Osher (1992) 1086:and rediscovered independently by 1006:Curves with self-similar evolution 1000: 837:, and Matthew Grayson. Gage ( 609:, the rate of change in length is 255: 241: 225: 217: 25: 6180: 5362:Geometric and Functional Analysis 4483:IMA Journal of Numerical Analysis 2901:Mokhtarian & Mackworth (1992) 2885:Rhines, Craig & DeHoff (1974) 2869:Esedoḡlu, Ruuth & Tsai (2010) 2826:Mokhtarian & Mackworth (1992) 1897:of the Euclidean plane, a larger 1657:Mokhtarian & Mackworth (1992) 1642: 1495:Mokhtarian & Mackworth (1992) 1422: 916:that is lost is either at least 2 5589:{\displaystyle \mathbb {R} ^{3}} 5049:Journal of Differential Geometry 5004:The Asian Journal of Mathematics 4959:Journal of Differential Geometry 4727:Journal of Differential Geometry 4694:Journal of Differential Geometry 4564:Journal of Computational Physics 4423:(2011), "5.5 Curve Shortening", 4322:Journal of Differential Geometry 4204:Journal of Differential Geometry 3493:Journal of Differential Geometry 3319:Journal of Differential Geometry 3252:{\displaystyle \mathbb {R} ^{n}} 3196:Journal of Differential Geometry 3116:Journal of Differential Geometry 1751: 1720:Construction of closed geodesics 412: 5939:10.1090/S0002-9947-2010-04820-2 5455:Merriman, Barry; Bence, James; 5440:10.1016/j.nuclphysb.2004.02.010 4880:10.1090/S0002-9947-2012-05632-7 3014: 3002: 2990: 2974: 2946: 2930: 2874: 2850: 2819: 2799: 2783: 2771: 2743: 2723: 2706: 2610: 2578:Huisken & Sinestrari (2015) 2459: 2431: 2387: 2363: 2347: 2335: 2264: 2248: 2176: 2171:Altschuler & Grayson (1992) 2099:Altschuler & Grayson (1992) 1764:For simulating the behavior of 1670:resampled curvature scale space 1635:to become surfaces of constant 1605: 1484:Balažovjech & Mikula (2009) 1482:finite difference methods, see 1430:methods have long been used in 1203:surrounding two equal areas, a 1176:{\displaystyle \pi {\sqrt {2}}} 702:For a simple closed curve, the 396: 6067:The Mathematical Intelligencer 5027:11858/00-001M-0000-0013-5965-2 4983:11858/00-001M-0000-0013-5CFE-3 4370:Interfaces and Free Boundaries 3037:Sapiro & Tannenbaum (1993) 2957:Ritoré & Sinestrari (2010) 2624:, Appendix C, pp. 235–237 and 2547:Epstein & Weinstein (1987) 2474:Ritoré & Sinestrari (2010) 2442:Bellettini & Novaga (2011) 2402:Devadoss & O'Rourke (2011) 2382:Devadoss & O'Rourke (2011) 2135:Ritoré & Sinestrari (2010) 2088: 2072: 2052:Devadoss & O'Rourke (2011) 2032:Devadoss & O'Rourke (2011) 2025: 2012: 1891:Sapiro & Tannenbaum (1993) 1742:theorem of the three geodesics 1466:. This modification is called 1278: 1266: 1088:Epstein & Weinstein (1987) 991:Huisken's monotonicity formula 985:Huisken's monotonicity formula 979:Huisken's monotonicity formula 767: 759: 490:smallest circle that encloses 149: 13: 1: 5536:(5): 1473–1501 (electronic), 5513:10.1016/S0168-9274(98)00130-5 5501:Applied Numerical Mathematics 5219:Kichenassamy, S.; Kumar, A.; 4808:Grayson, Matthew A. (1989b), 4757:Grayson, Matthew A. (1989a), 4619:10.1215/S0012-7094-83-05052-4 4065:10.1215/S0012-7094-95-07824-7 3854:10.1215/S0012-7094-96-08515-4 3604:10.1090/S0894-0347-98-00262-8 3105: 2754:Deckelnick & Dziuk (1995) 2306:Bryant & Griffiths (1995) 1816:is the (usual) curvature and 814:Gage–Hamilton–Grayson theorem 44:is a process that modifies a 18:Gage–Hamilton–Grayson theorem 5984:10.1016/0009-2509(60)87003-0 5964:Chemical Engineering Science 5826:10.1007/978-3-0346-0213-6_13 5317:10.1016/0893-9659(94)90056-6 4810:"Shortening embedded curves" 4236:The Curve Shortening Problem 3178:10.1007/978-3-642-80350-5_65 2959:, Theorem 2.3.1, p. 75. 2758:Mikula & Ševčovič (2001) 2734:Mikula & Ševčovič (1999) 2380:, Theorem 3.26, p. 47; 1883:affine curve-shortening flow 1710:Life-like cellular automaton 79:As the points of any smooth 7: 6044:10.1007/978-3-642-82657-3_1 5814:"2.2 Curve shortening flow" 5726:10.1007/978-3-642-59938-5_3 5304:Applied Mathematics Letters 4905:Applied Mathematics Letters 3869:Brakke, Kenneth A. (1978), 3293:10.1088/0951-7715/26/5/1189 3027:, Theorem 3.28, p. 47. 2806:Crandall & Lions (1996) 2718:Holden & Risebro (2015) 2543:Abresch & Langer (1986) 2159:Minarčík & Beneš (2020) 1910:as it collapses to a point. 1460:Crandall & Lions (1996) 1332:, they may be given by the 1330:Cartesian coordinate system 1249:solution after the work of 1080:Abresch & Langer (1986) 456: 310:is the unit normal vector. 10: 6185: 5777:Metallurgical Transactions 5683:Journal of Applied Physics 3926:10.1007/s00526-020-01784-8 3702:10.4310/CAG.2010.v18.n1.a1 3097:Kichenassamy et al. (1995) 2953:Benjamini & Cao (1996) 2891:, Appendix A, pp. 224–228. 2766:Elliott & Fritz (2017) 2482:Gage & Hamilton (1986) 1903:similarity transformations 1885:was first investigated by 1682:reaction–diffusion systems 1063:in the physics literature. 982: 967:) must have at least four 863:Andrews & Bryan (2011) 855:Gage & Hamilton (1986) 132:reaction–diffusion systems 5552:10.1137/S0036139999359288 5385:10.1007/s00039-013-0248-1 5203:10.1017/S0004972700014714 5161:; Schulze, Felix (2014), 5017:10.4310/ajm.1998.v2.n1.a2 4918:10.1016/j.aml.2005.05.011 4606:Duke Mathematical Journal 4585:10.1016/j.jcp.2009.10.002 4466:10.1137/S0036142998337533 4052:Duke Mathematical Journal 3841:Duke Mathematical Journal 3061:Huptych & Röck (2021) 2985:Haußer & Voigt (2006) 2941:Chopard & Droz (1998) 2689:Angenent & You (2021) 2281:, Theorem 1, p. 527. 512: 66:Euclidean shortening flow 5472:Taylor, Jean E. (1992), 5247:10.1109/iccv.1995.466855 5110:10.1177/1729881420968687 4764:Inventiones Mathematicae 4640:Inventiones Mathematicae 4309:Daskalopoulos, Panagiota 4176:10.1017/CBO9780511549755 3085:Cantarella et al. (2004) 3049:Aichholzer et al. (1995) 2559:Altschuler et al. (2013) 2006: 1981:carpenter's rule problem 1926:of the given curve, its 1726:isoperimetric inequality 1443:finite difference method 1415:Numerical approximations 1219:to a fan of two or more 1215:/3 at triple junctions, 733:total absolute curvature 727:Total absolute curvature 713:isoperimetric inequality 109:finite difference method 86:total absolute curvature 6019:10.1109/tac.2007.899024 3812:10.1515/CRELLE.2011.041 3422:10.1515/CRELLE.2011.026 1966:real-time path planning 1468:elliptic regularization 1454:For most such methods, 928:On Riemannian manifolds 697: 466:If two disjoint smooth 359:topologist's sine curve 5590: 5072:10.4310/jdg/1442364652 4973:10.4310/jdg/1214444099 4741:10.4310/jdg/1214441371 4708:10.4310/jdg/1214439902 4539:10.1002/cpa.3160400106 4345:10.4310/jdg/1279114297 4218:10.4310/jdg/1214424967 4131:Cao, Frédéric (2003), 4080:Cantarella, Jason H.; 3974:10.3842/SIGMA.2011.052 3507:10.4310/jdg/1214446558 3333:10.4310/jdg/1214448076 3253: 3210:10.4310/jdg/1214447218 3130:10.4310/jdg/1214440025 2605:Schnürer et al. (2011) 2438:Schnürer et al. (2011) 2123:Lam & Lauer (2016) 1895:affine transformations 1701: 1617:William W. Mullins 1611:Annealing metal sheets 1390: 1319: 1177: 1140: 1051:to the grim reaper is 1015: 955:Curve shortening on a 952: 881: 829:This result is due to 785: 668: 600:is the curvature, and 587: 433: 369:Non-Euclidean surfaces 287: 134:, and the behavior of 37: 5744:Pickover, Clifford A. 5591: 4818:Annals of Mathematics 4505:10.1093/imanum/drw020 4285:10.1007/s002110050228 4272:Numerische Mathematik 4244:10.1201/9781420035704 4106:10.1145/997817.997840 4047:Griffiths, Phillip A. 3528:"Shrinking doughnuts" 3451:Annals of Mathematics 3254: 2997:Chou & Zhu (2001) 2551:Chou & Zhu (2001) 2414:Chou & Zhu (1998) 2394:Chou & Zhu (2001) 2370:Chou & Zhu (2001) 2358:Chou & Zhu (2001) 2275:Chou & Zhu (2001) 2255:Chou & Zhu (2001) 1887:Alvarez et al. (1993) 1699: 1557:Weierstrass transform 1490:Resampled convolution 1391: 1320: 1178: 1141: 1096:differential equation 1076:Abresch–Langer curves 1013: 947: 871: 786: 669: 588: 431: 419:rectifiable varifolds 306:is the curvature and 288: 42:curve-shortening flow 35: 5993:Broucke, Mireille E. 5571: 5470:. Also published in 5231:, pp. 810–815, 3234: 2828:, pp. 796–797; 1992:active contour model 1955:Gauss curvature flow 1924:topological skeleton 1746:simple closed curves 1478:, and more accurate 1343: 1260: 1160: 1103: 1078:, after the work of 746: 616: 531: 468:simple closed curves 211: 144:Riemannian manifolds 74:arc length evolution 40:In mathematics, the 6126:2002math.....12407W 5991:Smith, Stephen L.; 5976:1960ChEnS..12...98S 5789:1974MT......5..413R 5748:The Visual Computer 5714:Kinderlehrer, David 5696:1956JAP....27..900M 5432:2004NuPhB.683..423L 5353:2016arXiv160102442L 5279:, Springer-Verlag, 5181:2014arXiv1407.4756I 4777:1989InMat..96..177G 4653:1984InMat..76..357G 4577:2010JCoPh.229.1017E 4417:Devadoss, Satyan L. 4025:10.1007/11408031_39 3966:2011SIGMA...7..052B 3524:Angenent, Sigurd B. 3365:1993ArRMA.123..199A 3285:2013Nonli..26.1189A 3228:Angenent, Sigurd B. 3146:Aichholzer, Oswin; 2320:, pp. 182–183. 1947:mean curvature flow 1915:grassfire transform 1781:to converge to the 1728:for surfaces whose 1686:Allen–Cahn equation 961:tennis ball theorem 886:Lipschitz condition 876:has the shape of a 847:isoperimetric ratio 835:Richard S. Hamilton 445:or two-dimensional 407:Frenet–Serret frame 389:, as defined using 375:Riemannian manifold 90:isoperimetric ratio 81:simple closed curve 70:geometric heat flow 62:mean curvature flow 6141:You, Qian (2014), 6080:10.1007/BF03025885 5897:10.1007/bf01420591 5797:10.1007/bf02644109 5760:10.1007/bf01900906 5620:10.1137/19M1248522 5586: 4785:10.1007/BF01393973 4661:10.1007/BF01388602 3736:, pp. 165–175 3373:10.1007/BF00375127 3249: 3148:Aurenhammer, Franz 2555:Halldórsson (2012) 2020:differential forms 2000:image segmentation 1730:Gaussian curvature 1714:Moore neighborhood 1706:cellular automaton 1702: 1676:Reaction–diffusion 1537:indicator function 1386: 1315: 1173: 1136: 1016: 953: 882: 781: 664: 583: 434: 391:geodesic convexity 379:convex at infinity 283: 38: 6053:978-3-642-82659-7 5881:Tannenbaum, Allen 5877:Sapiro, Guillermo 5845:Keller, Joseph B. 5835:978-3-0346-0213-6 5735:978-3-642-59938-5 5704:10.1063/1.1722511 5670:10.1109/34.149591 5410:Nuclear Physics B 5286:978-0-387-21637-9 5141:10.1090/memo/0520 4945:978-3-662-47507-2 4864:(10): 5285–5309, 4821:, Second Series, 4434:978-0-691-14553-2 4313:Hamilton, Richard 4043:Bryant, Robert L. 4034:978-3-540-25547-5 3950:: Paper 052, 19, 3763:10.1002/num.20637 3656:10.1090/tran/8186 3585:Tannenbaum, Allen 3581:Sapiro, Guillermo 3454:, Second Series, 2832:, pp. 10–11. 2810:Deckelnick (2000) 2147:Altschuler (1991) 1928:straight skeleton 1692:Cellular automata 1665:inflection points 1509:Gaussian function 1313: 1229:Ancient solutions 1171: 1131: 1092:support functions 1036:grim reaper curve 969:inflection points 796:inflection points 637: 552: 363:locally connected 322:Non-smooth curves 269: 232: 136:cellular automata 16:(Redirected from 6176: 6153: 6136: 6119: 6098: 6056: 6029: 6012: 6003:(6): 1154–1159, 5986: 5957: 5932: 5923:(5): 2265–2294, 5907: 5871: 5838: 5807: 5770: 5738: 5706: 5672: 5653: 5645:Mackworth, A. K. 5643:Mokhtarian, F.; 5638: 5613: 5604:(2): 1221–1231, 5595: 5593: 5592: 5587: 5585: 5584: 5579: 5562: 5545: 5523: 5494: 5469: 5467: 5450: 5425: 5403: 5378: 5369:(6): 1934–1961, 5355: 5346: 5328: 5319: 5297: 5267: 5240: 5214: 5205: 5183: 5174: 5152: 5143: 5121: 5112: 5090: 5065: 5044:Huisken, Gerhard 5038: 5029: 5019: 5000:Huisken, Gerhard 4994: 4985: 4975: 4954:Huisken, Gerhard 4948: 4929: 4920: 4898: 4873: 4849: 4814: 4803: 4752: 4743: 4719: 4710: 4679: 4629: 4613:(4): 1225–1229, 4601:Gage, Michael E. 4595: 4571:(4): 1017–1042, 4560: 4549: 4515: 4498: 4476: 4460:(6): 1808–1830, 4445: 4421:O'Rourke, Joseph 4411: 4394: 4385: 4363: 4338: 4303: 4264: 4229: 4220: 4196: 4161: 4126: 4099: 4097:10.1.1.1001.9683 4082:Demaine, Erik D. 4075: 4037: 4018: 3992: 3959: 3937: 3928: 3918: 3896: 3877: 3864: 3830: 3805: 3781: 3748: 3737: 3731: 3720: 3695: 3674: 3649: 3630:Angenent, Sigurd 3625: 3616: 3606: 3577:Angenent, Sigurd 3572: 3559: 3545: 3532: 3518: 3509: 3488:Angenent, Sigurd 3482: 3446:Angenent, Sigurd 3440: 3415: 3406:(653): 179–187, 3391: 3344: 3335: 3311: 3278: 3269:(5): 1189–1226, 3258: 3256: 3255: 3250: 3248: 3247: 3242: 3221: 3212: 3188: 3171: 3141: 3132: 3100: 3094: 3088: 3082: 3076: 3070: 3064: 3058: 3052: 3046: 3040: 3034: 3028: 3018: 3012: 3006: 3000: 2994: 2988: 2978: 2972: 2966: 2960: 2950: 2944: 2934: 2928: 2922: 2916: 2910: 2904: 2898: 2892: 2878: 2872: 2866: 2860: 2854: 2848: 2842: 2833: 2823: 2817: 2803: 2797: 2787: 2781: 2775: 2769: 2747: 2741: 2727: 2721: 2710: 2704: 2698: 2692: 2686: 2680: 2674: 2668: 2662: 2656: 2650: 2644: 2638: 2629: 2614: 2608: 2602: 2596: 2590: 2581: 2571: 2562: 2536: 2521: 2515: 2509: 2503: 2497: 2494:Angenent (1991a) 2491: 2485: 2463: 2457: 2454:Angenent (1991b) 2451: 2445: 2435: 2429: 2423: 2417: 2411: 2405: 2396:, p. vii; 2391: 2385: 2372:, p. vii; 2367: 2361: 2351: 2345: 2339: 2333: 2327: 2321: 2315: 2309: 2303: 2297: 2291: 2282: 2277:, p. vii; 2268: 2262: 2257:, p. vii; 2252: 2246: 2240: 2234: 2228: 2222: 2216: 2210: 2204: 2198: 2180: 2174: 2168: 2162: 2156: 2150: 2144: 2138: 2132: 2126: 2120: 2114: 2108: 2102: 2095:Angenent (1991a) 2092: 2086: 2076: 2070: 2064: 2055: 2049: 2043: 2041: 2037: 2029: 2023: 2016: 1939:scalar curvature 1876:point reflection 1873: 1863: 1850: 1840: 1827: 1823: 1819: 1815: 1811: 1788: 1779: 1649:image processing 1585: 1524:Median filtering 1513:weighted average 1464:Laplace operator 1395: 1393: 1392: 1387: 1370: 1369: 1324: 1322: 1321: 1316: 1314: 1285: 1235:ancient solution 1214: 1198: 1182: 1180: 1179: 1174: 1172: 1167: 1155: 1145: 1143: 1142: 1137: 1132: 1124: 1113: 1046: 1029:hexagonal tiling 937:of the surface. 923: 919: 852: 809: 801: 790: 788: 787: 782: 770: 762: 720:conservation law 709: 691: 673: 671: 670: 665: 638: 636: 628: 620: 608: 603: 599: 592: 590: 589: 584: 572: 571: 553: 551: 543: 535: 523: 508: 493: 486: 482: 477: 440: 423:level-set method 343:Lebesgue measure 339:level-set method 309: 305: 292: 290: 289: 284: 270: 268: 267: 266: 253: 249: 248: 238: 233: 231: 223: 215: 200: 196: 192: 140:closed geodesics 21: 6184: 6183: 6179: 6178: 6177: 6175: 6174: 6173: 6159: 6158: 6157: 6054: 5861:10.1137/0149007 5836: 5736: 5707:. Reprinted in 5651: 5580: 5575: 5574: 5572: 5569: 5568: 5484: 5465: 5287: 5257: 5238:10.1.1.331.6675 4946: 4831:10.2307/1971486 4812: 4689:Hamilton, R. S. 4558: 4435: 4254: 4186: 4151: 4116: 4035: 3886: 3875: 3836:Benjamini, Itai 3746: 3729: 3557: 3530: 3464:10.2307/2944327 3243: 3238: 3237: 3235: 3232: 3231: 3169:10.1.1.135.9800 3162:(12): 752–761, 3108: 3103: 3095: 3091: 3083: 3079: 3071: 3067: 3059: 3055: 3047: 3043: 3035: 3031: 3019: 3015: 3007: 3003: 2995: 2991: 2979: 2975: 2969:Grayson (1989b) 2967: 2963: 2951: 2947: 2937:Vichniac (1986) 2935: 2931: 2925:Pickover (1993) 2923: 2919: 2911: 2907: 2899: 2895: 2879: 2875: 2867: 2863: 2855: 2851: 2843: 2836: 2824: 2820: 2804: 2800: 2788: 2784: 2776: 2772: 2748: 2744: 2728: 2724: 2711: 2707: 2699: 2695: 2687: 2683: 2675: 2671: 2663: 2659: 2653:Angenent (1992) 2651: 2647: 2639: 2632: 2615: 2611: 2603: 2599: 2591: 2584: 2572: 2565: 2537: 2524: 2516: 2512: 2506:Angenent (1999) 2504: 2500: 2492: 2488: 2472:, p. 528; 2466:Grayson (1989b) 2464: 2460: 2452: 2448: 2436: 2432: 2426:Ishimura (1995) 2424: 2420: 2412: 2408: 2392: 2388: 2368: 2364: 2352: 2348: 2340: 2336: 2328: 2324: 2316: 2312: 2304: 2300: 2292: 2285: 2269: 2265: 2253: 2249: 2241: 2237: 2229: 2225: 2217: 2213: 2205: 2201: 2181: 2177: 2169: 2165: 2157: 2153: 2145: 2141: 2133: 2129: 2121: 2117: 2109: 2105: 2093: 2089: 2079:Grayson (1989a) 2077: 2073: 2067:Grayson (1989a) 2065: 2058: 2050: 2046: 2039: 2035: 2030: 2026: 2017: 2013: 2009: 1988:computer vision 1943:Ricci curvature 1861: 1852: 1838: 1829: 1825: 1821: 1817: 1813: 1790: 1786: 1777: 1775:smooth function 1758:geometric flows 1754: 1722: 1694: 1684:modeled by the 1678: 1653:computer vision 1645: 1613: 1608: 1572: 1526: 1492: 1425: 1417: 1401:paperclip model 1362: 1358: 1344: 1341: 1340: 1284: 1261: 1258: 1257: 1251:Angenent (1992) 1240:self-similarity 1231: 1212: 1196: 1166: 1161: 1158: 1157: 1153: 1123: 1106: 1104: 1101: 1100: 1038: 1008: 1003: 1001:Specific curves 987: 981: 935:closed geodesic 930: 921: 917: 910:infinity symbol 898: 850: 816: 807: 799: 766: 758: 747: 744: 743: 729: 707: 700: 687: 629: 621: 619: 617: 614: 613: 606: 601: 597: 567: 563: 544: 536: 534: 532: 529: 528: 521: 515: 506: 491: 484: 480: 475: 464: 459: 438: 415: 403:Euclidean space 399: 371: 345:(including all 332:immersed curves 324: 307: 301: 262: 258: 254: 244: 240: 239: 237: 224: 216: 214: 212: 209: 208: 198: 194: 179: 152: 50:Euclidean plane 28: 23: 22: 15: 12: 11: 5: 6182: 6172: 6171: 6169:Geometric flow 6156: 6155: 6138: 6100: 6058: 6052: 6031: 5988: 5959: 5909: 5873: 5855:(1): 116–133, 5840: 5834: 5809: 5783:(2): 413–425, 5772: 5754:(3): 173–177, 5740: 5734: 5690:(8): 900–904, 5678:Mullins, W. W. 5674: 5664:(8): 789–805, 5640: 5583: 5578: 5564: 5543:10.1.1.32.1138 5525: 5507:(2): 191–207, 5496: 5482: 5459:(April 1992), 5457:Osher, Stanley 5452: 5423:hep-th/0312168 5416:(3): 423–454, 5405: 5356: 5330: 5299: 5285: 5269: 5255: 5225:Tannenbaum, A. 5216: 5196:(2): 287–296, 5185: 5157:Ilmanen, Tom; 5154: 5123: 5092: 5056:(2): 267–287, 5040: 5010:(1): 127–133, 4996: 4966:(1): 285–299, 4950: 4944: 4931: 4911:(8): 691–698, 4900: 4851: 4805: 4771:(1): 177–180, 4754: 4734:(2): 285–314, 4721: 4681: 4647:(2): 357–364, 4631: 4597: 4551: 4533:(1): 119–139, 4521:Epstein, C. L. 4517: 4489:(2): 543–603, 4478: 4447: 4433: 4413: 4396: 4383:10.4171/IFB/15 4376:(2): 117–142, 4365: 4329:(3): 455–464, 4305: 4266: 4252: 4231: 4211:(3): 471–504, 4198: 4184: 4163: 4149: 4141:10.1007/b10404 4128: 4114: 4077: 4059:(3): 531–676, 4039: 4033: 4016:10.1.1.67.1807 3994: 3939: 3898: 3884: 3866: 3848:(2): 359–396, 3832: 3796:(656): 17–46, 3783: 3739: 3734:Algoritmy 2009 3722: 3675: 3640:(2): 863–880, 3626: 3597:(3): 601–634, 3573: 3547: 3520: 3500:(3): 601–633, 3484: 3458:(1): 171–215, 3442: 3393: 3359:(3): 199–257, 3346: 3326:(2): 283–298, 3313: 3246: 3241: 3223: 3203:(2): 491–514, 3190: 3143: 3123:(2): 175–196, 3109: 3107: 3104: 3102: 3101: 3089: 3077: 3065: 3053: 3041: 3029: 3013: 3001: 2989: 2973: 2961: 2945: 2929: 2917: 2905: 2893: 2881:Mullins (1956) 2873: 2861: 2849: 2834: 2818: 2798: 2790:Ilmanen (1994) 2782: 2770: 2742: 2722: 2714:Scriven (1960) 2705: 2693: 2681: 2669: 2657: 2645: 2630: 2618:Mullins (1956) 2609: 2597: 2582: 2563: 2539:Mullins (1956) 2522: 2518:Huisken (1990) 2510: 2498: 2486: 2458: 2446: 2430: 2418: 2406: 2404:, p. 141. 2400:, p. 47; 2386: 2384:, p. 141. 2362: 2346: 2344:, p. 143. 2334: 2322: 2310: 2298: 2283: 2263: 2247: 2243:Huisken (1998) 2235: 2233:, p. 527. 2223: 2221:, p. 526. 2211: 2199: 2175: 2163: 2151: 2139: 2127: 2115: 2103: 2087: 2071: 2056: 2054:, p. 140. 2044: 2024: 2010: 2008: 2005: 2004: 2003: 1996:edge detection 1984: 1973: 1962: 1935:mean curvature 1931: 1911: 1899:symmetry group 1879: 1753: 1750: 1736:, such as the 1721: 1718: 1693: 1690: 1677: 1674: 1644: 1643:Shape analysis 1641: 1637:mean curvature 1612: 1609: 1607: 1604: 1568: 1567: 1560: 1525: 1522: 1518: 1517: 1502: 1491: 1488: 1480:Crank–Nicolson 1476:backward Euler 1436:weather fronts 1432:fluid dynamics 1428:Front tracking 1424: 1423:Front tracking 1421: 1416: 1413: 1397: 1396: 1385: 1382: 1379: 1376: 1373: 1368: 1365: 1361: 1357: 1354: 1351: 1348: 1334:implicit curve 1326: 1325: 1312: 1309: 1306: 1303: 1300: 1297: 1294: 1291: 1288: 1283: 1280: 1277: 1274: 1271: 1268: 1265: 1230: 1227: 1226: 1225: 1193: 1185: 1184: 1170: 1165: 1149: 1148: 1147: 1146: 1135: 1130: 1127: 1122: 1119: 1116: 1112: 1109: 1084:Mullins (1956) 1072:homothetically 1064: 1032: 1007: 1004: 1002: 999: 983:Main article: 980: 977: 929: 926: 906:immersed curve 897: 894: 859:Grayson (1987) 815: 812: 792: 791: 780: 777: 774: 769: 765: 761: 757: 754: 751: 737:absolute value 728: 725: 699: 696: 675: 674: 663: 660: 657: 653: 650: 647: 644: 641: 635: 632: 627: 624: 594: 593: 582: 579: 576: 570: 566: 562: 559: 556: 550: 547: 542: 539: 514: 511: 503:stretch factor 499:Huisken (1998) 463: 460: 458: 455: 414: 411: 398: 395: 385:has a compact 370: 367: 323: 320: 296:a form of the 294: 293: 282: 279: 276: 273: 265: 261: 257: 252: 247: 243: 236: 230: 227: 222: 219: 160:geometric flow 151: 148: 107:and using the 58:geometric flow 26: 9: 6: 4: 3: 2: 6181: 6170: 6167: 6166: 6164: 6152: 6148: 6144: 6139: 6135: 6131: 6127: 6123: 6118: 6113: 6109: 6105: 6101: 6097: 6093: 6089: 6085: 6081: 6077: 6073: 6069: 6068: 6063: 6059: 6055: 6049: 6045: 6041: 6037: 6032: 6028: 6024: 6020: 6016: 6011: 6006: 6002: 5998: 5994: 5989: 5985: 5981: 5977: 5973: 5970:(2): 98–108, 5969: 5965: 5960: 5956: 5952: 5948: 5944: 5940: 5936: 5931: 5926: 5922: 5918: 5917: 5910: 5906: 5902: 5898: 5894: 5890: 5886: 5882: 5878: 5874: 5870: 5866: 5862: 5858: 5854: 5850: 5846: 5841: 5837: 5831: 5827: 5823: 5819: 5815: 5810: 5806: 5802: 5798: 5794: 5790: 5786: 5782: 5778: 5773: 5769: 5765: 5761: 5757: 5753: 5749: 5745: 5741: 5737: 5731: 5727: 5723: 5719: 5715: 5711: 5710:Ball, John M. 5705: 5701: 5697: 5693: 5689: 5685: 5684: 5679: 5675: 5671: 5667: 5663: 5659: 5658: 5650: 5646: 5641: 5637: 5633: 5629: 5625: 5621: 5617: 5612: 5607: 5603: 5599: 5581: 5565: 5561: 5557: 5553: 5549: 5544: 5539: 5535: 5531: 5526: 5522: 5518: 5514: 5510: 5506: 5502: 5497: 5493: 5489: 5485: 5483:0-8218-8072-1 5479: 5475: 5464: 5463: 5458: 5453: 5449: 5445: 5441: 5437: 5433: 5429: 5424: 5419: 5415: 5411: 5406: 5402: 5398: 5394: 5390: 5386: 5382: 5377: 5372: 5368: 5364: 5363: 5357: 5354: 5350: 5345: 5340: 5336: 5331: 5327: 5323: 5318: 5313: 5309: 5305: 5300: 5296: 5292: 5288: 5282: 5278: 5274: 5270: 5266: 5262: 5258: 5256:0-8186-7042-8 5252: 5248: 5244: 5239: 5234: 5230: 5226: 5222: 5217: 5213: 5209: 5204: 5199: 5195: 5191: 5186: 5182: 5178: 5173: 5168: 5164: 5160: 5155: 5151: 5147: 5142: 5137: 5133: 5129: 5124: 5120: 5116: 5111: 5106: 5102: 5098: 5093: 5089: 5085: 5081: 5077: 5073: 5069: 5064: 5059: 5055: 5051: 5050: 5045: 5041: 5037: 5033: 5028: 5023: 5018: 5013: 5009: 5005: 5001: 4997: 4993: 4989: 4984: 4979: 4974: 4969: 4965: 4961: 4960: 4955: 4951: 4947: 4941: 4937: 4932: 4928: 4924: 4919: 4914: 4910: 4906: 4901: 4897: 4893: 4889: 4885: 4881: 4877: 4872: 4867: 4863: 4859: 4858: 4852: 4848: 4844: 4840: 4836: 4832: 4828: 4825:(1): 71–111, 4824: 4820: 4819: 4811: 4806: 4802: 4798: 4794: 4790: 4786: 4782: 4778: 4774: 4770: 4766: 4765: 4760: 4755: 4751: 4747: 4742: 4737: 4733: 4729: 4728: 4722: 4718: 4714: 4709: 4704: 4700: 4696: 4695: 4690: 4686: 4682: 4678: 4674: 4670: 4666: 4662: 4658: 4654: 4650: 4646: 4642: 4641: 4636: 4632: 4628: 4624: 4620: 4616: 4612: 4608: 4607: 4602: 4598: 4594: 4590: 4586: 4582: 4578: 4574: 4570: 4566: 4565: 4557: 4552: 4548: 4544: 4540: 4536: 4532: 4528: 4527: 4522: 4518: 4514: 4510: 4506: 4502: 4497: 4492: 4488: 4484: 4479: 4475: 4471: 4467: 4463: 4459: 4455: 4454: 4448: 4444: 4440: 4436: 4430: 4426: 4422: 4418: 4414: 4410: 4406: 4402: 4397: 4393: 4389: 4384: 4379: 4375: 4371: 4366: 4362: 4358: 4354: 4350: 4346: 4342: 4337: 4332: 4328: 4324: 4323: 4318: 4317:Sesum, Natasa 4314: 4310: 4306: 4302: 4298: 4294: 4290: 4286: 4282: 4278: 4274: 4273: 4267: 4263: 4259: 4255: 4253:1-58488-213-1 4249: 4245: 4241: 4237: 4232: 4228: 4224: 4219: 4214: 4210: 4206: 4205: 4199: 4195: 4191: 4187: 4185:0-521-46168-5 4181: 4177: 4173: 4169: 4164: 4160: 4156: 4152: 4150:3-540-00402-5 4146: 4142: 4138: 4134: 4129: 4125: 4121: 4117: 4115:1-58113-885-7 4111: 4107: 4103: 4098: 4093: 4089: 4088: 4083: 4078: 4074: 4070: 4066: 4062: 4058: 4054: 4053: 4048: 4044: 4040: 4036: 4030: 4026: 4022: 4017: 4012: 4008: 4004: 4000: 3995: 3991: 3987: 3983: 3979: 3975: 3971: 3967: 3963: 3958: 3953: 3949: 3945: 3940: 3936: 3932: 3927: 3922: 3917: 3912: 3908: 3904: 3899: 3895: 3891: 3887: 3885:0-691-08204-9 3881: 3874: 3873: 3867: 3863: 3859: 3855: 3851: 3847: 3843: 3842: 3837: 3833: 3829: 3825: 3821: 3817: 3813: 3809: 3804: 3799: 3795: 3791: 3790: 3784: 3780: 3776: 3772: 3768: 3764: 3760: 3756: 3752: 3745: 3740: 3735: 3728: 3723: 3719: 3715: 3711: 3707: 3703: 3699: 3694: 3689: 3685: 3681: 3676: 3673: 3669: 3665: 3661: 3657: 3653: 3648: 3643: 3639: 3635: 3631: 3627: 3624: 3620: 3615: 3610: 3605: 3600: 3596: 3592: 3591: 3586: 3582: 3578: 3574: 3571: 3567: 3563: 3556: 3552: 3548: 3544: 3540: 3536: 3529: 3525: 3521: 3517: 3513: 3508: 3503: 3499: 3495: 3494: 3489: 3485: 3481: 3477: 3473: 3469: 3465: 3461: 3457: 3453: 3452: 3447: 3443: 3439: 3435: 3431: 3427: 3423: 3419: 3414: 3409: 3405: 3401: 3400: 3394: 3390: 3386: 3382: 3378: 3374: 3370: 3366: 3362: 3358: 3354: 3353: 3347: 3343: 3339: 3334: 3329: 3325: 3321: 3320: 3314: 3310: 3306: 3302: 3298: 3294: 3290: 3286: 3282: 3277: 3272: 3268: 3264: 3263: 3244: 3229: 3224: 3220: 3216: 3211: 3206: 3202: 3198: 3197: 3191: 3187: 3183: 3179: 3175: 3170: 3165: 3161: 3157: 3153: 3149: 3144: 3140: 3136: 3131: 3126: 3122: 3118: 3117: 3111: 3110: 3098: 3093: 3086: 3081: 3074: 3069: 3062: 3057: 3050: 3045: 3038: 3033: 3026: 3022: 3017: 3010: 3005: 2998: 2993: 2986: 2982: 2977: 2970: 2965: 2958: 2954: 2949: 2942: 2938: 2933: 2926: 2921: 2914: 2909: 2902: 2897: 2890: 2889:Brakke (1978) 2886: 2882: 2877: 2870: 2865: 2858: 2853: 2846: 2841: 2839: 2831: 2827: 2822: 2815: 2811: 2807: 2802: 2795: 2791: 2786: 2779: 2774: 2767: 2763: 2759: 2755: 2751: 2750:Kimura (1994) 2746: 2739: 2735: 2731: 2726: 2719: 2715: 2709: 2702: 2697: 2690: 2685: 2678: 2673: 2666: 2661: 2654: 2649: 2642: 2637: 2635: 2627: 2623: 2622:Brakke (1978) 2619: 2613: 2606: 2601: 2594: 2589: 2587: 2579: 2575: 2570: 2568: 2560: 2556: 2552: 2548: 2544: 2540: 2535: 2533: 2531: 2529: 2527: 2519: 2514: 2507: 2502: 2495: 2490: 2483: 2479: 2475: 2471: 2467: 2462: 2455: 2450: 2443: 2439: 2434: 2427: 2422: 2415: 2410: 2403: 2399: 2395: 2390: 2383: 2379: 2375: 2371: 2366: 2359: 2355: 2354:Brakke (1978) 2350: 2343: 2338: 2331: 2326: 2319: 2318:Kimmel (2004) 2314: 2307: 2302: 2295: 2290: 2288: 2280: 2276: 2272: 2271:Brakke (1978) 2267: 2260: 2256: 2251: 2244: 2239: 2232: 2227: 2220: 2215: 2208: 2203: 2196: 2192: 2188: 2184: 2183:Brakke (1978) 2179: 2172: 2167: 2160: 2155: 2148: 2143: 2137:, p. 72. 2136: 2131: 2124: 2119: 2112: 2107: 2100: 2096: 2091: 2084: 2080: 2075: 2068: 2063: 2061: 2053: 2048: 2033: 2028: 2021: 2015: 2011: 2001: 1997: 1993: 1989: 1985: 1982: 1978: 1974: 1971: 1970:mobile robots 1967: 1963: 1960: 1959:Willmore flow 1956: 1952: 1948: 1944: 1940: 1936: 1932: 1929: 1925: 1920: 1916: 1912: 1909: 1904: 1900: 1896: 1892: 1888: 1884: 1880: 1877: 1871: 1867: 1859: 1855: 1848: 1844: 1836: 1832: 1809: 1805: 1801: 1797: 1793: 1784: 1776: 1771: 1767: 1763: 1762: 1761: 1759: 1752:Related flows 1749: 1747: 1743: 1739: 1735: 1731: 1727: 1717: 1715: 1711: 1707: 1698: 1689: 1687: 1683: 1673: 1671: 1666: 1662: 1658: 1654: 1650: 1640: 1638: 1634: 1630: 1626: 1622: 1618: 1603: 1600: 1597: 1593: 1592:median filter 1587: 1583: 1579: 1575: 1565: 1561: 1558: 1554: 1553:Gaussian blur 1550: 1549:heat equation 1546: 1542: 1541: 1540: 1538: 1534: 1530: 1521: 1514: 1510: 1506: 1503: 1500: 1499: 1498: 1496: 1487: 1485: 1481: 1477: 1473: 1472:forward Euler 1469: 1465: 1461: 1457: 1452: 1449: 1444: 1439: 1437: 1433: 1429: 1420: 1412: 1410: 1404: 1402: 1383: 1380: 1377: 1374: 1371: 1366: 1363: 1359: 1355: 1352: 1349: 1346: 1339: 1338: 1337: 1335: 1331: 1310: 1307: 1304: 1301: 1298: 1295: 1292: 1289: 1286: 1281: 1275: 1272: 1269: 1263: 1256: 1255: 1254: 1252: 1248: 1247:Angenent oval 1243: 1241: 1236: 1222: 1218: 1210: 1209:vesica piscis 1206: 1202: 1201:double bubble 1194: 1191: 1187: 1186: 1168: 1163: 1151: 1150: 1133: 1128: 1125: 1120: 1117: 1114: 1110: 1107: 1099: 1098: 1097: 1093: 1089: 1085: 1081: 1077: 1073: 1069: 1065: 1062: 1061:hairpin model 1058: 1057:symmetry axis 1054: 1050: 1045: 1041: 1037: 1033: 1031:of the plane. 1030: 1026: 1022: 1021: 1020: 1012: 998: 996: 992: 989:According to 986: 976: 974: 970: 966: 962: 958: 951: 946: 942: 938: 936: 925: 913: 911: 907: 903: 893: 891: 890:vesica piscis 887: 879: 878:vesica piscis 875: 870: 866: 864: 860: 856: 848: 844: 840: 836: 832: 827: 825: 821: 811: 803: 797: 778: 775: 772: 763: 755: 752: 749: 742: 741: 740: 738: 734: 724: 721: 716: 714: 705: 695: 693: 690: 684: 683:gradient flow 680: 679:inner product 661: 658: 655: 651: 648: 645: 642: 639: 633: 630: 625: 622: 612: 611: 610: 580: 577: 574: 568: 564: 560: 557: 554: 548: 545: 540: 537: 527: 526: 525: 520: 510: 504: 500: 496: 494: 472: 469: 454: 452: 448: 444: 430: 426: 424: 420: 413:Beyond curves 410: 408: 404: 394: 392: 388: 384: 380: 376: 366: 364: 360: 356: 352: 351:Osgood curves 348: 344: 340: 335: 333: 329: 319: 317: 311: 304: 299: 298:heat equation 280: 277: 274: 271: 263: 259: 250: 245: 234: 228: 220: 207: 206: 205: 204: 190: 186: 182: 177: 173: 172:normal vector 169: 165: 161: 157: 147: 145: 141: 137: 133: 129: 124: 122: 121:digital image 118: 117:median filter 114: 110: 106: 101: 99: 95: 91: 87: 82: 77: 75: 71: 67: 63: 59: 55: 51: 47: 43: 34: 30: 19: 6142: 6117:math/0212407 6107: 6104:White, Brian 6074:(4): 41–47, 6071: 6065: 6062:White, Brian 6035: 6000: 5996: 5967: 5963: 5920: 5914: 5891:(1): 25–44, 5888: 5884: 5852: 5848: 5817: 5780: 5776: 5751: 5747: 5717: 5687: 5681: 5661: 5655: 5601: 5597: 5533: 5529: 5504: 5500: 5473: 5461: 5413: 5409: 5366: 5360: 5334: 5310:(1): 69–73, 5307: 5303: 5276: 5228: 5193: 5189: 5162: 5159:Neves, André 5131: 5127: 5100: 5096: 5053: 5047: 5007: 5003: 4963: 4957: 4935: 4908: 4904: 4861: 4855: 4822: 4816: 4768: 4762: 4731: 4725: 4701:(1): 69–96, 4698: 4692: 4644: 4638: 4610: 4604: 4568: 4562: 4530: 4524: 4486: 4482: 4457: 4451: 4424: 4400: 4373: 4369: 4326: 4320: 4279:(1): 17–41, 4276: 4270: 4235: 4208: 4202: 4167: 4132: 4086: 4056: 4050: 4006: 3947: 3943: 3906: 3902: 3871: 3845: 3839: 3793: 3787: 3754: 3750: 3733: 3693:math/0102088 3683: 3679: 3637: 3633: 3594: 3588: 3561: 3551:Angenent, S. 3534: 3497: 3491: 3455: 3449: 3403: 3397: 3356: 3350: 3323: 3317: 3266: 3262:Nonlinearity 3260: 3200: 3194: 3159: 3155: 3120: 3114: 3092: 3080: 3068: 3056: 3044: 3032: 3016: 3004: 2992: 2981:Dziuk (1999) 2976: 2964: 2948: 2932: 2920: 2908: 2896: 2876: 2864: 2852: 2821: 2801: 2785: 2773: 2745: 2725: 2708: 2696: 2684: 2672: 2660: 2648: 2612: 2600: 2513: 2501: 2489: 2470:White (2002) 2461: 2449: 2433: 2421: 2409: 2389: 2374:White (2002) 2365: 2349: 2337: 2325: 2313: 2301: 2294:White (1989) 2279:White (2002) 2266: 2259:White (2002) 2250: 2238: 2231:White (2002) 2226: 2219:White (2002) 2214: 2202: 2195:Lauer (2013) 2187:White (1989) 2178: 2166: 2154: 2142: 2130: 2118: 2111:Lauer (2013) 2106: 2090: 2083:White (2002) 2074: 2047: 2027: 2014: 1869: 1865: 1857: 1853: 1846: 1842: 1834: 1830: 1807: 1803: 1799: 1795: 1791: 1755: 1723: 1703: 1679: 1669: 1646: 1633:air pressure 1614: 1606:Applications 1588: 1581: 1577: 1573: 1569: 1564:thresholding 1527: 1519: 1493: 1453: 1440: 1426: 1418: 1408: 1405: 1400: 1398: 1327: 1244: 1232: 1060: 1043: 1042:= − log cos 1039: 1017: 988: 973:great circle 954: 939: 931: 914: 904:(any smooth 899: 883: 831:Michael Gage 828: 817: 804: 793: 730: 717: 701: 688: 676: 595: 516: 497: 473: 465: 451:soap bubbles 443:Steiner tree 435: 416: 400: 397:Space curves 378: 372: 336: 325: 312: 302: 295: 188: 184: 180: 153: 125: 102: 78: 73: 69: 65: 46:smooth curve 41: 39: 29: 5273:Kimmel, Ron 4635:Gage, M. E. 4003:Kimmel, Ron 3999:Kimmel, Ron 3686:(1): 1–21, 2712:See, e.g., 1919:medial axis 1783:Wulff shape 1770:anisotropic 1661:scale space 1545:heat kernel 1068:torus knots 995:heat kernel 965:tennis ball 950:tennis ball 920:or exactly 387:convex hull 383:compact set 316:equivariant 150:Definitions 113:convolution 94:singularity 6151:1641120538 6010:cs/0605070 5611:2212.11907 5344:1601.02442 4496:1602.07143 3916:1903.02022 3909:(4): 133, 3647:1803.01399 3614:1853/32428 3106:References 3025:Cao (2003) 3009:Cao (2003) 2857:Cao (2003) 2830:Cao (2003) 2814:Cao (2003) 2778:Cao (2003) 2738:Cao (2003) 2701:You (2014) 2478:conjecture 2398:Cao (2003) 2378:Cao (2003) 2342:Cao (2003) 2191:Cao (2003) 2038:over time 1957:, and the 1951:Ricci flow 1738:paraboloid 1629:soap films 1456:Cao (2003) 1217:asymptotic 1053:translated 902:lemniscate 6096:122335761 5930:0711.1108 5805:136991523 5636:216464044 5538:CiteSeerX 5448:119124585 5401:119339054 5376:1102.5110 5233:CiteSeerX 5221:Olver, P. 5172:1407.4756 5119:232093372 5088:119129510 5063:1405.7509 4871:1007.1617 4801:120965191 4677:121981987 4336:0806.1757 4301:119792668 4092:CiteSeerX 4011:CiteSeerX 3957:1106.0092 3803:0906.0166 3413:0908.2682 3389:121702431 3276:1207.4051 3164:CiteSeerX 2794:p. 1 2593:Au (2010) 2261:, p. 526. 1901:than the 1768:or other 1625:annealing 1375:⁡ 1364:− 1356:− 1350:⁡ 1336:equation 1305:⁡ 1299:− 1296:θ 1290:⁡ 1270:θ 1164:π 1070:, shrink 798:. It is 2 764:κ 756:∫ 652:κ 646:∫ 643:− 565:κ 561:∫ 558:− 275:κ 256:∂ 242:∂ 226:∂ 218:∂ 176:curvature 168:embedding 128:annealing 54:curvature 6163:Category 6147:ProQuest 5955:16595310 5905:13163111 5768:29417478 5647:(1992), 5275:(2004), 5265:10355426 4896:54018685 4685:Gage, M. 4361:18747005 3828:14158286 3779:23031256 3757:: 1–30, 3718:16046863 3672:59366007 3553:(1999), 3526:(1992), 3438:16124939 1977:polygons 1766:crystals 1596:Gaussian 1516:spacing. 1505:Convolve 1111:″ 457:Behavior 347:polygons 328:analytic 300:, where 6134:1989203 6122:Bibcode 6088:1016106 5972:Bibcode 5947:2763716 5869:0978829 5785:Bibcode 5692:Bibcode 5628:4076813 5560:1824511 5521:1708959 5492:1224451 5428:Bibcode 5393:3132906 5349:Bibcode 5326:1349897 5295:2028182 5212:1348488 5177:Bibcode 5150:1196160 5134:(520), 5080:3399098 5036:1656553 4992:1030675 4927:2232241 4888:2931330 4847:0979601 4839:1971486 4793:0981740 4773:Bibcode 4750:0906392 4717:0840401 4669:0742856 4649:Bibcode 4627:0726325 4593:2576237 4573:Bibcode 4547:0865360 4513:3649420 4474:1712165 4443:2790764 4409:1419337 4392:1760409 4353:2669361 4293:1417861 4262:1888641 4227:1690737 4194:1669736 4159:1976551 4124:6694097 4073:1334205 3990:8998552 3982:2804584 3962:Bibcode 3935:4127403 3894:0485012 3862:1417620 3820:2818854 3771:2743598 3710:2660456 3664:4196380 3623:1491538 3570:1720878 3543:1167827 3516:1100205 3480:1087347 3472:2944327 3430:2794630 3381:1225209 3361:Bibcode 3342:1158337 3309:1959710 3301:3043378 3281:Bibcode 3219:1131441 3186:1392429 3139:0845704 1908:ellipse 1828:. When 1619: ( 1599:weights 1409:locally 1207:shape ( 1190:spirals 1049:similar 892:shape. 421:or the 355:annulus 105:polygon 98:spirals 48:in the 6149: 6132: 6094: 6086: 6050: 6027:574140 6025: 5953: 5945: 5903: 5867: 5832: 5803: 5766: 5732: 5634: 5626: 5558: 5540: 5519: 5490: 5480: 5446: 5399: 5391: 5324: 5293: 5283: 5263: 5253: 5235: 5210: 5148: 5117: 5086: 5078: 5034: 4990: 4942: 4925: 4894: 4886: 4845: 4837: 4799: 4791: 4748: 4715: 4675: 4667: 4625: 4591: 4545: 4511: 4472: 4441: 4431: 4407: 4390: 4359: 4351: 4299: 4291: 4260: 4250: 4225: 4192: 4182: 4157: 4147: 4122: 4112: 4094: 4071: 4031: 4013: 3988: 3980: 3933: 3892: 3882: 3860: 3826: 3818: 3777: 3769: 3716: 3708: 3670: 3662: 3621: 3568: 3541: 3514: 3478: 3470: 3436: 3428: 3387: 3379: 3340: 3307: 3299: 3217: 3184: 3166: 3137: 1990:, the 1812:where 1756:Other 1734:origin 1533:pixels 1023:Every 957:sphere 824:circle 820:convex 519:length 513:Length 193:where 72:, and 6112:arXiv 6092:S2CID 6023:S2CID 6005:arXiv 5951:S2CID 5925:arXiv 5901:S2CID 5801:S2CID 5764:S2CID 5652:(PDF) 5632:S2CID 5606:arXiv 5466:(PDF) 5444:S2CID 5418:arXiv 5397:S2CID 5371:arXiv 5339:arXiv 5261:S2CID 5167:arXiv 5115:S2CID 5103:(1), 5084:S2CID 5058:arXiv 4892:S2CID 4866:arXiv 4835:JSTOR 4813:(PDF) 4797:S2CID 4673:S2CID 4559:(PDF) 4491:arXiv 4357:S2CID 4331:arXiv 4297:S2CID 4120:S2CID 3986:S2CID 3952:arXiv 3944:SIGMA 3911:arXiv 3876:(PDF) 3824:S2CID 3798:arXiv 3775:S2CID 3747:(PDF) 3730:(PDF) 3714:S2CID 3688:arXiv 3668:S2CID 3642:arXiv 3558:(PDF) 3531:(PDF) 3468:JSTOR 3434:S2CID 3408:arXiv 3385:S2CID 3305:S2CID 3271:arXiv 2007:Notes 1864:) = − 1704:In a 1594:with 1580:/max 1576:(min 164:curve 119:to a 6048:ISBN 5830:ISBN 5730:ISBN 5478:ISBN 5281:ISBN 5251:ISBN 4940:ISBN 4429:ISBN 4248:ISBN 4180:ISBN 4145:ISBN 4110:ISBN 4029:ISBN 3880:ISBN 3794:2011 3404:2011 1998:and 1994:for 1968:for 1941:and 1889:and 1881:The 1851:and 1841:) = 1820:and 1785:for 1651:and 1621:1956 1347:cosh 1302:coth 1221:rays 1205:lens 1156:and 1034:The 1025:line 874:lens 843:1984 839:1983 731:The 704:area 698:Area 692:norm 447:foam 156:flow 6076:doi 6040:doi 6015:doi 5980:doi 5935:doi 5921:363 5893:doi 5857:doi 5822:doi 5793:doi 5756:doi 5722:doi 5700:doi 5666:doi 5616:doi 5596:", 5548:doi 5509:doi 5436:doi 5414:683 5381:doi 5312:doi 5243:doi 5198:doi 5136:doi 5132:108 5105:doi 5068:doi 5054:101 5022:hdl 5012:doi 4978:hdl 4968:doi 4913:doi 4876:doi 4862:364 4827:doi 4823:129 4781:doi 4736:doi 4703:doi 4657:doi 4615:doi 4581:doi 4569:229 4535:doi 4501:doi 4462:doi 4378:doi 4341:doi 4281:doi 4240:doi 4213:doi 4172:doi 4137:doi 4102:doi 4061:doi 4021:doi 3970:doi 3921:doi 3850:doi 3808:doi 3759:doi 3698:doi 3652:doi 3638:374 3609:hdl 3599:doi 3502:doi 3460:doi 3456:133 3418:doi 3369:doi 3357:123 3328:doi 3289:doi 3259:", 3205:doi 3174:doi 3125:doi 2480:by 1986:In 1964:In 1680:In 1647:In 1372:cos 1287:cos 1233:An 449:of 142:on 6165:: 6130:MR 6128:, 6120:, 6090:, 6084:MR 6082:, 6072:11 6070:, 6046:, 6021:, 6013:, 6001:52 5999:, 5978:, 5968:12 5966:, 5949:, 5943:MR 5941:, 5933:, 5919:, 5899:, 5889:11 5887:, 5879:; 5865:MR 5863:, 5853:49 5851:, 5828:, 5816:, 5799:, 5791:, 5779:, 5762:, 5752:10 5750:, 5728:, 5712:; 5698:, 5688:27 5686:, 5662:14 5660:, 5654:, 5630:, 5624:MR 5622:, 5614:, 5602:52 5600:, 5556:MR 5554:, 5546:, 5534:61 5532:, 5517:MR 5515:, 5505:31 5503:, 5488:MR 5486:, 5442:, 5434:, 5426:, 5412:, 5395:, 5389:MR 5387:, 5379:, 5367:23 5365:, 5347:, 5337:, 5322:MR 5320:, 5306:, 5291:MR 5289:, 5259:, 5249:, 5241:, 5223:; 5208:MR 5206:, 5194:52 5192:, 5175:, 5165:, 5146:MR 5144:, 5130:, 5113:, 5101:18 5099:, 5082:, 5076:MR 5074:, 5066:, 5052:, 5032:MR 5030:, 5020:, 5006:, 4988:MR 4986:, 4976:, 4964:31 4962:, 4923:MR 4921:, 4909:19 4907:, 4890:, 4884:MR 4882:, 4874:, 4860:, 4843:MR 4841:, 4833:, 4815:, 4795:, 4789:MR 4787:, 4779:, 4769:96 4767:, 4761:, 4746:MR 4744:, 4732:26 4730:, 4713:MR 4711:, 4699:23 4697:, 4687:; 4671:, 4665:MR 4663:, 4655:, 4645:76 4643:, 4623:MR 4621:, 4611:50 4609:, 4589:MR 4587:, 4579:, 4567:, 4561:, 4543:MR 4541:, 4531:40 4529:, 4509:MR 4507:, 4499:, 4487:37 4485:, 4470:MR 4468:, 4458:36 4456:, 4439:MR 4437:, 4419:; 4405:MR 4388:MR 4386:, 4372:, 4355:, 4349:MR 4347:, 4339:, 4327:84 4325:, 4315:; 4311:; 4295:, 4289:MR 4287:, 4277:75 4275:, 4258:MR 4256:, 4246:, 4223:MR 4221:, 4209:50 4207:, 4190:MR 4188:, 4178:, 4155:MR 4153:, 4143:, 4118:, 4108:, 4100:, 4069:MR 4067:, 4057:78 4055:, 4045:; 4027:, 4019:, 3984:, 3978:MR 3976:, 3968:, 3960:, 3946:, 3931:MR 3929:, 3919:, 3907:59 3905:, 3890:MR 3888:, 3858:MR 3856:, 3846:85 3844:, 3822:, 3816:MR 3814:, 3806:, 3792:, 3773:, 3767:MR 3765:, 3755:27 3753:, 3749:, 3732:, 3712:, 3706:MR 3704:, 3696:, 3684:18 3682:, 3666:, 3660:MR 3658:, 3650:, 3636:, 3619:MR 3617:, 3607:, 3595:11 3593:, 3583:; 3579:; 3566:MR 3560:, 3539:MR 3533:, 3512:MR 3510:, 3498:33 3496:, 3476:MR 3474:, 3466:, 3432:, 3426:MR 3424:, 3416:, 3402:, 3383:, 3377:MR 3375:, 3367:, 3355:, 3338:MR 3336:, 3324:35 3322:, 3303:, 3297:MR 3295:, 3287:, 3279:, 3267:26 3265:, 3215:MR 3213:, 3201:34 3199:, 3182:MR 3180:, 3172:, 3158:, 3154:, 3135:MR 3133:, 3121:23 3119:, 3023:; 2983:; 2955:; 2939:; 2887:; 2883:; 2837:^ 2812:; 2808:; 2792:, 2764:; 2760:; 2756:; 2752:; 2736:; 2732:; 2716:; 2633:^ 2585:^ 2576:; 2566:^ 2557:; 2549:; 2545:; 2541:; 2525:^ 2468:; 2440:; 2286:^ 2189:; 2185:; 2097:; 2081:; 2059:^ 2042:." 1860:+ 1837:+ 1802:+ 1748:. 1655:, 1486:. 1474:, 1403:. 1384:0. 975:. 948:A 924:. 841:, 833:, 154:A 76:. 68:, 6154:. 6137:. 6124:: 6114:: 6099:. 6078:: 6057:. 6042:: 6030:. 6017:: 6007:: 5987:. 5982:: 5974:: 5958:. 5937:: 5927:: 5908:. 5895:: 5872:. 5859:: 5839:. 5824:: 5808:. 5795:: 5787:: 5781:5 5771:. 5758:: 5739:. 5724:: 5702:: 5694:: 5673:. 5668:: 5639:. 5618:: 5608:: 5582:3 5577:R 5563:. 5550:: 5524:. 5511:: 5495:. 5451:. 5438:: 5430:: 5420:: 5404:. 5383:: 5373:: 5351:: 5341:: 5329:. 5314:: 5308:7 5298:. 5268:. 5245:: 5215:. 5200:: 5184:. 5179:: 5169:: 5153:. 5138:: 5122:. 5107:: 5091:. 5070:: 5060:: 5039:. 5024:: 5014:: 5008:2 4995:. 4980:: 4970:: 4949:. 4930:. 4915:: 4899:. 4878:: 4868:: 4850:. 4829:: 4804:. 4783:: 4775:: 4753:. 4738:: 4720:. 4705:: 4680:. 4659:: 4651:: 4630:. 4617:: 4596:. 4583:: 4575:: 4550:. 4537:: 4516:. 4503:: 4493:: 4477:. 4464:: 4446:. 4412:. 4395:. 4380:: 4374:2 4364:. 4343:: 4333:: 4304:. 4283:: 4265:. 4242:: 4230:. 4215:: 4197:. 4174:: 4162:. 4139:: 4127:. 4104:: 4063:: 4038:. 4023:: 3993:. 3972:: 3964:: 3954:: 3948:7 3938:. 3923:: 3913:: 3897:. 3865:. 3852:: 3831:. 3810:: 3800:: 3782:. 3761:: 3738:. 3721:. 3700:: 3690:: 3654:: 3644:: 3611:: 3601:: 3546:. 3519:. 3504:: 3483:. 3462:: 3441:. 3420:: 3410:: 3392:. 3371:: 3363:: 3345:. 3330:: 3312:. 3291:: 3283:: 3273:: 3245:n 3240:R 3222:. 3207:: 3189:. 3176:: 3160:1 3142:. 3127:: 3099:. 3087:. 3075:. 3063:. 3051:. 3039:. 2987:. 2971:. 2943:. 2927:. 2915:. 2903:. 2871:. 2847:. 2796:. 2768:. 2720:. 2703:. 2691:. 2679:. 2667:. 2655:. 2643:. 2628:. 2607:. 2595:. 2580:. 2561:. 2520:. 2508:. 2496:. 2484:. 2456:. 2444:. 2428:. 2416:. 2332:. 2308:. 2296:. 2245:. 2209:. 2197:. 2173:. 2161:. 2149:. 2125:. 2113:. 2101:. 2085:. 2069:. 2040:t 2036:C 2022:. 1983:. 1930:. 1872:) 1870:θ 1868:( 1866:b 1862:π 1858:θ 1856:( 1854:b 1849:) 1847:θ 1845:( 1843:a 1839:π 1835:θ 1833:( 1831:a 1826:θ 1822:b 1818:a 1814:κ 1810:) 1808:θ 1806:( 1804:b 1800:κ 1798:) 1796:θ 1794:( 1792:a 1787:γ 1778:γ 1584:) 1582:κ 1578:κ 1574:O 1381:= 1378:x 1367:t 1360:e 1353:y 1311:t 1308:2 1293:2 1282:= 1279:) 1276:t 1273:, 1267:( 1264:k 1213:π 1197:π 1183:. 1169:2 1154:π 1134:, 1129:h 1126:1 1121:= 1118:h 1115:+ 1108:h 1044:x 1040:y 922:π 918:π 880:. 851:π 808:π 800:π 779:. 776:s 773:d 768:| 760:| 753:= 750:K 708:π 689:L 662:, 659:s 656:d 649:f 640:= 634:t 631:d 626:L 623:d 607:f 602:s 598:κ 581:, 578:s 575:d 569:2 555:= 549:t 546:d 541:L 538:d 522:L 507:π 492:C 485:C 481:C 476:C 439:π 437:2 308:n 303:κ 281:, 278:n 272:= 264:2 260:s 251:C 246:2 235:= 229:t 221:C 199:t 195:s 191:) 189:t 187:, 185:s 183:( 181:C 20:)

Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.

Knowledge

Curve-shortening flow

Index