483:
760:
792:
744:
776:
808:
29:
302:
to the 10-regular
Clebsch graph. Two copies of the 5-regular Clebsch graph can be produced in the same way from a 5-dimensional hypercube, by connecting pairs of vertices whose Hamming distance is exactly four.
387:
553:
four-chromatic graph, and every four-chromatic induced subgraph of the
Clebsch graph is a supergraph of the Grötzsch graph. More strongly, every triangle-free four-chromatic graph with no
665:
209:; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician
431:
710:
675:
consists entirely of integers. The
Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
759:
248:(the 5-regular Clebsch graph) may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an
902:
579:
in the orientable manifold of genus 5, forming pentagonal faces; and in the non-orientable surface of genus 6, forming tetragonal faces.
286:
of the 5-regular graph. It may also be constructed from the vertices of a 5-dimensional hypercube, by connecting pairs of vertices whose
791:
807:
1101:
Randerath, Bert; Schiermeyer, Ingo; Tewes, Meike (2002), "Three-colourability and forbidden subgraphs. II. Polynomial algorithms",
775:
732:, meaning that every isomorphism between two connected induced subgraphs can be extended to an automorphism of the whole graph.
522:(3,3,3) describing the minimum number of vertices in a complete graph without a triangle-free three-coloring is at least 17.
177:
667:. Because this polynomial can be completely factored into linear terms with integer coefficients, the Clebsch graph is an
1004:
743:
271:
GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a
318:
1156:
557:
of length six or more is an induced subgraph of the
Clebsch graph and an induced supergraph of the Grötzsch graph.
1103:
538:
594:
541:
has five vertices, not enough to partition the graph into three independent color classes. It contains as an
504:
may be partitioned into three disjoint copies of the 5-regular
Clebsch graph. Because the Clebsch graph is a
389:. Its complement, the 10-regular Clebsch graph, is therefore also a strongly regular graph, with parameters
1146:
576:
725:
588:
283:
198:
169:
449:
909:
291:
1151:
713:
392:
161:
76:
66:
561:
453:
312:
267:
Another construction, leading to the same graph, is to create a vertex for each element of the
149:
877:(1868), "Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen",
294:. It produces two subsets of 16 vertices that are disconnected from each other; both of these
721:
672:
482:
261:
165:
46:
996:
1126:
1087:
963:
688:
86:
8:
712:. As a Cayley graph, its automorphism group acts transitively on its vertices, making it
550:
505:
205:
with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5
56:
96:
1117:
564:
of dimension two, part of a family of graphs used to find tilings of high-dimensional
766:
750:
729:
461:
437:
299:
279:
245:
214:
206:
153:
1037:
546:
1112:
1013:
949:
861:
782:
542:
457:
287:
106:
1122:
1083:
959:
840:
814:
798:
717:
565:
260:
edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by
126:
116:
937:
874:
668:
534:
495:
472:
465:
445:
272:
222:
210:
39:
1140:
1064:
683:
516:
230:
202:
992:
954:
679:
554:
476:
441:
268:
190:
157:
136:
508:, this shows that there is a triangle-free three-coloring of the edges of
295:
186:
1065:"An easy proof of the Greenwood–Gleason evaluation of the Ramsey number
290:
is exactly two. This construction is an instance of the construction of
978:
569:
28:
1017:
979:"Constructions and Characterizations of (Semi)partial Geometries"
460:
by the ten non-neighbors of any vertex in this graph forms an
682:
with an automorphism group of order 1920, isomorphic to the
264:
together (or contracting) every opposite pair of vertices.
1100:
940:(1955), "Combinatorial relations and chromatic graphs",
864:
having eigenvalue 3, Lin. Alg. Appl. 1 (1968) 281-298.
221:
after the work of Robert E. Greenwood and
691:
597:
395:
321:
860:
J. J. Seidel, Strongly regular graphs with (−1,1,0)
16:
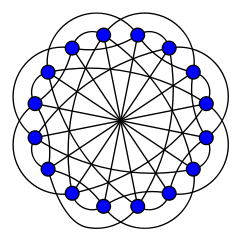
One of two different regular graphs with 16 vertices
526:used this construction as part of their proof that
903:"The Clebsch Graph on Bill Cherowitzo's home page"
704:
659:
425:
381:
575:The 5-regular Clebsch graph can be embedded as a
1138:
981:. Summer School on Finite Geometries. p. 6.
935:
523:
226:
879:Journal für die reine und angewandte Mathematik
252:-dimensional hypercube, a pair of vertices are
382:{\displaystyle (v,k,\lambda ,\mu )=(16,5,0,2)}
1053:. Master Thesis, University of Tübingen, 2018
537:with four colors, but not three: its largest
897:
895:
893:
834:
832:
1116:
976:
953:
890:
813:Construction of the Clebsch graph from a
213:. The 40-edge variant is the dimension-5
1062:
829:
660:{\displaystyle (x+3)^{5}(x-1)^{10}(x-5)}
481:
873:
843:. From MathWorld—A Wolfram Web Resource
582:
1139:
991:
282:(the 10-regular Clebsch graph) is the
256:if the shortest path between them has
997:"Problems in algebraic combinatorics"
985:
838:
931:
929:
1063:Sun, Hugo S.; Cohen, M. E. (1984),
1051:Engineering Linear Layouts with SAT
1005:Electronic Journal of Combinatorics
572:no two of which meet face-to-face.
560:The 5-regular Clebsch graph is the
533:The 5-regular Clebsch graph may be
490:3-coloured as three Clebsch graphs.
13:
591:of the 5-regular Clebsch graph is
14:
1168:
926:
678:The 5-regular Clebsch graph is a
311:The 5-regular Clebsch graph is a
806:
790:
774:
758:
742:
27:
1094:
1056:
942:Canadian Journal of Mathematics
801:of the Clebsch graph is 5.
785:of the Clebsch graph is 4.
769:of the Clebsch graph is 8.
436:The 5-regular Clebsch graph is
239:
229:), who used it to evaluate the
1043:
1030:
970:
867:
854:
654:
642:
633:
620:
611:
598:
524:Greenwood & Gleason (1955)
420:
396:
376:
352:
346:
322:
178:Table of graphs and parameters
1:
1118:10.1016/S0012-365X(01)00335-1
822:
306:
219:Greenwood–Gleason graph
315:of degree 5 with parameters
7:
426:{\displaystyle (16,10,6,6)}
201:graphs on 16 vertices, a 5-
10:
1173:
735:
217:; it is also known as the
1040:on DesignTheory.org, 2001
977:De Clerck, Frank (1997).
589:characteristic polynomial
176:
145:
135:
125:
115:
105:
95:
85:
75:
65:
55:
45:
35:
26:
21:
530:(3,3,3) = 17.
458:subgraph that is induced
236:(3,3,3) = 17.
1157:Strongly regular graphs
1076:The Fibonacci Quarterly
1038:Strongly regular graphs
955:10.4153/CJM-1955-001-4
706:
661:
491:
427:
383:
313:strongly regular graph
749:The Clebsch graph is
730:connected-homogeneous
707:
705:{\displaystyle D_{5}}
662:
485:
428:
384:
298:of the hypercube are
1104:Discrete Mathematics
689:
595:
583:Algebraic properties
515:; that is, that the
448:. It is also both 5-
393:
319:
839:Weisstein, Eric W.
726:distance transitive
506:triangle-free graph
170:Distance-transitive
936:Greenwood, R. E.;
716:. In fact, it is
702:
657:
492:
423:
379:
292:Frankl–Rödl graphs
1147:Individual graphs
1036:Peter J. Cameron
767:achromatic number
714:vertex transitive
494:The edges of the
280:halved cube graph
246:folded cube graph
223:Andrew M. Gleason
215:folded cube graph
207:halved cube graph
197:is either of two
183:
182:
162:Vertex-transitive
1164:
1131:
1129:
1120:
1111:(1–3): 137–153,
1098:
1092:
1090:
1073:
1060:
1054:
1047:
1041:
1034:
1028:
1027:
1025:
1024:
1001:
989:
983:
982:
974:
968:
966:
957:
933:
924:
923:
921:
920:
914:
908:. Archived from
907:
899:
888:
886:
871:
865:
862:adjacency matrix
858:
852:
851:
849:
848:
836:
810:
794:
783:chromatic number
778:
762:
746:
711:
709:
708:
703:
701:
700:
666:
664:
663:
658:
641:
640:
619:
618:
566:Euclidean spaces
543:induced subgraph
450:vertex-connected
432:
430:
429:
424:
388:
386:
385:
380:
288:Hamming distance
278:The dimension-5
244:The dimension-5
150:Strongly regular
107:Chromatic number
31:
19:
18:
1172:
1171:
1167:
1166:
1165:
1163:
1162:
1161:
1137:
1136:
1135:
1134:
1099:
1095:
1071:
1061:
1057:
1048:
1044:
1035:
1031:
1022:
1020:
999:
990:
986:
975:
971:
934:
927:
918:
916:
912:
905:
901:
900:
891:
872:
868:
859:
855:
846:
844:
841:"Clebsch Graph"
837:
830:
825:
818:
815:hypercube graph
811:
802:
799:chromatic index
795:
786:
779:
770:
763:
754:
747:
738:
722:edge transitive
696:
692:
690:
687:
686:
636:
632:
614:
610:
596:
593:
592:
585:
549:, the smallest
539:independent set
514:
503:
489:
394:
391:
390:
320:
317:
316:
309:
242:
168:
166:Edge-transitive
164:
160:
156:
152:
117:Chromatic index
17:
12:
11:
5:
1170:
1160:
1159:
1154:
1152:Regular graphs
1149:
1133:
1132:
1093:
1082:(3): 235–238,
1055:
1049:Jessica Wolz,
1042:
1029:
984:
969:
938:Gleason, A. M.
925:
889:
866:
853:
827:
826:
824:
821:
820:
819:
812:
805:
803:
796:
789:
787:
780:
773:
771:
764:
757:
755:
748:
741:
737:
734:
718:arc transitive
699:
695:
669:integral graph
656:
653:
650:
647:
644:
639:
635:
631:
628:
625:
622:
617:
613:
609:
606:
603:
600:
584:
581:
547:Grötzsch graph
512:
501:
496:complete graph
487:
473:book thickness
466:Petersen graph
454:edge-connected
422:
419:
416:
413:
410:
407:
404:
401:
398:
378:
375:
372:
369:
366:
363:
360:
357:
354:
351:
348:
345:
342:
339:
336:
333:
330:
327:
324:
308:
305:
241:
238:
211:Alfred Clebsch
181:
180:
174:
173:
147:
143:
142:
139:
133:
132:
129:
127:Book thickness
123:
122:
119:
113:
112:
109:
103:
102:
99:
93:
92:
89:
83:
82:
79:
73:
72:
69:
63:
62:
59:
53:
52:
49:
43:
42:
40:Alfred Clebsch
37:
33:
32:
24:
23:
15:
9:
6:
4:
3:
2:
1169:
1158:
1155:
1153:
1150:
1148:
1145:
1144:
1142:
1128:
1124:
1119:
1114:
1110:
1106:
1105:
1097:
1089:
1085:
1081:
1077:
1070:
1068:
1059:
1052:
1046:
1039:
1033:
1019:
1018:10.37236/1224
1015:
1011:
1007:
1006:
998:
994:
988:
980:
973:
965:
961:
956:
951:
947:
943:
939:
932:
930:
915:on 2013-10-29
911:
904:
898:
896:
894:
884:
880:
876:
870:
863:
857:
842:
835:
833:
828:
816:
809:
804:
800:
793:
788:
784:
777:
772:
768:
761:
756:
752:
745:
740:
739:
733:
731:
728:. It is also
727:
723:
719:
715:
697:
693:
685:
684:Coxeter group
681:
676:
674:
670:
651:
648:
645:
637:
629:
626:
623:
615:
607:
604:
601:
590:
580:
578:
573:
571:
567:
563:
558:
556:
552:
551:triangle-free
548:
544:
540:
536:
531:
529:
525:
521:
518:
517:Ramsey number
511:
507:
500:
497:
484:
480:
478:
474:
469:
467:
463:
459:
455:
451:
447:
443:
439:
434:
417:
414:
411:
408:
405:
402:
399:
373:
370:
367:
364:
361:
358:
355:
349:
343:
340:
337:
334:
331:
328:
325:
314:
304:
301:
297:
293:
289:
285:
281:
276:
274:
270:
265:
263:
259:
255:
251:
247:
237:
235:
232:
231:Ramsey number
228:
224:
220:
216:
212:
208:
204:
203:regular graph
200:
199:complementary
196:
195:Clebsch graph
192:
188:
179:
175:
171:
167:
163:
159:
155:
151:
148:
144:
140:
138:
134:
130:
128:
124:
120:
118:
114:
110:
108:
104:
100:
98:
97:Automorphisms
94:
90:
88:
84:
80:
78:
74:
70:
68:
64:
60:
58:
54:
50:
48:
44:
41:
38:
34:
30:
25:
22:Clebsch graph
20:
1108:
1102:
1096:
1079:
1075:
1066:
1058:
1050:
1045:
1032:
1021:. Retrieved
1009:
1003:
993:Godsil, C.D.
987:
972:
945:
941:
917:. Retrieved
910:the original
882:
878:
869:
856:
845:. Retrieved
680:Cayley graph
677:
586:
574:
562:Keller graph
559:
555:induced path
532:
527:
519:
509:
498:
493:
477:queue number
470:
464:copy of the
446:non Eulerian
435:
310:
296:half-squares
277:
273:perfect cube
269:finite field
266:
257:
253:
249:
243:
240:Construction
233:
218:
194:
191:graph theory
187:mathematical
184:
158:Cayley graph
137:Queue number
875:Clebsch, A.
751:Hamiltonian
577:regular map
438:Hamiltonian
262:identifying
154:Hamiltonian
36:Named after
1141:Categories
1023:2009-08-13
919:2011-05-21
847:2009-08-13
823:References
570:hypercubes
462:isomorphic
442:non planar
307:Properties
300:isomorphic
284:complement
146:Properties
885:: 142–184
649:−
627:−
344:μ
338:λ
189:field of
1069:(3,3,3)"
995:(1995).
720:, hence
673:spectrum
254:opposite
77:Diameter
47:Vertices
1127:1904597
1088:0765316
964:0067467
948:: 1–7,
736:Gallery
535:colored
471:It has
225: (
185:In the
1125:
1086:
962:
671:: its
475:4 and
456:. The
452:and 5-
193:, the
67:Radius
1072:(PDF)
1012:: 3.
1000:(PDF)
913:(PDF)
906:(PDF)
87:Girth
57:Edges
797:The
781:The
765:The
724:and
587:The
545:the
444:and
227:1955
101:1920
1113:doi
1109:251
1014:doi
950:doi
568:by
479:3.
468:.
1143::
1123:MR
1121:,
1107:,
1084:MR
1080:22
1078:,
1074:,
1008:.
1002:.
960:MR
958:,
944:,
928:^
892:^
883:69
881:,
831:^
638:10
513:16
502:16
488:16
440:,
433:.
406:10
400:16
356:16
275:.
61:40
51:16
1130:.
1115::
1091:.
1067:R
1026:.
1016::
1010:2
967:.
952::
946:7
922:.
887:.
850:.
817:.
753:.
698:5
694:D
655:)
652:5
646:x
643:(
634:)
630:1
624:x
621:(
616:5
612:)
608:3
605:+
602:x
599:(
528:R
520:R
510:K
499:K
486:K
421:)
418:6
415:,
412:6
409:,
403:,
397:(
377:)
374:2
371:,
368:0
365:,
362:5
359:,
353:(
350:=
347:)
341:,
335:,
332:k
329:,
326:v
323:(
258:n
250:n
234:R
172:.
141:3
131:4
121:5
111:4
91:4
81:2
71:2
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.